算額(その1559)
五十一 岩手県一関市西風 西風白山神社 明治18年(1885)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
今有如図
https://w.atwiki.jp/sangaku/pages/311.html
キーワード:円9個,外円,円弧2個
#Julia, #SymPy, #算額, #和算, #数学
外円の中に円弧 2 個,大円 2 個,小円 6 個を容れる。外円の直径が与えられたとき,小円の直径を求めよ。

山村の図には,円弧 2 個がない。山村は,「問」にある二文字を読み飛ばしている。
『今有如図外円径内隔孤容大円径二個小円径六個其外円若干小円径幾何ナルヤ』
外円径内隔孤容,すなわち,外円の中に弧で隔てて◯◯を容れる。
「今有如図」には円弧が描かれている。
この円弧がないと「術」と合わない解(汚い解)しか得られない。
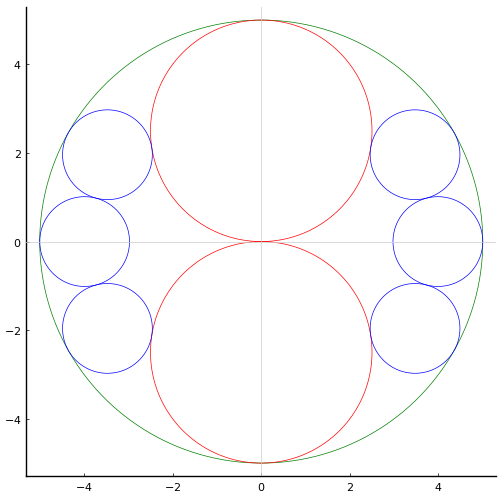
外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, r1); r1 = R/2
小円の半径と中心座標を r2, (R - r1, 0), (x2, y2)
円弧の半径と中心座標を r0, (0, r0)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R::positive, r0::positive, r1::positive,
r2::positive, x2::positive, y2::positive,
x0::positive, y0::positive;
r1 = R/2
eq1 = x2^2 + (r1 - y2)^2 - (r1 + r2)^2
eq2 = x2^2 + y2^2 - (R - r2)^2
eq3 = x2^2 + (r0 - y2)^2 - (r0 - r2)^2
eq4 = (R - r2)^2 + r0^2 - (r0 + r2)^2
eq5 = x0^2 + y0^2 - R^2
eq6 = x0^2 + (r0 - y0)^2 - r0^2
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (r2, x2, y2, r0, x0, y0))[1]
(R/5, 2*sqrt(3)*R/5, 2*R/5, 3*R/2, 2*sqrt(2)*R/3, R/3)
小円の半径 r2 は,外円の半径 R の 1/5 である。
すなわち,外円の直径が 5 寸のとき,小円の直径は 1 寸である。
ちなみに,山村の解釈のように円弧がない場合には,小円同士が外接するようになり,外円の直径が 5 寸のとき,小円の直径は 1.01331 のように半端な数値になり,「算額の対象にするにはみっともない」ことになってしまう。
function draw(R, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = R/2
(r2, x2, y2, r0, x0, y0) = (R/5, 2*sqrt(3)*R/5, 2*R/5, 3*R/2, 2*sqrt(2)*R/3, R/3)
@printf("外円の直径が %g のとき,小円の直径は %g である。\n", 2R, 2r2)
θ = atand(y0 - r0, x0)
plot()
circle(0, r0, r0, :black, beginangle=180 - θ, endangle=360 + θ, n=1000)
circle(0, -r0, r0, :black, beginangle=- θ, endangle=180 + θ, n=1000)
circle(0, 0, R, :green)
circle22(0, r1, r1)
circle4(x2, y2, r2, :blue)
circle2(R - r2, 0, r2, :blue)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
end
end;
draw(5, true)



























