算額(その623)
和算図形問題あれこれ
https://gunmawasan.web.fc2.com/kongetu-no-mondai.html
正方形内に斜線を引き,5 個の等円を並べる。等円の直径が 1 寸のとき,正方形の辺の長さ,斜線の長さはいかほどか。
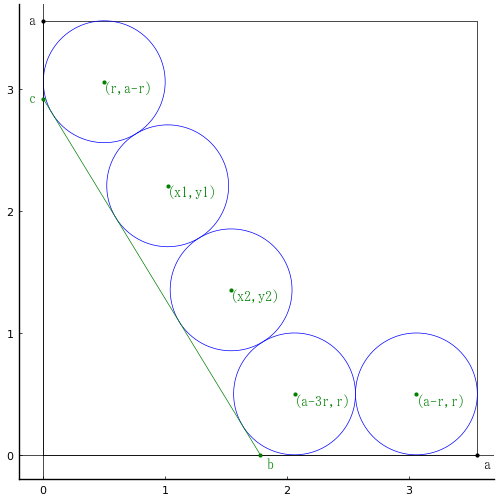
正方形の辺の長さを a, 斜線と正方形の辺の交点座標を (b, 0), (0, c) とおく。
等円の半径と中心座標を r, (r, a - r), (x1, y1), (x2, y2), (a - 3r, r), (a - r, r)
とおき,以下の連立方程式を解く。
なお,中心座標が (r, a - r), (a - 3r, r) の 2 個の等円の中心間の距離についての方程式 (a - 4r)^2 + (a - 2r)^2 = 36r^2 を解けば等円の半径が r のとき,正方形の辺の長さは a = r*(3 + sqrt(17)) であることは容易にわかる。つまり,r = 1/2 なら a = 3.5615528128088303 である。
ただし,このようにして a を求めても b, c は簡単には求まらないし,図を描くときのために (x1, y1), (x2, y2) も求めるとすれば,以下の 7 元連立方程式を解くほうが簡単である。
r = 1/2
r*(3 + sqrt(17))
3.5615528128088303
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms a::positive, b::positive, c::positive, r::positive,
x1::positive, y1::positive, x2::positive, y2::positive
r = 1//2
eq1 = (x1 - r)^2 + (a - r - y1)^2 - 4r^2
eq2 = (x2 - x1)^2 + (y1 - y2)^2 - 4r^2
eq3 = (a - 3r - x2)^2 + (y2 - r)^2 - 4r^2
eq4 = distance(b, 0, 0, c, r, a - r) - r^2
eq5 = distance(b, 0, 0, c, x1, y1) - r^2
eq6 = distance(b, 0, 0, c, x2, y2) - r^2
eq7 = distance(b, 0, 0, c, a - 3r, r) - r^2;
# res = solve([eq2, eq3, eq4, eq5, eq6, eq7], (a, b, c, x1, y1, x2, y2));
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return v, r.f_converged
end;
function H(u)
(a, b, c, x1, y1, x2, y2) = u
return [
(x1 - 1/2)^2 + (a - y1 - 1/2)^2 - 1, # eq1
(-x1 + x2)^2 + (y1 - y2)^2 - 1, # eq2
(y2 - 1/2)^2 + (a - x2 - 3/2)^2 - 1, # eq3
(-b*(-2*a*c + b + 2*c^2 + c)/(2*(b^2 + c^2)) + 1/2)^2 + (a - c*(2*a*c + 2*b^2 - b - c)/(2*(b^2 + c^2)) - 1/2)^2 - 1/4, # eq4
(-b*(b*x1 + c^2 - c*y1)/(b^2 + c^2) + x1)^2 + (-c*(b^2 - b*x1 + c*y1)/(b^2 + c^2) + y1)^2 - 1/4, # eq5
(-b*(b*x2 + c^2 - c*y2)/(b^2 + c^2) + x2)^2 + (-c*(b^2 - b*x2 + c*y2)/(b^2 + c^2) + y2)^2 - 1/4, # eq6
(-c*(-2*a*b + 2*b^2 + 3*b + c)/(2*(b^2 + c^2)) + 1/2)^2 + (a - b*(2*a*b - 3*b + 2*c^2 - c)/(2*(b^2 + c^2)) - 3/2)^2 - 1/4, # eq7
]
end;
r = 1/2
iniv = BigFloat[3.54, 1.71, 2.79, 0.96, 2.14, 1.54, 1.29]
res = nls(H, ini=iniv)
(BigFloat[3.561552812808830274910704927987038512573599612686810217199316786547477173168936, 1.780776406404415137455352463993519256286799806343405108599658393273738586584675, 2.921164609606622706183028695990278884430199709515107662899487589910607879873015, 1.020517604269610091636901642662346170857866537562270072399772262182492391055713, 2.207701875205886849940469951991359008382399741791206811466211191031651448778865, 1.54103520853922018327380328532469234171573307512454014479954452436498478211229, 1.353850937602943424970234975995679504191199870895603405733105595515825724389432], true)
正方形の一辺の長さは 3.56155 寸,斜線の長さは = sqrt(b^2 + c^2) = 3.42116 寸である。
その他のパラメータは以下の通り。
a = 3.56155; b = 1.78078; c = 2.92116; x1 = 1.02052; y1 = 2.2077; x2 = 1.54104; y2 = 1.35385
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 1/2
(a, b, c, x1, y1, x2, y2) = res[1]
斜線 = sqrt(b^2 + c^2)
@printf("正方形の一辺の長さ = %g; 斜線の長さ = %g; a = %g; b = %g; c = %g; x1 = %g; y1 = %g; x2 = %g; y2 = %g\n",
a, 斜線, a, b, c, x1, y1, x2, y2)
plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:black, lw=0.5, xlims=(-0.2, 3.7), ylims=(-0.2, 3.7))
circle(r, a - r, r, :blue)
circle(x1, y1, r, :blue)
circle(x2, y2, r, :blue)
circle(a - 3r, r, r, :blue)
circle(a - r, r, r, :blue)
segment(0, c, b, 0, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
point(r, a - r, "(r,a-r)")
point(x1, y1, "(x1,y1)")
point(x2, y2, "(x2,y2)")
point(a - 3r, r, "(a-3r,r)")
point(a - r, r, "(a-r,r)")
point(a, 0, " a", :black, :left, :top, delta=-delta/2)
point(b, 0, " b", :green, :left, :top, delta=-delta/2)
point(0, a, "a ", :black, :right, :vcenter)
point(0, c, "c ", :green, :right, :vcenter)
end
end;

























※コメント投稿者のブログIDはブログ作成者のみに通知されます