算額(その862)
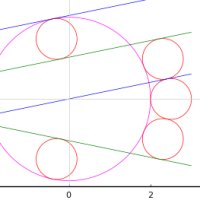
依拠した図が間違っているので,「算額(その862)改訂版」を書いた。
二十六 岩手県一関市萩荘 赤萩観音寺前額 弘化4年(1847)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
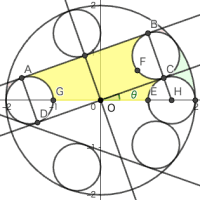
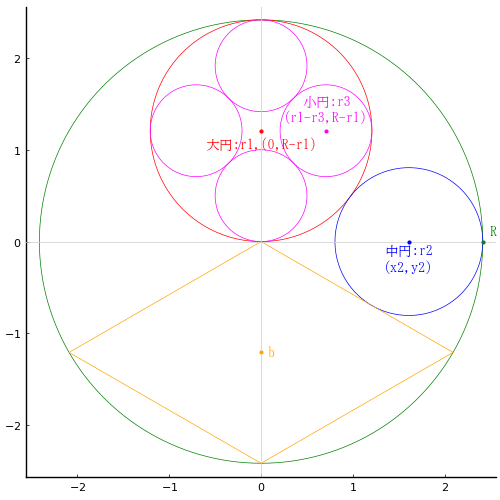
全円内に大円 1 個,中円 2 個,小円 4 個と菱形が入っている。小円の直径を知って,全円の直径を求めよ。注:「中円 4 個,小円 2 個」と書いているが明らかに誤記であろう。いや,図が間違っているのだ。
大円の直径は小円の直径の (1 + √2) 倍である。これを踏まえると,大円と中円と菱形が全円の中に入っているとき,全円の直径を求めよという問題になる。それは,算額(その445)https://blog.goo.ne.jp/r-de-r/e/9f35b3c1b37302b50c61355f43956949 と同じ問題であるが,そこに示したように,描画パラメータは 5 個で,既知のパラメータはそのうちの 2 個,条件は 3 つなので,方程式は解くことができる。しかし,本問では既知の条件は1つしかないので,方程式は解けない。方程式を解くためには既知のパラメータをもう 1 つ見つける必要がある。とはいっても,もっとも単純に「大円の直径が全円の半径に等しい」と仮定する以外の妥当な方策はない。
大円の直径は小円の直径の (1 + √2) 倍なので,全円の直径は小円の直径の 2(1 + √2) ≒ 4.82842712474619 倍である。
術では「全円の直径は小円の直径の 5 倍」としているが,疑問である。
算額の答えはここまでである。
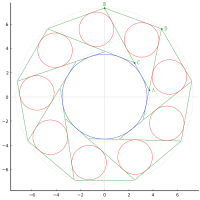
以下では,図を描くために,中円のパラメータを求める。
全円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, R - r1)
中円の半径と中心座標を r2, (x2, y2)
小円の半径と中心座標を r3, (r1 - r3, R - r1)
とおき,以下の連立方程式を解く。
パラメータは以下のとおりである。
r3 = 0.5; r1 = 1.20711; R = 2.41421; r2 = 0.804738; x2 = 1.60948; y2 = 0
include("julia-source.txt");
using SymPy
@syms b::positive, R::positive, r1::positive,
r2::positive, x2::positive, y2,
r3::positive, d
r3 = 1//2
r1 = (1 + √Sym(2))r3
R = 2r1
b = R - r1
eq1 = x2^2 + y2^2 - (R - r2)^2
eq2 = x2^2 + (R - r1 - y2)^2 - (r1 + r2)^2
eq3 = dist(0, 0, sqrt(R^2 - (b - R)^2), b - R, x2, y2) - r2^2
# eq4 = 2(r1 - r3)^2 - 4r3^2
res = solve([eq1, eq2, eq3], (r2, x2, y2))
1-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
(1/3 + sqrt(2)/3, sqrt(8*sqrt(2)/9 + 4/3), 0)
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r3 = 1/2
r1 = (1 + √2)r3
R = 2r1
(r2, x2, y2) = (1/3 + sqrt(2)/3, sqrt(8*sqrt(2)/9 + 4/3), 0)
@printf("r3 = %g; r1 = %g; R = %g; r2 = %g; x2 = %g; y2 = %g\n", r3, r1, R, r2, x2, y2)
b = R - r1
plot()
circle(0, 0, R, :green)
circle(0, R - r1, r1)
circle2(r1 - r3, R - r1, r3, :magenta)
circle(0, R - r3, r3, :magenta)
circle(0, R - 2r1 + r3, r3, :magenta)
circle(x2, y2, r2, :blue)
x = sqrt(R^2 - (b - R)^2)
plot!([0, x, 0, -x, 0], [-R, b - R, 2b -R, b - R, -R], color=:orange, lw=0.5)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(R, 0, " R", :green, :left, :bottom, delta=delta/2)
point(0, R - r1, "大円:r1,(0,R-r1)", :red, :center, delta=-delta)
point(x2, y2, "中円:r2\n(x2,y2)", :blue, :center, delta=-delta/2)
point(r1 - r3, R - r1, "小円:r3\n(r1-r3,R-r1)", :magenta, :center, :bottom, delta=delta)
point(0, b - R, " b", :orange, :left, :vcenter)
end
end;