算額(その314)
(4) 京都府長岡京市天神 長岡天満宮 寛政2年(1970)
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
p02-03 特集「算額」(杉浦).indd
https://www.s-coop.net/lifestage/backnumber/2011/pdf/1106_02-03.pdf
キーワード:円8個,正方形
図のように,大円と小円の間に正方形がある。大円と小円の直径はそれぞれ 5cm, 3cm である。正方形の辺の長さを求めよ。
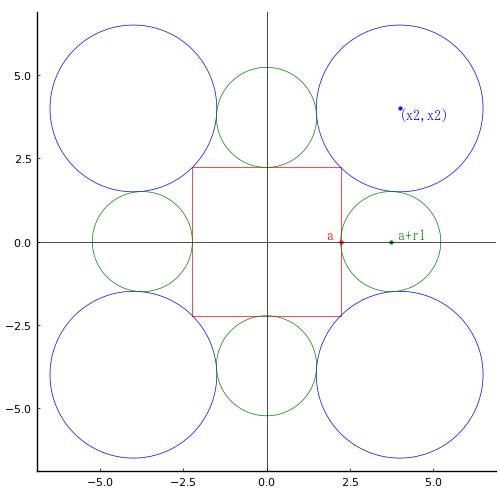
正方形の辺の長さを 2a,右上の大円の中心座標を (x2, x2) とする。右の小円の中心座標を (a + r1, 0) とする。
以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::positive, x2::positive
(r1, r2) = (3/2, 5/2)
eq1 = (x2 - (a + r1))^2 + x2^2 - (r1 + r2)^2
eq2 = (sqrt(2)a + r2)^2 - 2x2^2
res = solve([eq1, eq2], (a, x2))
1-element Vector{Tuple{Sym, Sym}}:
(2.22326059127573, 3.99102754424210)
2res[1][1] |> println
4.44652118255146
正方形の一辺の長さは 2 * 2.22326059127573 = 4.44652118255146 cm
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2) = (3/2, 5/2)
(a, x2) = res[1]
plot()
rect(-a, -a, a, a, :red)
circle4(x2, x2, r2, :blue)
circle42(0, a + r1, r1, :green)
if more
point(a, 0, "a ", :red, :right, :bottom)
point(a + r1, 0, " a+r1", :green, :left, :bottom)
point(x2, x2, "(x2,x2)", :blue)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;



























