考える訓練

算数の問題ができない、というときに原因はいくつか考えられます。

例えば直角三角形の面積を求める問題があったとして、

三角形の面積の公式を知らない

という場合もあるでしょう。

あるいは知っていても、途中で計算間違いをした、という場合もあるかもしれません。

公式を知らない場合は、公式を覚えることが必要だし、ミスをしたのならミスをしない解き方を編み出す必要があります。

公式を知っていて、ていねいに解いていくこともできる子がいたとして、でもこういう問題は解けなかったとしましょう。



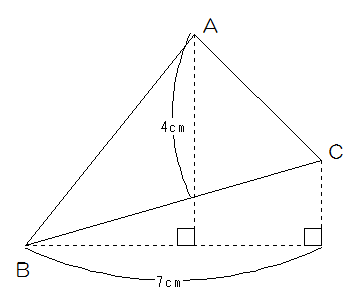
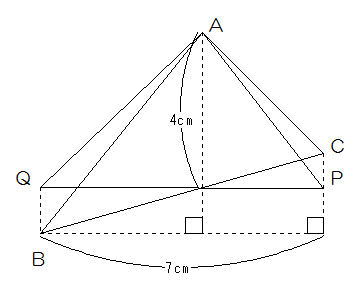
これは底辺をたての線として、２つの三角形に分けたときにその高さの和が7cmになる、とも考えられるし、三角形ABCを下の図のように等積移動させて△APQの面積を求めてもいいかもしれません。



で、三角形の面積の公式を知っていれば、確かに上のように考えられる、ということですが、ある意味こう考えるんだ、という知識としてとらえることもできます。

ただ、これを知識としてとらえてしまうと、本当にたくさんの知識を覚えていないといけないということになるので、これは対策として合理的ではないし、ちょっと条件を変えられるだけで、間違えてしまう可能性もある。

だったら、知識は三角形の面積の公式にとどめておいて、ここからどう考えていくか、考えられる力をつけるのがいい、という話になるわけです。

ところがこの力というのが、案外とらえどころのない話なのであって、いったいどのくらい力がついたかをはかる目安が立ちにくい。先の解法を知識としてとらえれば、100個覚えたとか、200個覚えたとか定量的に学習量をはかることができるかもしれませんが、こういう力は例えばある問題はできて、相変わらずある問題はできない、みたいなところがあるからとらえにくいのです。

だから、どれくらい考える力がついたかを定量的に考えるのはやめた方が良いのです。だって例えば、ある学校の合格確実圏のレベルにまで達していたところで、当日の入試問題ができなければ合格しないのだから、その定量には不確実さがたくさん残っていることになる。

ただ、方法論として「知識として扱うのではなく、考える訓練を積み重ねるのだ」という方向性を持っていればいいだけです。あとは、コツコツ積み上げていって、それこそ「本番で勝負！」ということで良いのではないでしょうか。

確かに親とすれば進行状況が知りたいところではあるし、指導する側にもそういうニーズはあるのだけれど、それは結構不確実なものであるから、あまり数字にこだわらない、とした方が精神衛生上良いと思っています。

=============================================================
今日の田中貴.com

大学付属校と系属校
==============================================================
今日の慶應義塾進学情報

部活は何がやりたい？
==============================================================

==============================================================

「映像教材、これでわかる比と図形」（田中貴）
==============================================================



にほんブログ村