折り紙で卵形の曲面をつくろうとして、インターネットで卵形曲線の方程式を探していたら、山本信雄氏の記事に出会ったので、氏が紹介する方程式を使わせてもらうことにした。
x軸上に置いた点をQ(c,0)とし(cはほぼ任意の定数であろう)、曲線上の点をP(x,y)とするとき、PQとx軸とがつくる角度をシータtとするとき、tを媒介変数とする卵形曲線の方程式は、次のように提示される。
x={a/2-b(1-cost)/4}(1+cost)
y={a/2-b(1-cost)/4}sint
b=0.7aの場合が実際の卵とそっくりという。
Excelで、変数t,x,yの列を設定する。tの列に連続データの作成手順に従って0から2パイ(約6.28)までの間の角度の刻みデータを作成する。xとyの列の各々に上記の式を設定して計算させると、容易に(x,y)のリストを作成できる。
図は、a=4としたときの卵形曲線のグラフである。
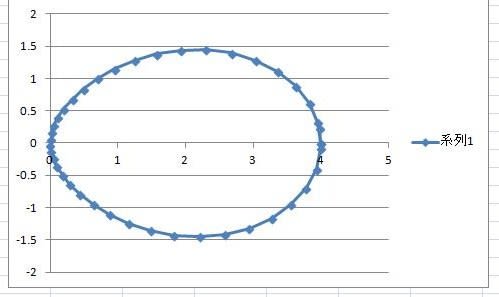
図でx=2の近くに卵形曲線が極大および極小になる点が存在する。この点を含み、曲線を水平な線分で近似できそうな領域を中央分離帯とすると、これより左側の領域は、とがった凸領域のカーブを除いて曲線を斜め方向の線分で近似すると、少なくとも4つのレーンの帯で構成できるだろう。また、分離帯の右側の領域は、丸い凸領域のカーブを除いて曲線を斜め方向の線分で近似すると、少なくとも5つのレーンの帯で構成できるだろう。
左右の凸領域は、各短冊の寸法だけを確保しておいて、フリーハンドで曲面を形成できればよい。
中央分離帯をはじめとする各レーンのリングは、少なくとも18角形で近似する必要があるだろう。そうすると、各レーンの形を形成するためには、18個所の扇形の切り込みが必要である。各切り込み個所の切り込み幅は、各レーン境界の円周サイズから計算できる。
このようにして、一枚の紙で卵形曲面の展開図を作成できるので、展開図を切り抜き、レーン境界と18角形の頂点線分を山折りにし、切り込み部分を貼り合わせ、凸領域を丸めると、卵形曲面のモデルができる。
でき上がった卵形モデルを見ると、卵形というより手榴弾のように見える。できることが分かったので、より卵形らしい丸みをつけるには、各レーンを構成するリングの近似精度を上げればよい。
しかし、18角形の山折りを36角形の近似にするのはより難度が高くなる。18角形の頂点線分の山折りをやめて、中央分離帯をはじめ各レーンが丸みをもつように癖をつけると、より丸みを帯びた卵形モデルができるだろう。
x軸上に置いた点をQ(c,0)とし(cはほぼ任意の定数であろう)、曲線上の点をP(x,y)とするとき、PQとx軸とがつくる角度をシータtとするとき、tを媒介変数とする卵形曲線の方程式は、次のように提示される。
x={a/2-b(1-cost)/4}(1+cost)
y={a/2-b(1-cost)/4}sint
b=0.7aの場合が実際の卵とそっくりという。
Excelで、変数t,x,yの列を設定する。tの列に連続データの作成手順に従って0から2パイ(約6.28)までの間の角度の刻みデータを作成する。xとyの列の各々に上記の式を設定して計算させると、容易に(x,y)のリストを作成できる。
図は、a=4としたときの卵形曲線のグラフである。

図でx=2の近くに卵形曲線が極大および極小になる点が存在する。この点を含み、曲線を水平な線分で近似できそうな領域を中央分離帯とすると、これより左側の領域は、とがった凸領域のカーブを除いて曲線を斜め方向の線分で近似すると、少なくとも4つのレーンの帯で構成できるだろう。また、分離帯の右側の領域は、丸い凸領域のカーブを除いて曲線を斜め方向の線分で近似すると、少なくとも5つのレーンの帯で構成できるだろう。
左右の凸領域は、各短冊の寸法だけを確保しておいて、フリーハンドで曲面を形成できればよい。
中央分離帯をはじめとする各レーンのリングは、少なくとも18角形で近似する必要があるだろう。そうすると、各レーンの形を形成するためには、18個所の扇形の切り込みが必要である。各切り込み個所の切り込み幅は、各レーン境界の円周サイズから計算できる。
このようにして、一枚の紙で卵形曲面の展開図を作成できるので、展開図を切り抜き、レーン境界と18角形の頂点線分を山折りにし、切り込み部分を貼り合わせ、凸領域を丸めると、卵形曲面のモデルができる。
でき上がった卵形モデルを見ると、卵形というより手榴弾のように見える。できることが分かったので、より卵形らしい丸みをつけるには、各レーンを構成するリングの近似精度を上げればよい。
しかし、18角形の山折りを36角形の近似にするのはより難度が高くなる。18角形の頂点線分の山折りをやめて、中央分離帯をはじめ各レーンが丸みをもつように癖をつけると、より丸みを帯びた卵形モデルができるだろう。









