4次元空間の中にワームホールのモデルをつくる

　3次元空間内にある曲線や曲面を示す図形は、座標(x,y,z)を用いて関数f(x,y,z)=0の形式の方程式で表現できる。

　同様に、4次元空間内の図形は、座標(x,y,z,w)を用いて関数f(x,y,z,w)=0の形式の方程式で表現できる。

　図は、我々の3次元宇宙と別の3次元宇宙を連結するワームホールのモデルを示す。ワームホールは、4次元空間の中に存在するとされる仮説上の空間領域である。我々の宇宙は4次元空間のw=0に位置し、別の宇宙はw=3に位置する。



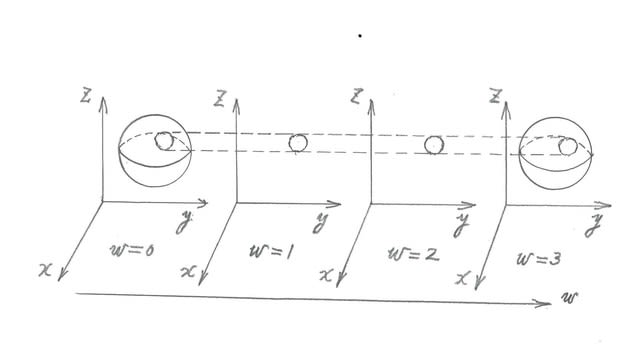
　我々の宇宙のモデルは、x^2+y^2+z^2=1の方程式で表される球面の内側の面に存在する。ただし、y>0かつx^2+z^2=<1-c^2の領域には宇宙は存在せず、宇宙はこの領域を除く球内面の全領域ということになる。ここで、y>0かつx^2+z^2=1-c^2は、球面x^2+y^2+z^2=1と平面y=cの交わりたる円の方程式である。cは0.9程度の定数である。

　0
　0<w<3に存在するすべての円周の集合は、円柱の側面ということになる。つまり、その内側の面はワームホールと呼ばれるチューブを形成する。

　別の宇宙のモデルもx^2+y^2+z^2=1の方程式で表される球面の内側の面に存在する。ただし、y<0かつx^2+z^2=<1-c^2の領域には宇宙は存在せず、宇宙はこの領域を除く球内面の全領域ということになる。

　我々の宇宙モデルからy>cの領域に足を踏み入れたとき、4次元空間のw>0の領域、つまりワームホールに入る。

　Wが増大する方向にワームホールを進み、w=3の領域に入ると、別の宇宙モデルに到着する。

　このような宇宙モデルは、3次元空間内だけでも構成できるとする意見があるかも知れない。しかし、4次元空間を使うと、変数wがどう変化しても一連の3次元空間内の図形が同一の座標(x,y,z)に基づく方程式で表現できる。

　参考文献
　小笠英志著「異次元への扉」(日本評論社)

バーバーの「弦楽のためのアダージョ」を聴く

　弦楽合奏団の演奏会があったので、出かけて行き、首記の曲の演奏を聴いた。

　この曲を聴いていて、ふとこれは20世紀の「G線上のアリア」ではなかろうかという感慨を覚えた。

　敬虔なキリスト教信者であったバッハは、自分の作品を神に捧げることを意識しながら作曲したようだ。

　バッハのニ長調の優美な曲に比べてバーバーのこの曲は、悲しみと憂いに満ち溢れている。

　神が死んだとも言われる20世紀には、2度の世界大戦が起き、膨大な数の死傷者とともに多くの悲劇を生んだ。首記の曲は、これら戦争による悲劇を象徴しているように聞こえる。あるいは戦死者への鎮魂を意図しているかのように聞こえる。

　ここまで書いてきて、音楽の素人が言う戯言ではないだろうかという疑問が生じてきた。国語辞典によれば、「アリア」とは、「歌劇、(オラトリオ、カンタータ)などの抒情的なメロディを主とした独唱。詠唱。」とある。バーバーのこの弦楽合奏曲とは関係ないようにみえる。しかし、解説書によると、この曲は、後年「アニュス・デイ」という宗教的合唱曲に編曲されているそうだ。両者は、宗教的色彩をもつ歌曲という共通点をもつのであれば無関係とは思えない。

　私の説がこじつけであることを自覚しながらこのブログを書いている。