今年のノーベル物理学賞は、量子力学にトポロジー(位相幾何学)の概念を導入した米国の研究者に贈られた。この業績についてサイエンス・コミュニケーション向けの説明をしたいが、いきなりトポロジー+量子力学+物性というテーマに取り組むのは難度が高すぎる。
そこで、高度なテーマに進む前に、トポロジー+古典力学程度から始めるのがよいのではないかと考えていた。以前に新聞に出ていた数学者の砂田利一さんの「最小作用の原理とトポロジーを組み合わせることによりダイヤモンドの結晶構造を説明する例」のことを思い出したので、まずこれをテーマにして問題に取り組むことにした。
ダイヤモンドの結晶は、炭素原子が規則正しく配列したものであるが、熱振動により結晶構造が変形する。三次元空間上の単位格子として、8つの原子が各々を頂点とする平行六面体をつくると考えると、変形したすべての六面体は、トポロジーで言う多様体の一つであって、位相的に同型であり、一つの六面体から別の六面体へは連続変形により移ることができる。各々の単位格子にはそのエネルギーを表す微分可能な関数を付着させることができる。このエネルギー値を最小にするような形の単位格子の集まりが安定な結晶構造をつくると考えることができる。
三次元空間上の単位格子の形を想像することは難しいので、これを簡略化したものとして、まず二次元平面上の単位格子が図に示すような等辺の平行四辺形であるような格子構造を考える。この平行四辺形の各頂点(格子点)には各々の原子がその位置を占めている。
今年のノーベル物理学賞は、量子力学にトポロジー(位相幾何学)の概念を導入した米国の研究者に贈られた。この業績についてサイエンス・コミュニケーション向けの説明をしたいが、いきなりトポロジー+量子力学+物性というテーマに取り組むのは難度が高すぎる。
そこで、高度なテーマに進む前に、トポロジー+古典力学程度から始めるのがよいのではないかと考えていた。以前に新聞に出ていた数学者の砂田利一さんの「最小作用の原理とトポロジーを組み合わせることによりダイヤモンドの結晶構造を説明する例」のことを思い出したので、まずこれをテーマにして問題に取り組むことにした。
ダイヤモンドの結晶は、炭素原子が規則正しく配列したものであるが、熱振動により結晶構造が変形する。三次元空間上の単位格子として、8つの原子が各々を頂点とする平行六面体をつくると考えると、変形したすべての六面体は、トポロジーで言う多様体の一つであって、位相的に同型であり、一つの六面体から別の六面体へは連続変形により移ることができる。各々の単位格子にはそのエネルギーを表す微分可能な関数を付着させることができる。このエネルギー値を最小にするような形の単位格子の集まりが安定な結晶構造をつくると考えることができる。
三次元空間上の単位格子の形を想像することは難しいので、これを簡略化したものとして、まず二次元平面上の単位格子が図に示すような等辺の平行四辺形であるような格子構造を考える。この平行四辺形の各頂点(格子点)には各々の原子がその位置を占めている。
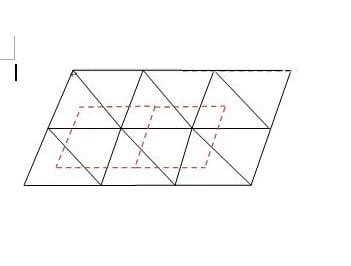
この平行四辺形は、2つの正三角形に分割できる。この正三角形の重心は、正三角形の3つの頂点から同じ距離にある点である。隣接する4つの重心を直線で結ぶと等辺の平行四辺形ができるが、この平行四辺形は、元の平行四辺形と合同である。そうすると、元の平行四辺形の頂点の代わりにこの重心の位置に原子があると考えても問題ないことになる。
この考えは、三次元空間上の平行六面体にも拡張できるだろう。すなわち、この平行六面体はいくつかの正四面体に分割できるだろう。この正四面体についても、その重心を定義することができる。そして、隣接する8つの重心を直線で結ぶと、平行六面体ができるのではないかと想像する。
この考えを確かめるために、厚紙で同じサイズの正四面体を20個つくり、これら正四面体を組み合わせて正二十面体をつくった。20個の正四面体のうち、等間隔の8つの四面体を選び、各々の重心の近くの正三角形に印をつけてみると、8つの重心が平行六面体をつくることが読みとれる。正二十面体は球対称のようにみえるが、さらに多くの正四面体を組み合わせるとすれば、任意の原子を通る独立した3本の座標軸(x,y,z軸)上に原子が配列される格子構造を想像できる。
各格子点に配置される原子の運動を長期的にみると、すべて同等と考えてよいから、単位格子のエネルギー、ひいては結晶全体がもつエネルギーは、一つの原子のエネルギー値で代表される。
ある原子の安定点の位置を原点Oにとり、x軸上に隣接する2つの原子とは各々バネによって結合されているようなモデルを考える。y軸上およびz軸上に隣接する各々2つの原子とも同様にバネによって結合されている。
注目する原子が安定点Oからx軸方向にxだけずれたとき、バネによって原子に働く力が-kx(kはバネ定数)とすると、原子のもつポテンシャル・エネルギーは(k/2)x^2となる(^はべき乗を表す)。x=0のときのポテンシャル・エネルギーを0にとっている。xが微小量ならデルタxをdxと書くことにして、(k/2)dx^2となる。
同様に、y軸方向、z軸方向に働く力は、各々-ky,-kzであるから、y,zの微小量を各々dy,dzと書けば、原子のもつポテンシャル・エネルギー全体の変化dUは、
dU=(k/2)(dx^2+dy^2+dz^2)
となる。こう書くと、dUは、U(dx,dy,dz)とU(0,0,0)との差分だけを意味することになる。dx^2+dy^2+dz^2は、原点Oと原子との間の距離の二乗を示す。言い換えれば、原子の位置を極座標で表すとき、これは動径方向の微小成分の二乗dr^2を表すことになる。
x,y,z軸が互いに直交せず、斜めに傾いていても上記dUの式は成り立つ。x成分、y成分、z成分が互いに独立してさえいればよいことを知る。
こうしてみると、原子にはポテンシャル・エネルギーが最小になる安定点があり、この安定点からいずれかの方向にずれたとき、原子にバネの復元力のような力が働き、安定点に戻すよう作用する。
一般に、原子と原子とが近づきすぎるとき斥力が働き、離れすぎるとき引力が働くというようにファンデルワールス力が働く。そうすると、原子と原子とが適当な距離にあるとき、この力から導かれるエネルギー関数が最小になると考えてよい。このエネルギー関数とバネ力から導かれるエネルギー関数とは異なるが、関数の形がどう変化しても値が最小になる安定点をもつという共通の特徴を有する。ファンデルワールス力をバネ結合された原子のモデルに置き換えても、コトの本質を見失うことにはならない。
参考文献
野口宏著「トポロジー」(日本評論社)
笹田義夫ほか著「結晶の分子科学入門」(講談社サイエンティフィク)
そこで、高度なテーマに進む前に、トポロジー+古典力学程度から始めるのがよいのではないかと考えていた。以前に新聞に出ていた数学者の砂田利一さんの「最小作用の原理とトポロジーを組み合わせることによりダイヤモンドの結晶構造を説明する例」のことを思い出したので、まずこれをテーマにして問題に取り組むことにした。
ダイヤモンドの結晶は、炭素原子が規則正しく配列したものであるが、熱振動により結晶構造が変形する。三次元空間上の単位格子として、8つの原子が各々を頂点とする平行六面体をつくると考えると、変形したすべての六面体は、トポロジーで言う多様体の一つであって、位相的に同型であり、一つの六面体から別の六面体へは連続変形により移ることができる。各々の単位格子にはそのエネルギーを表す微分可能な関数を付着させることができる。このエネルギー値を最小にするような形の単位格子の集まりが安定な結晶構造をつくると考えることができる。
三次元空間上の単位格子の形を想像することは難しいので、これを簡略化したものとして、まず二次元平面上の単位格子が図に示すような等辺の平行四辺形であるような格子構造を考える。この平行四辺形の各頂点(格子点)には各々の原子がその位置を占めている。
今年のノーベル物理学賞は、量子力学にトポロジー(位相幾何学)の概念を導入した米国の研究者に贈られた。この業績についてサイエンス・コミュニケーション向けの説明をしたいが、いきなりトポロジー+量子力学+物性というテーマに取り組むのは難度が高すぎる。
そこで、高度なテーマに進む前に、トポロジー+古典力学程度から始めるのがよいのではないかと考えていた。以前に新聞に出ていた数学者の砂田利一さんの「最小作用の原理とトポロジーを組み合わせることによりダイヤモンドの結晶構造を説明する例」のことを思い出したので、まずこれをテーマにして問題に取り組むことにした。
ダイヤモンドの結晶は、炭素原子が規則正しく配列したものであるが、熱振動により結晶構造が変形する。三次元空間上の単位格子として、8つの原子が各々を頂点とする平行六面体をつくると考えると、変形したすべての六面体は、トポロジーで言う多様体の一つであって、位相的に同型であり、一つの六面体から別の六面体へは連続変形により移ることができる。各々の単位格子にはそのエネルギーを表す微分可能な関数を付着させることができる。このエネルギー値を最小にするような形の単位格子の集まりが安定な結晶構造をつくると考えることができる。
三次元空間上の単位格子の形を想像することは難しいので、これを簡略化したものとして、まず二次元平面上の単位格子が図に示すような等辺の平行四辺形であるような格子構造を考える。この平行四辺形の各頂点(格子点)には各々の原子がその位置を占めている。

この平行四辺形は、2つの正三角形に分割できる。この正三角形の重心は、正三角形の3つの頂点から同じ距離にある点である。隣接する4つの重心を直線で結ぶと等辺の平行四辺形ができるが、この平行四辺形は、元の平行四辺形と合同である。そうすると、元の平行四辺形の頂点の代わりにこの重心の位置に原子があると考えても問題ないことになる。
この考えは、三次元空間上の平行六面体にも拡張できるだろう。すなわち、この平行六面体はいくつかの正四面体に分割できるだろう。この正四面体についても、その重心を定義することができる。そして、隣接する8つの重心を直線で結ぶと、平行六面体ができるのではないかと想像する。
この考えを確かめるために、厚紙で同じサイズの正四面体を20個つくり、これら正四面体を組み合わせて正二十面体をつくった。20個の正四面体のうち、等間隔の8つの四面体を選び、各々の重心の近くの正三角形に印をつけてみると、8つの重心が平行六面体をつくることが読みとれる。正二十面体は球対称のようにみえるが、さらに多くの正四面体を組み合わせるとすれば、任意の原子を通る独立した3本の座標軸(x,y,z軸)上に原子が配列される格子構造を想像できる。
各格子点に配置される原子の運動を長期的にみると、すべて同等と考えてよいから、単位格子のエネルギー、ひいては結晶全体がもつエネルギーは、一つの原子のエネルギー値で代表される。
ある原子の安定点の位置を原点Oにとり、x軸上に隣接する2つの原子とは各々バネによって結合されているようなモデルを考える。y軸上およびz軸上に隣接する各々2つの原子とも同様にバネによって結合されている。
注目する原子が安定点Oからx軸方向にxだけずれたとき、バネによって原子に働く力が-kx(kはバネ定数)とすると、原子のもつポテンシャル・エネルギーは(k/2)x^2となる(^はべき乗を表す)。x=0のときのポテンシャル・エネルギーを0にとっている。xが微小量ならデルタxをdxと書くことにして、(k/2)dx^2となる。
同様に、y軸方向、z軸方向に働く力は、各々-ky,-kzであるから、y,zの微小量を各々dy,dzと書けば、原子のもつポテンシャル・エネルギー全体の変化dUは、
dU=(k/2)(dx^2+dy^2+dz^2)
となる。こう書くと、dUは、U(dx,dy,dz)とU(0,0,0)との差分だけを意味することになる。dx^2+dy^2+dz^2は、原点Oと原子との間の距離の二乗を示す。言い換えれば、原子の位置を極座標で表すとき、これは動径方向の微小成分の二乗dr^2を表すことになる。
x,y,z軸が互いに直交せず、斜めに傾いていても上記dUの式は成り立つ。x成分、y成分、z成分が互いに独立してさえいればよいことを知る。
こうしてみると、原子にはポテンシャル・エネルギーが最小になる安定点があり、この安定点からいずれかの方向にずれたとき、原子にバネの復元力のような力が働き、安定点に戻すよう作用する。
一般に、原子と原子とが近づきすぎるとき斥力が働き、離れすぎるとき引力が働くというようにファンデルワールス力が働く。そうすると、原子と原子とが適当な距離にあるとき、この力から導かれるエネルギー関数が最小になると考えてよい。このエネルギー関数とバネ力から導かれるエネルギー関数とは異なるが、関数の形がどう変化しても値が最小になる安定点をもつという共通の特徴を有する。ファンデルワールス力をバネ結合された原子のモデルに置き換えても、コトの本質を見失うことにはならない。
参考文献
野口宏著「トポロジー」(日本評論社)
笹田義夫ほか著「結晶の分子科学入門」(講談社サイエンティフィク)









