先月にオンライン開催された自然科学カフェに参加し、東京大学の市橋伯一先生の「つくってわかる「生命とは何か」」と題する講演を聴講した。
先生は、大腸菌などの生命体のRNAを編集して、生命体が自己を複製するために必要なタンパク質だけをつくって複製できるようにした人工細胞をつくり、この人工生命が増殖する様子を観察した。
その途中経過の説明は省略することにし、ここでは本ブログと関連する部分―宿主と寄生体との共存関係―についていくらか詳細に説明させてもらいます。
先生は、このRNAをもつ人工生命群の中にRNAの断片を加えてみた。RNA断片とはどういうものか具体的には分からないが、おそらくこの生命体を宿主とするウィルスのような寄生体であろう。
その結果、寄生体が増殖して数が増えると、宿主に悪さをするためか宿主の数が減っていく。しかし、宿主の数が減ると、寄生体の寄生環境が悪くなっていくので、一定の時間遅れを伴って寄生体の数も減っていく。寄生体の数が減ると、宿主の生存環境が良くなるので復活し、再び宿主の数が増えていく。それに伴って寄生体の数も時間遅れで増えていく。
つまり、宿主と寄生体は共存関係にあり、各々の個体数は上がり下がりの振動を繰り返す。宿主と寄生体の共存関係が安定して継続すると、宿主RNAは多様化し、その機能が増えていくとのことである。宿主RNAは寄生体がいないと進化しないというわけである。
ここで、この生命体はどのように進化したのか具体的な説明はなかった。今となってはカフェの場で質問しなかったことが悔やまれる。一種の免疫抗体の生成ではなかろうかと想像するが、これ以上深入りしない。とにかく生命体は、RNA上の遺伝コードを自分で変更して進化プロセスを実行するような「自己組織化」を行ったと考えて間違いないだろう。
以下、本ブログの本題に入ることにし、先生が示唆されたキツネ(捕食者)とウサギ(獲物)が共存するような個体群生態系における個体数の変動状況の数値シミュレーションについて語る。
ウサギの個体群と、それを獲物とするキツネの個体群があるとする。ウサギは、速く増殖するので、自己触媒的である。よく獲物を食べたキツネも増加するが、それは、まわりに充分な数のウサギがいるときに限る。以上より、時とともに捕食者と獲物の個体数がどう変化するかを記述する方程式を書くことができる。
充分な草があるとウサギが増え、ウサギとキツネがいるとキツネが増え、キツネがいると死ぬキツネが出てくる。このプロセスに含まれる3つのステップの相対速度がある範囲におさまっていれば、この生態系はキツネとウサギの数の規則的な周期変動を起こし、キツネの個体数のピークはほぼ完璧にウサギとずれることになる。
このプロセスは、まさに持続する化学的な振動反応に対応している。化合物A(草)と化合物X(ウサギ)が反応すると、Xが増える(自己触媒作用が起こる)とする。これは、
1. A+X--->もっと多くのX(反応速度定数をk1とする)
と書ける。ステップ2では、Xは化合物Y(キツネ)と反応し、さらにYをつくる(これも自己触媒作用である)。
2. X+Y--->もっと多くのY(同定数をk2とする)
最後に化合物Yは自然発生的に崩壊して別の化合物B(死んだキツネ)になる。
3. Y--->B(同定数をk3とする)
このプロセスは、ウサギとキツネの場合と同様に反応物XおよびYの濃度に周期的変動を生じさせる。死んだキツネをカウントするのに、なぜキツネに食われずに死んだウサギをカウントしないのかという疑問が生じるかも知れない。ウサギは増殖が速いので、ウサギの個体数は、出生数から死亡数を引いた正味の個体数でカウントするのであろう。
化合物XとYの濃度をそれぞれxとyとすれば、xとyの変動状況は次の連立する非線形微分方程式で表される。
dx/dt=ak1x-k2xy (1)
dy/dt=k2xy-k3y (2)
ここで、Aが多量にあると仮定し、aを一定とする。
もしウサギが増殖するだけでキツネがいなければ、(1)式はdx/dt=kxの形となり、自己触媒によりバクテリアが増殖するときの式と同じ線形方程式となる。市橋先生の寄生体がいない人工生命の増殖の場合も同じ形式の式となるのであろう。ウサギやバクテリアの食料となる草や栄養物が枯渇するなど増殖が阻害される要因が生じると、(1)式はdx/dt=ax(k-x)の形の非線形のロジスティック方程式で表される。例えば、新型コロナウイルス感染者数の推移状況を表すのに適用可能である。
さて、(1)(2)式の数値計算をするに当たり、dx/dt=0とおくと、xが0でなければy=ak1/k2となるので、xがピーク値になるときのyを初期値y0=ak1/k2に設定する。xとyの近似解をそれぞれx=Acost、xとyの位相差をpとしてy=Bcos(t-p)と仮定して(1),(2)式に代入し、t=0とt=pの場合の式をつくると、ak1,k2,k3,A,B,pを未知数とする連立方程式が得られる。ここでxとyの周期的変動の振動数はSQRT(ak1k3)/2パイになるということなので、この振動数が1になる時間を単位時間にとることにした。A=100に設定し、参考文献の個体数x,yのグラフからBとpを比例配分で求め、ak1とk3の数値を計算し、k2を計算するための式を設定した。
Excelを用いて(1)(2)の計算式を設定し、xとyの時間発展を数値計算した。下図は、ウサギの個体数xとキツネの個体数yの推移を示すグラフである。系列1はx、系列2はyの推移である。
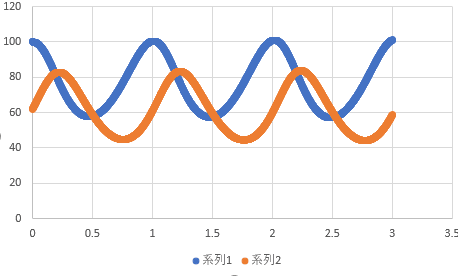
時間の刻み幅dtを大きくとりすぎると、x(t)とy(t)が発散する。できるだけdtを小さくとると、xとyの振幅が一定値に収束していく。本例では、最終的にdt=0.001にとったグラフを示した。
方程式(1)(2)は、x(t)とy(t)の式に変数分離し、各々の変数に関する線形微分方程式で近似できるのかも知れない。
参考文献は、化学反応と個体群生態系とで上記3つのステップは同じと仮定している。そうすると、両者には上記(1)(2)で表される共通の方程式が適用できると考えてよいだろう。しかし、パラメータak1,k2,k3の値の違いによってであろう、参考文献のx,yのグラフを見ると、化学反応型と生態系型で振動パターンが異なるようにみえる。本シミュレーションの結果は、生態系を装いながら化学反応型の振動パターンになっているのかも知れない。市橋先生の人工生命(宿主)と寄生体の共存関係では、各々の個体数の振動パターンは化学反応型になるのだろうか。
参考文献
ボール著「かたち 自然が創り出す美しいパターン」(早川書房)
清水博著「生命を捉えなおす」(中央公論社)
先生は、大腸菌などの生命体のRNAを編集して、生命体が自己を複製するために必要なタンパク質だけをつくって複製できるようにした人工細胞をつくり、この人工生命が増殖する様子を観察した。
その途中経過の説明は省略することにし、ここでは本ブログと関連する部分―宿主と寄生体との共存関係―についていくらか詳細に説明させてもらいます。
先生は、このRNAをもつ人工生命群の中にRNAの断片を加えてみた。RNA断片とはどういうものか具体的には分からないが、おそらくこの生命体を宿主とするウィルスのような寄生体であろう。
その結果、寄生体が増殖して数が増えると、宿主に悪さをするためか宿主の数が減っていく。しかし、宿主の数が減ると、寄生体の寄生環境が悪くなっていくので、一定の時間遅れを伴って寄生体の数も減っていく。寄生体の数が減ると、宿主の生存環境が良くなるので復活し、再び宿主の数が増えていく。それに伴って寄生体の数も時間遅れで増えていく。
つまり、宿主と寄生体は共存関係にあり、各々の個体数は上がり下がりの振動を繰り返す。宿主と寄生体の共存関係が安定して継続すると、宿主RNAは多様化し、その機能が増えていくとのことである。宿主RNAは寄生体がいないと進化しないというわけである。
ここで、この生命体はどのように進化したのか具体的な説明はなかった。今となってはカフェの場で質問しなかったことが悔やまれる。一種の免疫抗体の生成ではなかろうかと想像するが、これ以上深入りしない。とにかく生命体は、RNA上の遺伝コードを自分で変更して進化プロセスを実行するような「自己組織化」を行ったと考えて間違いないだろう。
以下、本ブログの本題に入ることにし、先生が示唆されたキツネ(捕食者)とウサギ(獲物)が共存するような個体群生態系における個体数の変動状況の数値シミュレーションについて語る。
ウサギの個体群と、それを獲物とするキツネの個体群があるとする。ウサギは、速く増殖するので、自己触媒的である。よく獲物を食べたキツネも増加するが、それは、まわりに充分な数のウサギがいるときに限る。以上より、時とともに捕食者と獲物の個体数がどう変化するかを記述する方程式を書くことができる。
充分な草があるとウサギが増え、ウサギとキツネがいるとキツネが増え、キツネがいると死ぬキツネが出てくる。このプロセスに含まれる3つのステップの相対速度がある範囲におさまっていれば、この生態系はキツネとウサギの数の規則的な周期変動を起こし、キツネの個体数のピークはほぼ完璧にウサギとずれることになる。
このプロセスは、まさに持続する化学的な振動反応に対応している。化合物A(草)と化合物X(ウサギ)が反応すると、Xが増える(自己触媒作用が起こる)とする。これは、
1. A+X--->もっと多くのX(反応速度定数をk1とする)
と書ける。ステップ2では、Xは化合物Y(キツネ)と反応し、さらにYをつくる(これも自己触媒作用である)。
2. X+Y--->もっと多くのY(同定数をk2とする)
最後に化合物Yは自然発生的に崩壊して別の化合物B(死んだキツネ)になる。
3. Y--->B(同定数をk3とする)
このプロセスは、ウサギとキツネの場合と同様に反応物XおよびYの濃度に周期的変動を生じさせる。死んだキツネをカウントするのに、なぜキツネに食われずに死んだウサギをカウントしないのかという疑問が生じるかも知れない。ウサギは増殖が速いので、ウサギの個体数は、出生数から死亡数を引いた正味の個体数でカウントするのであろう。
化合物XとYの濃度をそれぞれxとyとすれば、xとyの変動状況は次の連立する非線形微分方程式で表される。
dx/dt=ak1x-k2xy (1)
dy/dt=k2xy-k3y (2)
ここで、Aが多量にあると仮定し、aを一定とする。
もしウサギが増殖するだけでキツネがいなければ、(1)式はdx/dt=kxの形となり、自己触媒によりバクテリアが増殖するときの式と同じ線形方程式となる。市橋先生の寄生体がいない人工生命の増殖の場合も同じ形式の式となるのであろう。ウサギやバクテリアの食料となる草や栄養物が枯渇するなど増殖が阻害される要因が生じると、(1)式はdx/dt=ax(k-x)の形の非線形のロジスティック方程式で表される。例えば、新型コロナウイルス感染者数の推移状況を表すのに適用可能である。
さて、(1)(2)式の数値計算をするに当たり、dx/dt=0とおくと、xが0でなければy=ak1/k2となるので、xがピーク値になるときのyを初期値y0=ak1/k2に設定する。xとyの近似解をそれぞれx=Acost、xとyの位相差をpとしてy=Bcos(t-p)と仮定して(1),(2)式に代入し、t=0とt=pの場合の式をつくると、ak1,k2,k3,A,B,pを未知数とする連立方程式が得られる。ここでxとyの周期的変動の振動数はSQRT(ak1k3)/2パイになるということなので、この振動数が1になる時間を単位時間にとることにした。A=100に設定し、参考文献の個体数x,yのグラフからBとpを比例配分で求め、ak1とk3の数値を計算し、k2を計算するための式を設定した。
Excelを用いて(1)(2)の計算式を設定し、xとyの時間発展を数値計算した。下図は、ウサギの個体数xとキツネの個体数yの推移を示すグラフである。系列1はx、系列2はyの推移である。

時間の刻み幅dtを大きくとりすぎると、x(t)とy(t)が発散する。できるだけdtを小さくとると、xとyの振幅が一定値に収束していく。本例では、最終的にdt=0.001にとったグラフを示した。
方程式(1)(2)は、x(t)とy(t)の式に変数分離し、各々の変数に関する線形微分方程式で近似できるのかも知れない。
参考文献は、化学反応と個体群生態系とで上記3つのステップは同じと仮定している。そうすると、両者には上記(1)(2)で表される共通の方程式が適用できると考えてよいだろう。しかし、パラメータak1,k2,k3の値の違いによってであろう、参考文献のx,yのグラフを見ると、化学反応型と生態系型で振動パターンが異なるようにみえる。本シミュレーションの結果は、生態系を装いながら化学反応型の振動パターンになっているのかも知れない。市橋先生の人工生命(宿主)と寄生体の共存関係では、各々の個体数の振動パターンは化学反応型になるのだろうか。
参考文献
ボール著「かたち 自然が創り出す美しいパターン」(早川書房)
清水博著「生命を捉えなおす」(中央公論社)









