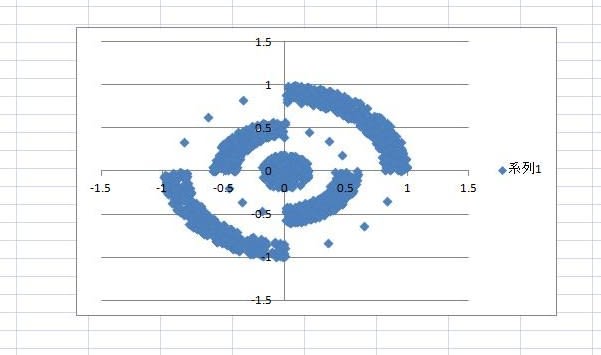
6月10日に「ニューラルネットワークを用いて画像パターンをつくる」のブログを公開した後、そこで紹介した画像パターンの例では何か物足りない感じがつきまとっていた。
Excelの散布図では、微妙な画像パターンを表現できないことが分かったが、点描による画像パターンらしく、点密度の高い領域と点密度がまばらな領域とが共にあるような画像パターンが欲しいと思った。典型的な例を挙げれば、正規分布のように山の頂上付近で点密度が高く、山の裾野の方に下るに従って点密度がまばらになるような画像パターンである。
そこで、Excelの使用を前提とし、正規分布型の画像パターンがどの程度まで可能なのか作図してみることにした。Excelの正規乱数を使えば、正規分布になるような乱数を発生できるという。
半径rが1の円を考える。r<0.2の円領域を空き領域とする。0.2<r<1の領域について外輪領域と内輪領域の面積が等しくなるような分割円周のrを計算すると、r=0.721になる。
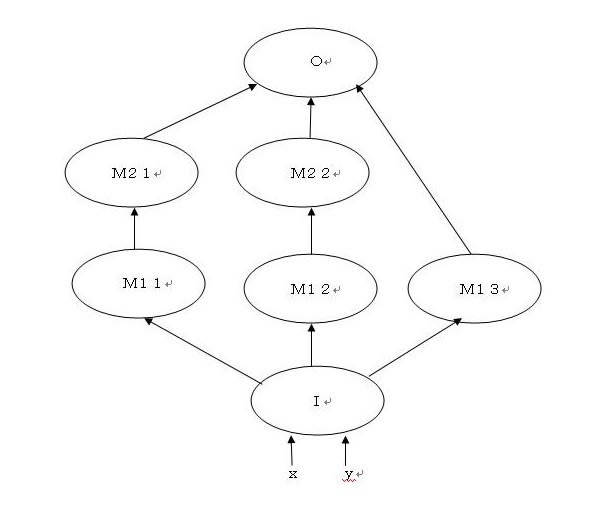
以下、0.2<r<1の範囲のrについて施す処理のステップをニューラルネットワークで表現すると、下図のようになる。
まず、0.2<r<1の範囲の一様乱数を発生させ、入力層のI1とI2のユニットに入力する。I1は、rが0.2<r<0.721の範囲であれば、正規乱数r’を発生させる。正規乱数の平均値は、内輪領域のrの中央値である0.4605である。また、標準偏差シグマは、3シグマが0.721-0.4605になるような値とした。
I2は、rが0.721<r<1の範囲であれば、この範囲の正規乱数r’を発生させる。平均値は、外輪領域のrの中央値である0.8605である。また、標準偏差シグマは、内輪領域のシグマと同じとした。これによって、外輪領域と内輪領域の正規分布は同じ形の関数となる。
第1中間層は、ユニットI1,I2からのデータr’を入力するM11,M12の2つのユニットから成る。M11,M12は、r’に基づいてxの一様乱数を発生させる。xは、(0,0)から(x,y)に達する長さr’のベクトルのx軸と成す偏角(シータt)を媒介変数として表現される。シータtは、M11,M12とは別の列で0<t<2パイの一様乱数として発生させたものである。(2パイは、2*PI()と記述できる)。すなわち、x=r’costで与えられる。
M11は、I1からのデータを入力し、0.2<r’<0.721ならば、上記によるxの一様乱数を出力する。M12は、0.721<r’<1ならばxの一様乱数を出力する。
第2中間層は、ユニットI1,I2からのデータr’を入力し、r’に基づいてyの一様乱数を発生させるM21,M22の2つのユニットから成る。yはy=r’sintで与えられる。ここでシータtはM11またはM12で参照した同じtを参照する。M21は0.2<r’<0.721、M22は0.721<r’<1の条件がつく。
第3中間層は、第1中間層と第2中間層のデータを参照するM31,M32の2つのユニットから成る。M31は、M11,M21の両データが0でなければ1を出力する。M32は、M12,M22の両データが0でなければ2を出力する。
なお、関数によって発生させた一様乱数と正規乱数は、その値を貼り付けて固定した上で参照している。
出力層Oは、選択された(x,y)の値を出力する。すなわち、xとしてM31が1ならM11を出力、1でなければM32が2であるからM12を出力する。また、yとしてM31が1ならM21を出力、1でなければM32が2であるからM22を出力する。
下図は、Excelを用いて上記ニューラルネットワークを表形式に展開し、計算した結果である。
内輪山と外輪山の点密度を比べると、どうしても内輪山の点密度が高く、外輪山の点密度が低くなる。
入力する一様乱数rの件数を2500件程度にすると、外輪山の尾根がつながるようになるので、r方向に正規分布型と言えるような(x,y)点の分布となる。
図の(x,y)点は、3回の乱数発生を重ねて決まるものであり、大局的には予想通り大数の法則に従うような結果となるが、内輪山や外輪山の裾野が不規則な形になるとともに、単独の点の散らばりが生じるなど、別の乱数発生では二度と再現できない画像パターンとなる。
参考文献
伊庭斉志著「進化計算と深層学習」(オーム社)
Excelの散布図では、微妙な画像パターンを表現できないことが分かったが、点描による画像パターンらしく、点密度の高い領域と点密度がまばらな領域とが共にあるような画像パターンが欲しいと思った。典型的な例を挙げれば、正規分布のように山の頂上付近で点密度が高く、山の裾野の方に下るに従って点密度がまばらになるような画像パターンである。
そこで、Excelの使用を前提とし、正規分布型の画像パターンがどの程度まで可能なのか作図してみることにした。Excelの正規乱数を使えば、正規分布になるような乱数を発生できるという。
半径rが1の円を考える。r<0.2の円領域を空き領域とする。0.2<r<1の領域について外輪領域と内輪領域の面積が等しくなるような分割円周のrを計算すると、r=0.721になる。
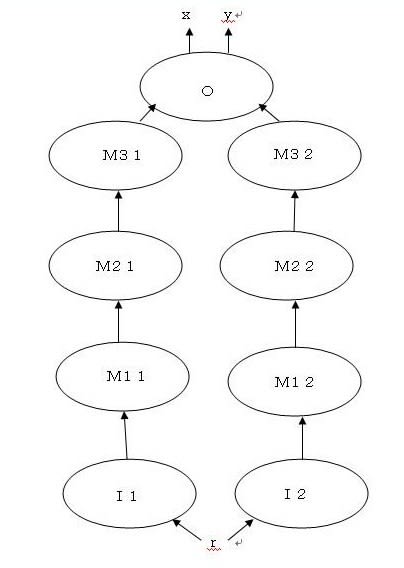
以下、0.2<r<1の範囲のrについて施す処理のステップをニューラルネットワークで表現すると、下図のようになる。

まず、0.2<r<1の範囲の一様乱数を発生させ、入力層のI1とI2のユニットに入力する。I1は、rが0.2<r<0.721の範囲であれば、正規乱数r’を発生させる。正規乱数の平均値は、内輪領域のrの中央値である0.4605である。また、標準偏差シグマは、3シグマが0.721-0.4605になるような値とした。
I2は、rが0.721<r<1の範囲であれば、この範囲の正規乱数r’を発生させる。平均値は、外輪領域のrの中央値である0.8605である。また、標準偏差シグマは、内輪領域のシグマと同じとした。これによって、外輪領域と内輪領域の正規分布は同じ形の関数となる。
第1中間層は、ユニットI1,I2からのデータr’を入力するM11,M12の2つのユニットから成る。M11,M12は、r’に基づいてxの一様乱数を発生させる。xは、(0,0)から(x,y)に達する長さr’のベクトルのx軸と成す偏角(シータt)を媒介変数として表現される。シータtは、M11,M12とは別の列で0<t<2パイの一様乱数として発生させたものである。(2パイは、2*PI()と記述できる)。すなわち、x=r’costで与えられる。
M11は、I1からのデータを入力し、0.2<r’<0.721ならば、上記によるxの一様乱数を出力する。M12は、0.721<r’<1ならばxの一様乱数を出力する。
第2中間層は、ユニットI1,I2からのデータr’を入力し、r’に基づいてyの一様乱数を発生させるM21,M22の2つのユニットから成る。yはy=r’sintで与えられる。ここでシータtはM11またはM12で参照した同じtを参照する。M21は0.2<r’<0.721、M22は0.721<r’<1の条件がつく。
第3中間層は、第1中間層と第2中間層のデータを参照するM31,M32の2つのユニットから成る。M31は、M11,M21の両データが0でなければ1を出力する。M32は、M12,M22の両データが0でなければ2を出力する。
なお、関数によって発生させた一様乱数と正規乱数は、その値を貼り付けて固定した上で参照している。
出力層Oは、選択された(x,y)の値を出力する。すなわち、xとしてM31が1ならM11を出力、1でなければM32が2であるからM12を出力する。また、yとしてM31が1ならM21を出力、1でなければM32が2であるからM22を出力する。
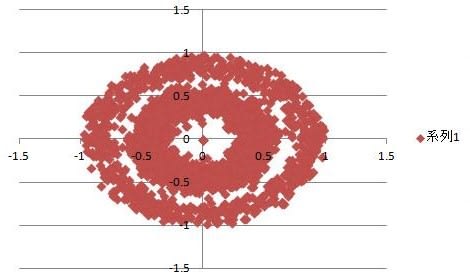
下図は、Excelを用いて上記ニューラルネットワークを表形式に展開し、計算した結果である。

内輪山と外輪山の点密度を比べると、どうしても内輪山の点密度が高く、外輪山の点密度が低くなる。
入力する一様乱数rの件数を2500件程度にすると、外輪山の尾根がつながるようになるので、r方向に正規分布型と言えるような(x,y)点の分布となる。
図の(x,y)点は、3回の乱数発生を重ねて決まるものであり、大局的には予想通り大数の法則に従うような結果となるが、内輪山や外輪山の裾野が不規則な形になるとともに、単独の点の散らばりが生じるなど、別の乱数発生では二度と再現できない画像パターンとなる。
参考文献
伊庭斉志著「進化計算と深層学習」(オーム社)