毎日のように新聞に掲載されていた新型コロナウイルス感染者の累計データを見て、直感的にこのデータには成長曲線のような曲線が当てはまるのではないかと考えていた。
当初、専門家が行った感染者数のシミュレーションの結果を追計算することによって、このシミュレーションの考え方あるいはアルゴリズムを理解できるのではないかと考えた。新聞にはシミュレーションの前提条件や計算結果が公表されていた。
感染者数データに当てはめる曲線として、シグモイド曲線のような指数関数を考えていた。しかし、y=a^xの形の指数関数は、aが0=<a=<1の範囲にあるとき感染者数の増加分または減少分とどう対応するのか不明であり、感染者数の時間発展の関数式を推定するには適切でないことが分かってきた。
その後、数学セミナー2020年5月号の「新型コロナウイルスの数理」という記事を見て、専門家は感染者数の予測に離散的なロジスティック方程式を使っていることを知った。この形式の方程式であれば、指数関数に伴う問題はない。また、ちょうど天気予報のための計算式のように今日の観測データによって計算式のパラメータを修正しながら明日の予測値を計算できるという利点がある。
このテーマについて検討を始めてから3ヶ月ほど経過したが、新型コロナウイルスの蔓延は長期に亘って人々を苦しませ悩ませてきた大きな災害であるから、感染者数の数理について何らかの形で記録を残しておきたい。
感染者数累計yが連続する時刻tの関数y=f(t)であるときのロジスティック方程式は、
dy/dt=ay(k-y) (1)
と書ける。a,kは正数のパラメータである。akyは感染者数の増大を促進する項、-ay^2はそれを抑制する項である。ロジスティック方程式は、生態学の分野でよく知られている方程式のようだ。
dt=1とし、(1)式を離散的なロジスティック方程式に書き直すと、
y(t+1)=y(t)+ay(t)(k-y(t)) (2)
となる。
tはt=0を第0日としたときの第t日を表すとする。第0日は3月1日に相当する。感染者数データを参照すると、感染者数増加のピークはt=41(4月11日)とt=42の間にあるから、t=41.5の時点にあるとみる。実データのy(41)=6000,y(42)=6736であるから、y(41)とy(42)の平均は6368である。(1)式をもう一度tで微分し、dy/dtに(1)の右辺を代入して式の全体を0と置くと、y=0の場合とy=kの場合を除いて、増加がピーク時のy=k/2を得る。そうすると、理論上のy(83)=6368×2=12736、t>83ではy(t)=12736とみてよいだろう。そこで、定数kは12736と置けばよい。
定数aは、
y(42)-y(41)=ay(41)(12736-y(41))=736
によって計算でき、a=0.0000182となる。ここでakを計算すると、0.232となる。
理論上のy(0)は初期値である。初期値は、方程式(2)のy(41)が6000、y(42)が6736に一致するように決めればよい。
Excelを用いて、第t日に対応して各々感染者数データをプロットした。また、第t日に対応して各行に(2)式を設定した。ただし、y(0)には初期値を設定し、t>83のy(t)は12736の一定値を設定した。
y(0)=1とy(0)=2を設定して方程式の計算を試行し、各々y(41)とy(42)の値を見ると、初期値が1と2の間で2に近いところにあることが分かる。そこで、y(41)とy(42)が各々実データに接近するように初期値のきざみ幅を小さくしていくと、y(0)=1.946で両者がともに実データに一致することを知る。初期値の候補を更新するだけで瞬時にy(t)の計算結果が出力表示されるので、Excelは便利である。
以下に実データ(系列1)と計算値(系列2)のグラフを挙げる。
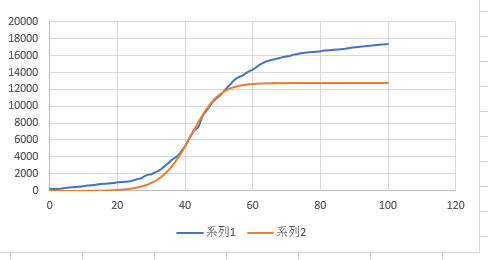
感染者数増加のピーク時附近を除いて実データと計算値とのずれがあり、特にy>kの領域でずれが大きい。y(41)とy(42)では理論値の実データとの誤差が0であったものが、時間の経過とともにその誤差が累積拡大していく様子がみてとれる。
パラメータa,kを日替わりで更新しながらy(t)の予測値を計算すれば精度の高い予測ができるだろう。
参考文献
I.プリゴジンなど著「混沌からの秩序」(みすず書房)
当初、専門家が行った感染者数のシミュレーションの結果を追計算することによって、このシミュレーションの考え方あるいはアルゴリズムを理解できるのではないかと考えた。新聞にはシミュレーションの前提条件や計算結果が公表されていた。
感染者数データに当てはめる曲線として、シグモイド曲線のような指数関数を考えていた。しかし、y=a^xの形の指数関数は、aが0=<a=<1の範囲にあるとき感染者数の増加分または減少分とどう対応するのか不明であり、感染者数の時間発展の関数式を推定するには適切でないことが分かってきた。
その後、数学セミナー2020年5月号の「新型コロナウイルスの数理」という記事を見て、専門家は感染者数の予測に離散的なロジスティック方程式を使っていることを知った。この形式の方程式であれば、指数関数に伴う問題はない。また、ちょうど天気予報のための計算式のように今日の観測データによって計算式のパラメータを修正しながら明日の予測値を計算できるという利点がある。
このテーマについて検討を始めてから3ヶ月ほど経過したが、新型コロナウイルスの蔓延は長期に亘って人々を苦しませ悩ませてきた大きな災害であるから、感染者数の数理について何らかの形で記録を残しておきたい。
感染者数累計yが連続する時刻tの関数y=f(t)であるときのロジスティック方程式は、
dy/dt=ay(k-y) (1)
と書ける。a,kは正数のパラメータである。akyは感染者数の増大を促進する項、-ay^2はそれを抑制する項である。ロジスティック方程式は、生態学の分野でよく知られている方程式のようだ。
dt=1とし、(1)式を離散的なロジスティック方程式に書き直すと、
y(t+1)=y(t)+ay(t)(k-y(t)) (2)
となる。
tはt=0を第0日としたときの第t日を表すとする。第0日は3月1日に相当する。感染者数データを参照すると、感染者数増加のピークはt=41(4月11日)とt=42の間にあるから、t=41.5の時点にあるとみる。実データのy(41)=6000,y(42)=6736であるから、y(41)とy(42)の平均は6368である。(1)式をもう一度tで微分し、dy/dtに(1)の右辺を代入して式の全体を0と置くと、y=0の場合とy=kの場合を除いて、増加がピーク時のy=k/2を得る。そうすると、理論上のy(83)=6368×2=12736、t>83ではy(t)=12736とみてよいだろう。そこで、定数kは12736と置けばよい。
定数aは、
y(42)-y(41)=ay(41)(12736-y(41))=736
によって計算でき、a=0.0000182となる。ここでakを計算すると、0.232となる。
理論上のy(0)は初期値である。初期値は、方程式(2)のy(41)が6000、y(42)が6736に一致するように決めればよい。
Excelを用いて、第t日に対応して各々感染者数データをプロットした。また、第t日に対応して各行に(2)式を設定した。ただし、y(0)には初期値を設定し、t>83のy(t)は12736の一定値を設定した。
y(0)=1とy(0)=2を設定して方程式の計算を試行し、各々y(41)とy(42)の値を見ると、初期値が1と2の間で2に近いところにあることが分かる。そこで、y(41)とy(42)が各々実データに接近するように初期値のきざみ幅を小さくしていくと、y(0)=1.946で両者がともに実データに一致することを知る。初期値の候補を更新するだけで瞬時にy(t)の計算結果が出力表示されるので、Excelは便利である。
以下に実データ(系列1)と計算値(系列2)のグラフを挙げる。

感染者数増加のピーク時附近を除いて実データと計算値とのずれがあり、特にy>kの領域でずれが大きい。y(41)とy(42)では理論値の実データとの誤差が0であったものが、時間の経過とともにその誤差が累積拡大していく様子がみてとれる。
パラメータa,kを日替わりで更新しながらy(t)の予測値を計算すれば精度の高い予測ができるだろう。
参考文献
I.プリゴジンなど著「混沌からの秩序」(みすず書房)









