18年も昔のことであるが、当時のパソコンを使って量子力学の波動方程式の数値計算をしたことがあった。プログラム言語としてはPASCALを使い、調和振動子のいくつかのエネルギー・レベルについて波動関数の数値解を求め、計算結果をグラフ表示した。
参考文献を読んで、ネルソンの確率力学を使えば、波動関数の波形を追うことなく電子の運動経路を計算できることを知った。
自由電子の運動経路を計算するための確率微分方程式のx座標成分は、次のような形式をしている。
X(t+dt)=X(t)+vdt+量子ゆらぎの項 (1)
時間の刻みであるデルタtをdtと書くことにする。vは電子の速度(運動量のx成分/電子の質量)であり、一定である。X(t)は時刻tにおける電子のX座標値、X(t+dt)は時刻t+dtにおける電子のX座標値である。
(1)式の量子ゆらぎの項がなければ、式は古典力学で速度を定義する式:dx/dt=vに他ならない。
量子ゆらぎの項は、ミクロの世界を扱う量子力学のために追加する項であり、定数×A(t)×SQRT(dt)の形をしている。A(t)は、時刻tにおいて、量子ゆらぎによって古典力学の経路から+方向または-方向にずれる確率を与える変数である。SQRT(dt)はdtの平方根を表す。
(1)式の右辺の第2項と第3項は、マクロの世界でニュートンの運動法則が成り立ち、ミクロの世界で量子論が成り立つように、波動関数から導かれたものなので、ネルソンの確率微分方程式は、古典力学と量子力学の両方と整合性をもつものである。
Excelの表にdtの刻みをもつ時間座標を求める式を入力し、確率変数として乱数を求める式を入力し、(1)の計算式を入力し、各々の式を各列の数値になるようにコピーして計算させると、X座標値の列には、時刻t=0でx座標の原点にいた電子がx軸の正方向に自由運動している様子が、時間でdt刻みに計算された位置のx座標の数値の並びとして現れる。
計算結果をグラフ表示してみると、ミクロの世界における自由電子の運動は、一定の速度での等速直線運動に量子力学的不確定性による量子ゆらぎが加わったジグザグ運動となることが分かる。
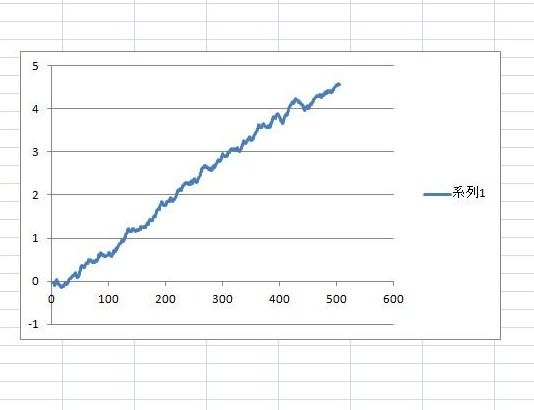
Excelに対して再計算の指示を出すと、乱数の値を変えながら再計算するので、そのたびに計算結果が変わり、各々の見本経路の様子がグラフに現れる。
マクロの世界では物体の質量が極めて大きいため、量子ゆらぎを0と考えて無視することができる。(1)式の量子ゆらぎの項を0にするように変更して計算すると、当然のことながら、古典力学における等速直線運動する質点の運動を示す直線が現れる。
ネルソンの確率力学の手法は、次のような利点をもつ。
まず第一に、古典力学と量子力学とは連続的につながった基本法則であり、両者が無関係に存在する法則ではないことを理解できる。
第二に、量子の位置とその運動量の不確定性を示す量子ゆらぎとはどういうものか目に見える形で表示できる。
第三の利点は、波動関数の重ね合わせに関するものである。自由電子は運動状態の重ね合わせが可能であるから、x軸方向に運動量pで自由運動する場合の波動関数1と同方向に-pで自由運動する場合の波動関数2の重ね合わせであるa×波動関数1+b×波動関数2を波動関数とする運動状態も存在する(a,bは各重みを示す)。
例えばa,b=1のように波動関数1と波動関数2を同じ重みで重ね合わせた波動関数の確率微分方程式をつくり、その計算結果をグラフで表示すると、量子力学的不確定性による小刻みな量子ゆらぎを示すが、ほぼ静止した運動となる。
ミクロの世界での重ね合わせの運動についての見本経路を拡大してグラフ表示してみる。何度か再計算するうちに、初期値であるx軸原点の近くで量子ゆらぎを示していたジグザグの運動経路が、途中の時点から瞬間的にx軸上の正点から負点のように反対符号の点に飛び移り、その後はしばらくその点の近くで量子ゆらぎを示すジグザグ運動を続けるような見本経路が現れる。
重ね合わせた波動関数に関するコペンハーゲン解釈は、電子が波動関数1の運動をしているか、あるいは波動関数2の運動をしているかを観測した場合、確率1/2で波動関数1の運動が観測され、確率1/2で波動関数2の運動が観測されるということしか教えない。この現象は、「波動関数の収縮」とよばれているが、そのメカニズムが明らかでない。
しかし、確率力学による電子の見本経路を見れば、それはただ電子の連続的な運動に伴う量子ゆらぎを意味しているのであって、観測によって波動関数が収縮するわけではないことが分かる。
一方、波動方程式を解いて波動関数を求めるかあるいは波動関数の数値解を計算する手法と比べて、一般に確率力学が不利となるケースが少なくないようにみえる。確率力学は、波動関数に依存しているので、波動関数が求まらなければ、(1)式のような確率微分方程式がつくれない。従って、波動関数が求まらず、その数値解を計算しなければならないケースには対応できないことが想定される。
Excelを使う確率微分方程式の計算では、量子ゆらぎの確率変数A(t)として、RAND()-0.5のような式を与えている。RAND()は0~1の範囲の一様乱数を生成する関数なので、この式は=-0.5~0.5の範囲の一様乱数を与える。
ゆらぎとは平均からのランダムなずれであるとするとき、ゆらぎは中心極限定理という確率法則に従い、ゆらぎの量は正規分布という確率分布によって与えられることが知られている。つまり、この確率分布こそ正規乱数とされる。
参考文献によれば、Excelが用意する乱数は一様乱数であるから、RAND()関数を12回足し合わせたものから6を引いた計算式によって確率変数A(t)を与えるのがよいとする。
実際に参考文献が勧める乱数の計算式によってA(t)を与えてみると、-0.5~0.5の範囲から外れる乱数が多く、計算結果の変動が激しくなり、不安定である。一様乱数を足し合わせるだけで正規乱数の準備ができるという話は疑問である。
古典力学から量子力学への遷移は連続的であることを基本法則とするのであれば、確率変数A(t)は正規乱数でなければならないことになる。特に、粒子の質量が量子のそれから次第に大きくなっていっても運動量保存則が常に成り立つものとすれば、粒子の質量が大きくなるに従って量子ゆらぎが小さくなるであろうから。
参考文献
保江邦夫著「Excelで学ぶ量子力学」(ブルーバックス)
蔵本由紀著「非線形科学」(集英社新書)
参考文献を読んで、ネルソンの確率力学を使えば、波動関数の波形を追うことなく電子の運動経路を計算できることを知った。
自由電子の運動経路を計算するための確率微分方程式のx座標成分は、次のような形式をしている。
X(t+dt)=X(t)+vdt+量子ゆらぎの項 (1)
時間の刻みであるデルタtをdtと書くことにする。vは電子の速度(運動量のx成分/電子の質量)であり、一定である。X(t)は時刻tにおける電子のX座標値、X(t+dt)は時刻t+dtにおける電子のX座標値である。
(1)式の量子ゆらぎの項がなければ、式は古典力学で速度を定義する式:dx/dt=vに他ならない。
量子ゆらぎの項は、ミクロの世界を扱う量子力学のために追加する項であり、定数×A(t)×SQRT(dt)の形をしている。A(t)は、時刻tにおいて、量子ゆらぎによって古典力学の経路から+方向または-方向にずれる確率を与える変数である。SQRT(dt)はdtの平方根を表す。
(1)式の右辺の第2項と第3項は、マクロの世界でニュートンの運動法則が成り立ち、ミクロの世界で量子論が成り立つように、波動関数から導かれたものなので、ネルソンの確率微分方程式は、古典力学と量子力学の両方と整合性をもつものである。
Excelの表にdtの刻みをもつ時間座標を求める式を入力し、確率変数として乱数を求める式を入力し、(1)の計算式を入力し、各々の式を各列の数値になるようにコピーして計算させると、X座標値の列には、時刻t=0でx座標の原点にいた電子がx軸の正方向に自由運動している様子が、時間でdt刻みに計算された位置のx座標の数値の並びとして現れる。
計算結果をグラフ表示してみると、ミクロの世界における自由電子の運動は、一定の速度での等速直線運動に量子力学的不確定性による量子ゆらぎが加わったジグザグ運動となることが分かる。

Excelに対して再計算の指示を出すと、乱数の値を変えながら再計算するので、そのたびに計算結果が変わり、各々の見本経路の様子がグラフに現れる。
マクロの世界では物体の質量が極めて大きいため、量子ゆらぎを0と考えて無視することができる。(1)式の量子ゆらぎの項を0にするように変更して計算すると、当然のことながら、古典力学における等速直線運動する質点の運動を示す直線が現れる。
ネルソンの確率力学の手法は、次のような利点をもつ。
まず第一に、古典力学と量子力学とは連続的につながった基本法則であり、両者が無関係に存在する法則ではないことを理解できる。
第二に、量子の位置とその運動量の不確定性を示す量子ゆらぎとはどういうものか目に見える形で表示できる。
第三の利点は、波動関数の重ね合わせに関するものである。自由電子は運動状態の重ね合わせが可能であるから、x軸方向に運動量pで自由運動する場合の波動関数1と同方向に-pで自由運動する場合の波動関数2の重ね合わせであるa×波動関数1+b×波動関数2を波動関数とする運動状態も存在する(a,bは各重みを示す)。
例えばa,b=1のように波動関数1と波動関数2を同じ重みで重ね合わせた波動関数の確率微分方程式をつくり、その計算結果をグラフで表示すると、量子力学的不確定性による小刻みな量子ゆらぎを示すが、ほぼ静止した運動となる。
ミクロの世界での重ね合わせの運動についての見本経路を拡大してグラフ表示してみる。何度か再計算するうちに、初期値であるx軸原点の近くで量子ゆらぎを示していたジグザグの運動経路が、途中の時点から瞬間的にx軸上の正点から負点のように反対符号の点に飛び移り、その後はしばらくその点の近くで量子ゆらぎを示すジグザグ運動を続けるような見本経路が現れる。
重ね合わせた波動関数に関するコペンハーゲン解釈は、電子が波動関数1の運動をしているか、あるいは波動関数2の運動をしているかを観測した場合、確率1/2で波動関数1の運動が観測され、確率1/2で波動関数2の運動が観測されるということしか教えない。この現象は、「波動関数の収縮」とよばれているが、そのメカニズムが明らかでない。
しかし、確率力学による電子の見本経路を見れば、それはただ電子の連続的な運動に伴う量子ゆらぎを意味しているのであって、観測によって波動関数が収縮するわけではないことが分かる。
一方、波動方程式を解いて波動関数を求めるかあるいは波動関数の数値解を計算する手法と比べて、一般に確率力学が不利となるケースが少なくないようにみえる。確率力学は、波動関数に依存しているので、波動関数が求まらなければ、(1)式のような確率微分方程式がつくれない。従って、波動関数が求まらず、その数値解を計算しなければならないケースには対応できないことが想定される。
Excelを使う確率微分方程式の計算では、量子ゆらぎの確率変数A(t)として、RAND()-0.5のような式を与えている。RAND()は0~1の範囲の一様乱数を生成する関数なので、この式は=-0.5~0.5の範囲の一様乱数を与える。
ゆらぎとは平均からのランダムなずれであるとするとき、ゆらぎは中心極限定理という確率法則に従い、ゆらぎの量は正規分布という確率分布によって与えられることが知られている。つまり、この確率分布こそ正規乱数とされる。
参考文献によれば、Excelが用意する乱数は一様乱数であるから、RAND()関数を12回足し合わせたものから6を引いた計算式によって確率変数A(t)を与えるのがよいとする。
実際に参考文献が勧める乱数の計算式によってA(t)を与えてみると、-0.5~0.5の範囲から外れる乱数が多く、計算結果の変動が激しくなり、不安定である。一様乱数を足し合わせるだけで正規乱数の準備ができるという話は疑問である。
古典力学から量子力学への遷移は連続的であることを基本法則とするのであれば、確率変数A(t)は正規乱数でなければならないことになる。特に、粒子の質量が量子のそれから次第に大きくなっていっても運動量保存則が常に成り立つものとすれば、粒子の質量が大きくなるに従って量子ゆらぎが小さくなるであろうから。
参考文献
保江邦夫著「Excelで学ぶ量子力学」(ブルーバックス)
蔵本由紀著「非線形科学」(集英社新書)









