2017年12月17日に人工知能の学習方法に関するブログを公開した後、いわゆる人工知能ではないが、ニューラルネットワークの様式を用いて組合せ最適化問題が解けることを確認しておこうと考えた。
巡回セールスマン問題とよばれるものは、組合せ最適化の代表的な例とされている。n個の都市を巡回しながら訪問するとき、多くの巡回経路がある中で、移動距離が最小となる(コストが最小となる)経路を最適解として見つける問題である。
一般にn個の都市を訪問する巡回路の数は(n-1)!個であり、都市間の移動距離が行きと帰りが同じであるから、距離の合計を計算しなければならない巡回路の総数は(n-1)!/2個になる。しかし、nが大きくなると、計算時間が爆発的に増加するので、現行の計算機では現実的な時間内では解けないことになる。
一方、この問題を解くために必要なアルゴリズムは、実行可能な巡回経路の組合せを列挙し、各組合せについて移動距離を集計し、移動距離が最小となる組合せを抽出するというきわめてシンプルなものである。
そこで、参考文献が紹介するnが小さい場合の例題について、Excelを用いて計算してみることにした。このとき、計算のための装備としてニューラルネットワーク的な構成手段が扱い易いことに気がついたのである。
例題は、チューリッヒ(Z)の自宅を出て、ベルリン(B)、ロンドン(L)、マドリッド(M)、ローマ(R)を可能な順序で巡回し、チューリッヒの自宅に戻るというものである。
この場合、n=5であるから、可能な巡回路の数は、4!=24であり、計算の必要があるケースの数はその半分の12である。
まず、Excelの表上に、都市間の移動距離を設定するためのテーブルを設け、データを入力する。
次に、可能な巡回路のケースを都市間の経路のシーケンスで表現することにする。一つのケースは、5つの経路のシーケンスとなる。各経路を上記テーブル上のセル番号で表す。このセル番号によって間接的に設定されたデータを参照できるように、=$D$2のように数式として記述する。このようにして、例えば、I,K,M,...,AE列のように12ケースの経路シーケンスを各々設定する。
この経路シーケンスは、ニューラルネットワークへの入力データであるから、各シーケンスに対応して中間層のユニットとなる一つのセル、例えばI8、を設ける。このセルに、対応するシーケンスの移動距離を合計する計算式を設定する。例えば、I列のシーケンスに対応して=I2+I3+I4+I5+I6を設定するなどである。
次に、I列の合計セルの数式をK,M,...,AE列の該当する同行セルに数式コピーする。
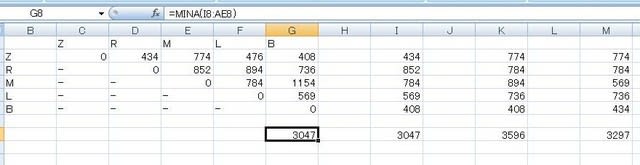
これによって、各経路シーケンスの合計移動距離が計算できるので、最後に、同行セルに空白以外の最小値を求める関数=MINA(I8:AE8)を設定すれば、移動距離の最小値が求められるから、対応する経路シーケンスが最適解となる。このセルが出力層のユニットに相当する。
参考文献
久保幹雄など著「インターネット時代の数学――離散数学と組合せ最適化」(共立出版)
巡回セールスマン問題とよばれるものは、組合せ最適化の代表的な例とされている。n個の都市を巡回しながら訪問するとき、多くの巡回経路がある中で、移動距離が最小となる(コストが最小となる)経路を最適解として見つける問題である。
一般にn個の都市を訪問する巡回路の数は(n-1)!個であり、都市間の移動距離が行きと帰りが同じであるから、距離の合計を計算しなければならない巡回路の総数は(n-1)!/2個になる。しかし、nが大きくなると、計算時間が爆発的に増加するので、現行の計算機では現実的な時間内では解けないことになる。
一方、この問題を解くために必要なアルゴリズムは、実行可能な巡回経路の組合せを列挙し、各組合せについて移動距離を集計し、移動距離が最小となる組合せを抽出するというきわめてシンプルなものである。
そこで、参考文献が紹介するnが小さい場合の例題について、Excelを用いて計算してみることにした。このとき、計算のための装備としてニューラルネットワーク的な構成手段が扱い易いことに気がついたのである。
例題は、チューリッヒ(Z)の自宅を出て、ベルリン(B)、ロンドン(L)、マドリッド(M)、ローマ(R)を可能な順序で巡回し、チューリッヒの自宅に戻るというものである。
この場合、n=5であるから、可能な巡回路の数は、4!=24であり、計算の必要があるケースの数はその半分の12である。
まず、Excelの表上に、都市間の移動距離を設定するためのテーブルを設け、データを入力する。
次に、可能な巡回路のケースを都市間の経路のシーケンスで表現することにする。一つのケースは、5つの経路のシーケンスとなる。各経路を上記テーブル上のセル番号で表す。このセル番号によって間接的に設定されたデータを参照できるように、=$D$2のように数式として記述する。このようにして、例えば、I,K,M,...,AE列のように12ケースの経路シーケンスを各々設定する。
この経路シーケンスは、ニューラルネットワークへの入力データであるから、各シーケンスに対応して中間層のユニットとなる一つのセル、例えばI8、を設ける。このセルに、対応するシーケンスの移動距離を合計する計算式を設定する。例えば、I列のシーケンスに対応して=I2+I3+I4+I5+I6を設定するなどである。
次に、I列の合計セルの数式をK,M,...,AE列の該当する同行セルに数式コピーする。
これによって、各経路シーケンスの合計移動距離が計算できるので、最後に、同行セルに空白以外の最小値を求める関数=MINA(I8:AE8)を設定すれば、移動距離の最小値が求められるから、対応する経路シーケンスが最適解となる。このセルが出力層のユニットに相当する。

参考文献
久保幹雄など著「インターネット時代の数学――離散数学と組合せ最適化」(共立出版)