「円周角の定理」を証明する

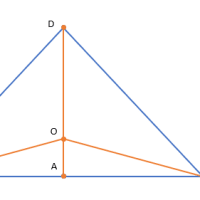
　NHKテレビの数学講座を見ていて、「円周角の定理」を知った。図に示すように、半径rの円周上に定点A,Bと動点Pがある。このとき、円周角APBは、一定値をとるというものである。



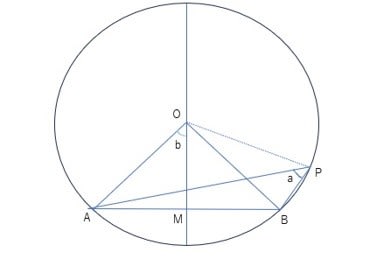
　円の中心をOとし、線分ABの中点をMとする。円周角APBの角度をaとする。角AOMの角度をbとする。三角形OABは二等辺三角形であるから、角OABと角OBAは等しく、各々の角度をcとする。つまり、2b+2c=PI(パイ)が成り立つ。角度2bをもつ角AOBを中心角という。

　角BOPの角度をdとする。三角形OAPは二等辺三角形であるから、角OAPと角OPAは等しく、各々の角度をeとする。三角形OAPについて内角の和をとると、
　　　d+2(b+e)=PI
となる。

　三角形OBPも二等辺三角形である。角OBPの角度をfとする。三角形OBPについて内角の和をとると、
　　　d+a+e+f=PI
となる。f=a+eであるから、
　　　d+2(a+e)=PI
となり、
　　　d+2(b+e)=d+2(a+e)
が成り立つ。
　すなわち、a=bとなり、円周角APBは中心角AOBの半分に等しいことが証明された。