算額(その1304)
百十五 群馬県富岡市一宮 貫前神社 明治4年(1871)
群馬県和算研究会:群馬の算額,上武印刷株式会社,高崎市,1987年3月31日.
キーワード:円1個,正三角形,正五角形
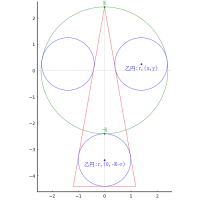
正三角形の中に円,長方形,五角形を容れる。円の直径が 10 寸のとき,正五角形の一辺の長さはいかほどか。

1. 円の半径を r とおく。IE = r
2. 円を内包する正三角形の一辺の長さを 2a とおく。EF = a = √3r
3. 正五角形を内包する円の半径を R とおく。AE = AB = AD = R
4. EF = AB*cosd(18°) = R*cosd(18°) = a = √3r
5. R*cosd(18°) = √3r より,R = √3r/cosd(18°)
6. 正五角形の一辺の長さ = 2CD = 2*R*sind(36°)
7. 2*R*sind(36°) = 2 * (√3r/cosd(18°)) * sind(36°)
8 r = 10/2 のとき s = 2 * (√3(10/2)/cosd(18)) * sind(36) = 10.704662693192699
9. 図を描くために必要な正三角形の一辺の長さを 2b とすると,相似関係から CH = b = a + (yo + R)/√3
以上により,円の直径が 10 寸のとき,正五角形の一辺の長さは 10.704662693192699 寸である。
2 * (√3(10/2)/cosd(18)) * sind(36)
10.704662693192699
s は三角関数を含むが,cosd(18), sind(36) はルートを含む式で表せるので,以下のように簡略化される。
s = 5(√15 - √3) = 10.704662693192699
include("julia-source.txt");
using SymPy
@syms d, r
s = 2r * (√Sym(3)/cosd(Sym(18))) * sind(Sym(36)) |> simplify
s/r |> x -> apart(x, d) |> simplify |> x -> x*r |> println
r*(-sqrt(3) + sqrt(15))
円の直径が 10 寸のとき,正五角形の一辺の長さは 5(√15 - √3) = 10.704662693192699。
function draw(r, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
a = √3r
R = a/cosd(18)
xo = R*sind(36)
yo = R*cosd(36)
plot()
circle(0, yo + R + r, r, :blue)
plot!([a, 0, -a, a], (yo + R) .+ [0, √3a, 0, 0], color=:green, lw=0.5)
θ = 18:72:378
x = R.*cosd.(θ)
y = R.*sind.(θ)
circle(0, yo, R, :pink)
plot!(x, yo .+ y, color=:red, lw=0.5)
plot!([a, a, -a, -a, a], [0, yo + R, yo + R, 0, 0], color=:orange, lw=0.5)
b = a + (yo + R)/√3
plot!([b, 0, -b, b], [0, yo + R + √3a, 0, 0], color=:black, lw=0.5)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, yo, " A", :green, :left, :vcenter)
point(x[1], yo + y[1], " B", :green, :left, :vcenter)
point(0, 0, "C", :green, :center, delta=-delta)
point(R*sind(36), 0, "D", :green, :center, delta=-delta)
point(0, yo + R, "E", :green, :center, delta=-delta)
point(R*cosd(18), yo + R, " F", :green, :left, :vcenter)
point(a, 0, "G", :green, :left, delta=-delta)
point(b, 0, "H", :green, :left, delta=-delta)
point(0, yo + R + r, " I", :green, :left, :vcenter)
point(0, yo + R + √3a, " J", :green, :left, :vcenter)
point(0, yo + R + r, "")
end
end;
draw(10/2, true)