x = range(0, 5, length=6)
y = @. exp(-x)
#=
6-element Vector{Float64}:
1.0
0.36787944117144233
0.1353352832366127
0.049787068367863944
0.01831563888873418
0.006737946999085467
=#
というデータがある。y を x の多項式 a0 + a1*x + a2*x^2 + ... で予測すること(多項式回帰)を考える。
多項式回帰は x^2, x^3, ... を前もって用意しておけば重回帰プログラムを使えばできる。
理論上は x の次数は length(y) - 1 までなので,例の場合は 5 次の項まで使える。
using DataFrames
df = DataFrame(:x => x, :x2 => x.^2, :x3 => x.^3, :x4 => x.^4, :x5 => x.^5, :y => y)
#=
6 rows × 6 columns
x x2 x3 x4 x5 y
Float64 Float64 Float64 Float64 Float64 Float64
1 0.0 0.0 0.0 0.0 0.0 1.0
2 1.0 1.0 1.0 1.0 1.0 0.367879
3 2.0 4.0 8.0 16.0 32.0 0.135335
4 3.0 9.0 27.0 81.0 243.0 0.0497871
5 4.0 16.0 64.0 256.0 1024.0 0.0183156
6 5.0 25.0 125.0 625.0 3125.0 0.00673795
=#
重回帰プログラムは GLM にある lm() を使う。
using GLM
lmans2 = lm(@formula(y ~ x + x2), df); # 2 次式
coef(lmans2)
#= 0, 1, 2 次の係数(以下同様)
3-element Vector{Float64}:
0.9313226293358078
-0.5231411796668056
0.0697679508663814
=#
lmans3 = lm(@formula(y ~ x + x2 + x3), df); # 3 次式
coef(lmans3)
#=
4-element Vector{Float64}:
0.9917995957122201
-0.7993193261190775
0.22096036680740455
-0.0201589887921363
=#
lmans4 = lm(@formula(y ~ x + x2 + x3 + x4), df); # 4 次式
coef(lmans4)
#=
5-element Vector{Float64}:
0.9995995032132226
-0.9293177844691326
0.36070870953370876
-0.0656584492146525
0.0045499460422515035
=#
lmans5 = lm(@formula(y ~ x + x2 + x3 + x4 + x5), df); # 5 次式
coef(lmans5)
#=
6-element Vector{Float64}:
0.9999999999998723
-0.9762026083014735
0.4413086878624456
-0.11144858183069759
0.015062986693944548
-0.0008410432521384522
=#
5次多項式による予測値
predict(lmans5)
#=
6-element Vector{Float64}:
0.9999999999998723
0.36787944117195287
0.13533528323580923
0.04978706836849145
0.018315638888491637
0.006737946999125999
=#
多項式回帰を行う fit() が Polynomials にある。
次数が高い項を使うと,正規方程式は不安定になるが,Polynomials.fit() だと,不安定性を軽減する計算アルゴリズムが採用される。
using Plots, Polynomials
注:以下では Polynomials.fit() として使っているが,これは先に使った GLM の fit() と識別するためなので,通常は fit() だけでよい。
f2 = Polynomials.fit(x, y, 2); # 2次式で予測
# 0.9313226293358072 - 0.5231411796668045∙x + 0.06976795086638117∙x2
f3 = Polynomials.fit(x, y, 3); # 3次式で予測
# 0.9917995957122127 - 0.7993193261190567∙x + 0.22096036680739517∙x2 - 0.02015898879213521∙x3
f4 = Polynomials.fit(x, y, 4); # 4次式で予測
# 0.9995995032131947 - 0.9293177844687606∙x + 0.360708709533328∙x2 - 0.06565844921453219∙x3 + 0.004549946042239714∙x4
f5 = Polynomials.fit(x, y); # 最高次数 = length(x) - 1 = 5次式で予測
# 1.0 - 0.9762026083107394∙x + 0.4413086878778398∙x2 - 0.11144858183923873∙x3 + 0.015062986695871163∙x4 - 0.0008410432522905108∙x5
データにある x の範囲内だと次数が高いほど予測が上手くできるように見えるが,

scatter(x, y, grid=false, tick_direction=:out,
markerstrokewidth=0, size=(400, 300),
xlabel="\$x\$", ylabel="\$y\$", label="Data")
plot!(f2, extrema(x)..., label="Order2")
plot!(f3, extrema(x)..., label="Order3")
plot!(f4, extrema(x)..., label="Order4")
plot!(f5, extrema(x)..., label="Order5")
savefig("fig1.png")
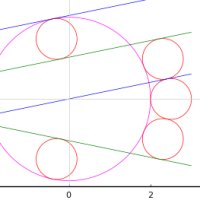
範囲外では全くダメなのがよく分かる。

scatter(x, y, grid=false, tick_direction=:out,
markerstrokewidth=0, size=(400, 300),
xlims=(-3,8),
xlabel="\$x\$", ylabel="\$y\$", label="Data")
plot!(f2, [-3,8]..., label="Order2")
plot!(f3, [-3,8]..., label="Order3")
plot!(f4, [-3,8]..., label="Order4")
plot!(f5, [-3,8]..., label="Order5")
savefig("fig2.png")
また,単調減少や単調増加の場合は目立たないが,そうでない場合にはデータ範囲内でもデータ点は通っても,それ以外の所は凸凹で,予測とはとてもいえないことが明らかである。
x2 = 0:5
y2 = [2,6,9,4,11,7]
f52 = Polynomials.fit(x2, y2); # degree = length(x) - 1 = 5
scatter(x2, y2, grid=false, tick_direction=:out,
markerstrokewidth=0, size=(400, 300),
xlabel="\$x\$", ylabel="\$y\$", label="")
plot!(f52, [-0.3,5.3]..., label="")
savefig("fig3.png")