（1236）「象は鼻が長い」の「象は｛∀ｘ（象ｘ→｝」について。

（01）
学校文法は単純な英語文法からの輸入で、主語・述語関係を単純に当てはめたものだ。そのため、「象は、鼻が長い」という単純な文でさえ、どれが主語だか指摘できず、複数主語だとか、主語の入れ子だとか、奇矯な技を使う。これに対して三上は、日本語には主語はない、とする。「象は」は、テーマを提示する主題であり、これから象についてのことを述べますよ」
従って、
（01）（02）により、
（03）
① 象は動物である。⇔
① ∀ｘ（象ｘ→動物ｘ）⇔
① すべてのｘについて（ｘが象であるならば、ｘは動物である）。
然るに、
（04）
１　　　　　（１）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝　Ａ
　２　　　　（２）∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆∀ｚ（耳ｚｘ→～鼻ｚｘ）｝　Ａ
　　３　　　（３）∃ｘ（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　Ａ
１　　　　　（４）　　　象ａ→∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　１ＵＥ
　２　　　　（５）　　　兎ａ→∃ｙ（長ｙ＆耳ｙａ）＆∀ｚ（耳ｚａ→～鼻ｚａ）　　２ＵＥ
　　　６　　（６）　　　兎ａ＆象ａ　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　６　　（７）　　　兎ａ　　　　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
　　　６　　（８）　　　　　　象ａ　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
１　　６　　（９）　　　　　　∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　４８ＭＰＰ
　２　６　　（ア）　　　　　　∃ｙ（長ｙ＆耳ｙａ）＆∀ｚ（耳ｚａ→～鼻ｚａ）　　５７ＭＰＰ
１　　６　　（イ）　　　　　　∃ｙ（鼻ｙａ＆長ｙ）　　　　　　　　　　　　　　　９＆Ｅ
　　　　ウ　（ウ）　　　　　　　　　鼻ｂａ＆長ｂ　　　　　　　　　　　　　　　　Ａ
　２　６　　（エ）　　　　　　∃ｙ（長ｙ＆耳ｙａ）　　　　　　　　　　　　　　　ア＆Ｅ
　　　　　オ（オ）　　　　　　　　　長ｂ＆耳ｂａ　　　　　　　　　　　　　　　　Ａ
　　　　　オ（カ）　　　　　　　　　　　　耳ｂａ　　　　　　　　　　　　　　　　オ＆Ｅ
１　　６　　（キ）　　　　　　　　　　　　　　　　　∀ｚ（～鼻ｚａ→～長ｚ）　　９＆Ｅ
　２　６　　（ク）　　　　　　　　　　　　　　　　　∀ｚ（耳ｚａ→～鼻ｚａ）　　ア＆Ｅ
１　　６　　（ケ）　　　　　　　　　　　　　　　　　　　　～鼻ｂａ→～長ｂ　　　キＵＥ
　２　６　　（コ）　　　　　　　　　　　　　　　　　　　　耳ｂａ→～鼻ｂａ　　　クＵＥ
　２　６　オ（サ）　　　　　　　　　　　　　　　　　　　　　　　　～鼻ｂａ　　　カコＭＰＰ
１２　６　オ（シ）　　　　　　　　　　　　　　　　　　　　　　　　　～長ｂ　　　ケサＭＰＰ
　　　　　オ（ス）　　　　　　　　　長ｂ　　　　　　　　　　　　　　　　　　　　オ＆Ｅ
１２　６　オ（セ）　　　　　　　　　長ｂ＆～長ｂ　　　　　　　　　　　　　　　　シス＆Ｉ
１２　６　　（ソ）　　　　　　　　　長ｂ＆～長ｂ　　　　　　　　　　　　　　　　エオセＥＥ
１２３　　　（タ）　　　　　　　　　長ｂ＆～長ｂ　　　　　　　　　　　　　　　　３６ソＥＥ
１２　　　　（チ）～∃ｘ（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　３タＲＡＡ
１２　　　　（ツ）∀ｘ～（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　チ量化子の関係
１２　　　　（テ）　　～（兎ａ＆象ａ）　　　　　　　　　　　　　　　　　　　　　ツＵＥ
１２　　　　（ト）　　～兎ａ∨～象ａ　　　　　　　　　　　　　　　　　　　　　　テ、ド・モルガンの法則
１２　　　　（ナ）　　　兎ａ→～象ａ　　　　　　　　　　　　　　　　　　　　　　ト含意の定義
１２　　　　（ニ）∀ｘ（兎ｘ→～象ｘ）　　　　　　　　　　　　　　　　　　　　　ナＵＩ
従って、
（04）により、
（05）
（ⅰ）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。然るに、
（ⅱ）∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆∀ｚ（耳ｚｘ→～鼻ｚｘ）｝。従って、
（ⅲ）∀ｘ（兎ｘ→～象ｘ）。
といふ「推論（三段論法）」、すなはち、
（ⅰ）すべてのｘについて｛ｘが象であるならば、あるｙはｘの鼻であって、長く、すべてのｚについて（ｚがｘの鼻でないならば、ｚは長くない）｝。　　　然るに、
（ⅱ）すべてのｘについて｛ｘが兎であるならば、あるｙは長くて、ｘの耳であり、すべてのｚについて（ｚがｘの耳であるならば、ｚはｘの鼻ではない）｝。従って、
（ⅲ）すべてのｘについて（ｘが兎であるならば、ｘは象ではない。）
といふ「推論（三段論法）」は、「妥当」である。
従って、
（05）により、
（06）
（ⅰ）象は鼻が長い。然るに、
（ⅱ）兎の耳は長いが、耳は鼻ではない。従って、
（ⅲ）兎は象ではない。
といふ「推論（三段論法）」は、「妥当」である。
従って、
（04）（05）（06）により、
（07）
② 象は鼻が長い。
といふ「日本語」は、
② ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。
といふ「述語論理式」に「相当」する。
従って、
（03）（07）により、
（08）
① 象は動物である。
② 象は鼻が長い。
といふ「日本語」は、
① ∀ｘ（象ｘ→動物ｘ）
② ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。
といふ「述語論理式」に「相当」する。
然るに、
（09）
「象ｘ（ｘは象である。）」
のやうな「それ」を「ｘの命題関数（propositional function）」と言ふ。
然るに、
（10）
① ∀ｘ（象ｘ→Ｐ）
に於いて、
① Ｐは「ｘの命題関数」であるとする。
然るに、
（11）
① ∀ｘ（象ｘ→Ｐ）
に於いて、
① Ｐ＝動物ｘ
② Ｐ＝∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）
といふ「代入（置き換へ）」を行ふと、
① ∀ｘ（象ｘ→動物ｘ）
② ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝
従って、
（11）により、
（12）
① ∀ｘ（象ｘ→動物ｘ）
② ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝
といふ「述語論理式」は、両方とも、
① ∀ｘ（象ｘ→Ｐ）
② ∀ｘ（象ｘ→Ｐ）
といふ『文型』をしてゐる。
従って、
（08）（12）により、
（13）
「述語論理式」を「基準」にするならば、
① 象は動物である。
② 象は鼻が長い。
といふ「日本語」は、両方とも、
① ∀ｘ（象ｘ→Ｐ）
② ∀ｘ（象ｘ→Ｐ）
といふ『文型』をしてゐる。
従って、
（13）により、
（14）
「述語論理式」を「基準」にするならば、
① 象は動物である。
② 象は鼻が長い。
に於ける、
① 象は・・・・・。
② 象は・・・・・。
といふ「日本語」は、両方とも、
① ∀ｘ（象ｘ→　）
② ∀ｘ（象ｘ→　）
といふ『型』をしてゐる。
従って、
（14）により、
（15）
① 象は動物である。
② 象は鼻が長い。
といふ「日本語」に於ける、
① 象は
② 象は
は、『述語論理の文法（文型）』を「基準」にすると、「区別」をする「必要」が無い。
従って、
（15）により、
（16）
① 象は動物である。
② 象は鼻が長い。
に於いて、
①「象は」が「主語」であるならば、
②「象は」も「主語」である。

（1235）「太陽系は地球が第三惑星である（二重主語文）」と「述語論理」。

（01）
１　　（１）∀ｘ（惑星ｘ→～太陽ｘ）　Ａ
　２　（２）∃ｘ（地球ｘ＆　惑星ｘ）　Ａ
１　　（３）　　　惑星ａ→～太陽ａ　　１ＵＥ
　　４（４）　　　地球ａ＆　惑星ａ　　Ａ
　　４（５）　　　地球ａ　　　　　　　４＆Ｅ
　　４（６）　　　　　　　　惑星ａ　　４＆Ｅ
１　４（７）　　　　　　　～太陽ａ　　３６ＭＰＰ
１　４（８）　　　地球ａ＆～太陽ａ　　５７＆Ｉ
１　４（９）∃ｘ（地球ｘ＆～太陽ｘ）　８ＥＩ
１２　（ア）∃ｘ（地球ｘ＆～太陽ｘ）　２４９ＥＥ
従って、
（01）により、
（02）
（ⅰ）∀ｘ（惑星ｘ→～太陽ｘ）
（ⅱ）∃ｘ（地球ｘ＆　惑星ｘ）
（ⅲ）∃ｘ（地球ｘ＆～太陽ｘ）
といふ「推論（三段論法）」、すなはち、
（ⅰ）すべてのｘについて（ｘが惑星であるならば、ｘは太陽ではない）。
（ⅱ）あるｘは（地球であって、惑星である）。
（ⅲ）あるｘは（地球であって、太陽ではない）。
といふ「推論（三段論法）」は、「妥当」である。
従って、
（02）により、
（03）
（ⅰ）惑星は太陽ではない。然るに、
（ⅱ）地球は惑星である。　従って、
（ⅲ）地球は太陽ではない。
といふ「推論（三段論法）」は、「妥当」である。
然るに、
（04）
１　　　　　（１）∀ｘ｛太陽系ｘ→∃ｙ［（地球ｙ＆第三惑星ｙｘ）＆∀ｚ（第三惑星ｚｘ→ｙ＝ｚ）］｝　Ａ
１　　　　　（２）　　　太陽系ａ→∃ｙ［（地球ｙ＆第三惑星ｙａ）＆∀ｚ（第三惑星ｚａ→ｙ＝ｚ）］　　１ＵＥ
　３　　　　（３）　　　太陽系ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Ａ
１３　　　　（４）　　　　　　　　∃ｙ［（地球ｙ＆第三惑星ｙａ）＆∀ｚ（第三惑星ｚａ→ｙ＝ｚ）］　　２３ＭＰＰ
　　５　　　（５）　　　　　　　　　　　（地球ｂ＆第三惑星ｂａ）＆∀ｚ（第三惑星ｚａ→ｂ＝ｚ）　　　Ａ
　　５　　　（６）　　　　　　　　　　　（地球ｂ＆第三惑星ｂａ）　　　　　　　　　　　　　　　　　　５＆Ｅ
　　５　　　（７）　　　　　　　　　　　　　　　　　　　　　　　　∀ｚ（第三惑星ｚａ→ｂ＝ｚ）　　　５＆Ｅ
　　５　　　（８）　　　　　　　　　　　　　　　　　　　　　　　　　　　第三惑星ｃａ→ｂ＝ｃ　　　　７ＵＥ
　　　９　　（９）　　　　∃ｚ（火星ｚ＆～地球ｚ）　　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　　ア　（ア）　　　　　　　火星ｃ＆～地球ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　　ア　（イ）　　　　　　　火星ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　ア＆Ｅ
　　　　ア　（ウ）　　　　　　　　　　　～地球ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　ア＆Ｅ
　　　　　エ（エ）　　　　　　　　　　　　ｂ＝ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　　アエ（オ）　　　　　　　　　　　～地球ｂ　　　　　　　　　　　　　　　　　　　　　　　　　　ウエ＝Ｅ
　　５　　　（カ）　　　　　　　　　　　　地球ｂ　　　　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
　　５　アエ（キ）　　　　　　　　　　　～地球ｂ＆地球ｂ　　　　　　　　　　　　　　　　　　　　　　オカ＆Ｉ
　　５　ア　（ク）　　　　　　　　　　　　ｂ≠ｃ　　　　　　　　　　　　　　　　　　　　　　　　　　エキＲＡＡ
　　５　ア　（ケ）　　　　　　　　　　　　　　　　　　　　　　　 　　～第三惑星ｃａ　　　　　　　　 ８クＭＴＴ
　　５　ア　（コ）　　　　　　　火星ｃ＆～第三惑星ｃａ　　　　　　　　　　　　　　　　　　　　　　　イケ＆Ｉ
　　５　ア　（サ）　　　　∃ｚ（火星ｚ＆～第三惑星ｚａ）　　　　　　　　　　　　　　　　　　　　　　コＥＩ
　　５９　　（シ）　　　　∃ｚ（火星ｚ＆～第三惑星ｚａ）　　　　　　　　　　　　　　　　　　　　　　９アサＥＥ
１３　９　　（ス）　　　　∃ｚ（火星ｚ＆～第三惑星ｚａ）　　　　　　　　　　　　　　　　　　　　　　４５シＥＥ
１　　９　　（セ）　　　太陽系ａ→∃ｚ（火星ｚ＆～第三惑星ｚａ）　　　　　　　　　　　　　　　　　　３スＣＰ
１　　９　　（ソ）∀ｘ｛太陽系ｘ→∃ｚ（火星ｚ＆～第三惑星ｚｘ）｝　　　　　　　　　　　　　　　　　セＵＩ
従って、
（04）により、
（05）
（ⅰ）∀ｘ｛太陽系ｘ→∃ｙ［（地球ｙ＆第三惑星ｙｘ）＆∀ｚ（第三惑星ｚｘ→ｙ＝ｚ）］｝
（ⅱ）∃ｚ（火星ｚ＆～地球ｚ）
（ⅲ）∀ｘ｛太陽系ｘ→∃ｚ（火星ｚ＆～第三惑星ｚｘ）｝
といふ「推論（三段論法）」、すなはち、
（ⅰ）すべてのｘについて｛ｘが太陽系であるならば、あるｙは［（地球であってｘの第三惑星）であって、すべてのｚについて（ｚがｘの第三惑星であるならば、ｙとｚは「同一」である）］｝。
（ⅱ）あるｚは（火星であって、ｚは地球ではない。）
（ⅲ）すべてのｘについて｛ｘが太陽系であるならば、あるｚは（火星であって、ｚはｘの第三惑星ではない）｝。
といふ「推論（三段論法）」は、「妥当」である。
従って、
（05）により、
（06）
（ⅰ）太陽系は地球が第三惑星であって、地球以外は第三惑星ではない。然るに、
（ⅱ）火星は、地球ではない。従って、
（ⅲ）太陽系の第三惑星は、火星ではない。
といふ「推論（三段論法）」は、「妥当」である。
然るに、
（07）
（ⅰ）太陽系は地球が第三惑星である。然るに、
（ⅱ）火星は、地球ではない。　　　　従って、
（ⅲ）太陽系の第三惑星は、火星ではない。
といふ「推論（三段論法）」は、「妥当」である。
従って、
（01）～（07）により、
（08）
① 　惑星は
② 太陽系は
といふ「日本語」は、両方とも、「述語論理」といふ「観点」からすれば、
① すべてのｘについて（ｘが　惑星ならば、
② すべてのｘについて（ｘが太陽系ならば、
といふ「意味」である。
従って、
（08）により、
（09）
「述語論理」を「基準」にすれば、
① 　惑星は太陽ではない。
② 太陽系は地球が第三惑星である。
に於ける、
① 　惑星は
② 太陽系は
に於いて、
① は「主語」であって、
② も「主語」である。
然るに、
（10）
① 　惑星は、太陽ではない。
② 太陽系は、地球が第三惑星である。
③ 太陽系の第三惑星は、地球である。
に対する「英訳」は、
① A planet is not the sun.
② In the solar system, the earth is the third planet.
③ The third planet of the solar system is the earth.
である。
然るに、
（11）
② In the solar system,
は「副詞（句）」であって、「主語」ではない。
従って、
（10）（11）により、
（12）
「英語」を「基準」にすれば、
① 　惑星は（太陽ではない）。
② 太陽系は（地球が第三惑星である）。
に於ける、
① 　惑星は
② 太陽系は
に於いて、
① は「主語」であって、
② は「副詞」である。
従って、
（09）（12）により、
（13）
① 太陽系は（地球が第三惑星である）。
② 太陽系は（地球が第三惑星である）。
に於いて、
①「太陽系は」は、「述語論理」からすれば、「主語」であって、
②「太陽系は」は、「英語文法」からするば、「副詞」である。
従って、
（14）
① 象は（鼻が長い）。
①「象は」は、「述語論理」からすれば、「主語」であって、
②「象は」は、「英語文法」からするば、「副詞」である。
然るに、
（15）
「象は鼻が長い」という文が大正年間から専門家を悩ませていた。「象は」も主語、「鼻が」も主語。ひとつのセンテンスに二つも主語があってはならない。しかし、この表現は誤りではない。どう説明、合理化したらよいか、というのである。うまく解決する方法は見つからなかった。戦後になって三上章という人がおもしろい説を出した。「象は」は主語ではなくて主題である。「鼻が長い」は主語と述語だというので、これなら二重主語でなくなる。主題というのは、〝 についていえば〝 のように範囲を示す、いわば副詞のようなものだと考える。副詞なら主語になれない（外山滋比古）。
従って、
（14）（15）により、
（16）
「象は」は「主語」、「鼻が」も「主語」であっても良いし、
「象は」は「副詞」、「鼻が」は「主語」であっても、どちらでも良い。

（1234）「ある誤診」について（白い巨塔との比較）。

（01）
①「肺の陰影」は「炎症性変化」である（財前教授）。
②「肺の陰影」は「癌の転移」である（里見助教授）。
③「肺の陰影」は「癌の転移」である（病理解剖の結果）。
然るに、
（02）
③「病理解剖の結果」は「正しい」。
従って、
（01）（02）により、
（03）
①「肺の陰影」は「炎症性変化」である（財前教授）。
②「肺の陰影」は「癌の転移」である（里見助教授）。
に於いて、
① は『誤診』であって、
② は『誤診』ではない。
然るに、
（04）
④ 唐木教授（鑑定人）曰く、
　現実には、佐々木庸平氏は、術後、癌性リンパ管症の急速な進行により死に至りましたが、
　臨床症状、レントゲン所見、検査所見等から、肺炎を第一に疑うことは、当然である。
　しかし、術後肺炎の治療として、投与された抗生物質が、１月８日、午後４時頃の段階で、
　奏効しなくなったわけですから、その時点で診断の見直しをしなかったという点については、
　疑問の余地を残すところであります。
然るに、
（05）
⑤ 裁判官曰く、
　主文。
　一、原告ら請求を棄却する。
　二、訴訟費用は、原告ら負担とする。
　財前教授が、炎症性変化と診断し、手術を行ったことは、間違いとは言えない。
　死因の癌性リンパ管症は、本件の場合、あくまで、死後、解剖を行うことで、
　初めて、診断が可能なことであり、その『結果論』で、医師の責任を問うのは、
　医師に対し、あまりに、過酷な要求と言える。
従って、
（03）（04）（05）により、
（06）
財前教授の「診断」は『誤診』ではあったが、
財前教授が「不注意」であったとは言えないが故に、
財前教授は「無罪」である。
従って、
（06）により、
（07）
①『誤診』自体による「有罪」は無く、
②「不注意」による『誤診』であれば「有罪」である。
然るに、
（08）
１　　　（１）　Ｐ→（Ｑ→　Ｒ）　Ａ
　２　　（２）　　　　Ｑ＆～Ｒ　　Ａ
　　３　（３）　　　　Ｑ→　Ｒ　　Ａ
　２　　（４）　　　　Ｑ　　　　　２＆Ｅ
　２３　（５）　　　　　　　Ｒ　　３４ＭＰＰ
　２　　（６）　　　　　　～Ｒ　　２＆Ｅ
　２３　（７）　　　　Ｒ＆～Ｒ　　５６＆Ｉ
　２　　（８）　　～（Ｑ→　Ｒ）　３７ＲＡＡ
１２　　（９）～Ｐ　　　　　　　　１８ＭＴＴ
１　　　（ア）（Ｑ＆～Ｒ）→～Ｐ　２９ＣＰ
　　　イ（イ）　　　　　　　　Ｐ　Ａ
　　　イ（ウ）　　　　　　～～Ｐ　イＤＮ
１　　イ（エ）　～（Ｑ＆～Ｒ）　　アウＭＴＴ
１　　イ（オ）　　～Ｑ∨　Ｒ　　　エ、ド・モルガンの法則
１　　イ（カ）　　　Ｑ→　Ｒ　　　オ含意の定義
１　　　（キ）Ｐ→（Ｑ→　Ｒ）　　イカＣＰ
従って、
（08）により、
（09）
①　Ｐ→（Ｑ→Ｒ）
②（Ｑ＆～Ｒ）→～Ｐ
に於いて、
①＝② は、「（逆ではなく）対偶である」。
従って、
（09）により、
（10）
Ｐ＝術後肺炎である。
Ｑ＝抗生物質を投与する。
Ｒ＝熱が下がる。
であるとして、
① 術後肺炎であるならば（抗生物質を投与すれば、熱が下がる）。
②（抗生物質を投与しても、熱が下がらない）ならば術後肺炎ではない。
に於いて、
①＝② は、「（逆ではなく）対偶である」。
従って、
（10）により、
（11）
① 脱水であるならば（点滴をすれば、数値が下がる）。
②（点滴をしても、数値が下がらない）ならば脱水ではない。
に於いて、
①＝② も、「（逆ではなく）対偶である」。
然るに、
（12）

従って、
（11）（12）により、
（13）
Ｓ医師は、
① 脱水であるため（点滴をすれば、数値は下がる）。⇔
②（点滴をしても、数値が下がらない）ならば脱水ではない。
という風に、「診断」をしている。
然るに、
（14）

従って、
（14）により、
（15）

「クレアチニン」に関しては、「むしろ、上昇している」し、
「尿素窒素（ＢＵＮ）」は、「下がった」とは言え、「３倍が、２.５倍になっている」に過ぎない。
従って、
（13）（14）（15）により、
（16）
②（点滴をしても、数値が下がらない）ならば脱水ではない。然るに、
②（点滴をしても、数値が下がらない）。従って、
② 脱水ではない。
従って、
（13）（16）により、
（17）
① 脱水であるため（点滴をすれば、数値は下がる）。⇔
②（点滴をしても、数値が下がらない）ならば脱水ではない。
という風に、「診断」をしているが、
② 脱水ではない。
然るに、
（18）

従って、
（04）（10）（11）（17）（18）により、
（19）
財前先生は、「癌性リンパ管症」を、「術後肺炎」であると『誤診』し、
　Ｓ先生は、「急性腎不全」を、　　「脱水」　　であると『誤診』している。
然るに、
（20）

従って、
（20）により、
（21）
「患者の持病」は、「痛風（高尿酸血症）」と「慢性腎臓病」と「悪性貧血」の、「３つ」であった。
従って、
（21）により、
（22）
Ｓ医師は、「患者」の「クレアチニン・赤血球・尿酸値」に対しては、「特に、注意」を払っていたことになり、そうでなければ、医師として「怠慢」であると、言わざるを得ない。
然るに、
（23）

従って、
（23）により、
（24）
Ｓ医師は、「点滴をすると、　血液が希釈され、　赤血球の値が、低下すること」　を知っていた。⇔
Ｓ医師は、「点滴をしないと、血液は希釈されず、赤血球の値が、低下しないこと」を知っていた。
然るに、
（25）

従って、
（14）（25）により、
（26）
実を言うと、「２０１９年０１月２５日の赤血球の値（２.４６）」は、「中央値（メディアン）」であって、それ故、
「２０１９年０１月２５日」に於いて、「患者」は、「脱水（血液濃縮）」を、起こしてはいない。
従って、
（19）（22）（26）
（27）
（ⅰ）Ｓ先生は、「急性腎不全」を、「脱水」であると『誤診』している。
（ⅱ）Ｓ医師は、「患者」の「クレアチニン・赤血球・尿酸値」に対しては、「特に、注意」を払っていたことになり、そうでなければ、医師として「怠慢」である。
（ⅲ）「２０１９年０１月２５日」に於いて、「患者」は、「脱水（血液濃縮）」を、起こしてはいない。
従って、
（07）（27）により、
（28）
①『誤診』自体による「有罪」は無く、
②「不注意」による『誤診』であれば「有罪」であるが、
Ｓ先生は、『不注意による誤診』であるし、尚且つ、「患者」は、『誤診の４日後』に、「死亡」している。
然るに、
（29）
関口弁護士：
癌治療において、医者と患者が向き合うために、不可欠なものは、何でしょう。
里見先生：
それは、話すということに、尽きると思います。
財前は、選択の可能性があることを、説明せず、オペ以外の選択は無いと、言い切った。
然るに、
（30）
裁判官：
主文。
一、現判決を、次の通リ変更する。・・・・・。
尚、判決の社会的影響を考え、次に、判決理由の要旨を述べます。
被控訴人、財前の治療行為そのものは、十分に、平均的水準を上回るもので、法的に、責められるものではない。
しかし、あらゆる治療行為が、リスクを伴ったものである以上、患者への、真摯の説明と、それに基づく、「同意」が、「必要不可欠」となる。
にも拘わらず、被控訴人財前は、「手術以外の方法」を、「助かりたいなら、手術しか無い」の一言で、退けた事実があり、その「過失」は、否定しがたい。
従って、
（29）（30）により、
（31）
財前五郎は、「インフォームドコンセント」を怠った（患者と、話し合わなかった）が故に、「有罪」となっている。
従って、
（06）（30）（31）により、
（32）
「一審」に於いて、
財前教授の「診断」は『誤診』ではあったが、
財前教授が「不注意」であったとは言えないが故に、
財前教授は「無罪」であるとされたものの、
「二審」に於いて、
財前五郎は、「インフォームドコンセント」を怠った（患者と、話し合わなかった）が故に、「有罪」となっている。
然るに、
（33）

然るに、
（33）により、
（34）
「薬剤の投与」が無くとも、「尿酸値」が「正常」になったにも拘わらず、

というような「危険な薬剤（禁忌）の投与」の「承諾」を、私であろうと、私以外の誰であろうと、するはずがありませんし、「投与の承諾」はしていない、ということに関しては、「電子カルテ」以外の「記録」によって、「完璧に証明」出来ます。
然るに、
（35）
2 刑事責任
医療過誤は場合によっては業務上過失致死傷罪（刑法211条）に該当することがありますが、民事損害賠償責任とは異なり、国家刑罰権の発動ですので、患者が死亡しかつ過誤が初歩的ミスの場合のような重大な不注意で患者が死亡した場合に限って起訴されることが多いのが実情です（学陽書房、医療事故の法律相談〈全訂版〉、2009年、12頁）。
従って、
（28）（32）～（35）により、
（36）
少なくとも、私自身は、Ｓ医師（社会医療法人、副院長）が、「刑事事件の被告」として、「有罪」であることを、確信している。

（1233）これから「弁護士を介して病院に送付する質問書」の一部です。

従って、

（15）（19）により、

（20）

という、「赤血球とヘモグロビンとヘマトリック」とは異なり、

という、「赤血球とクレアチニン（Ｃｒｅ）」は、

「２つの値が、並行して変化する」ということが、全く無い。

従って、

（12）（20）により、

（21）

「患者ID0000123456」の場合も、確かに、

「赤血球とヘモグロビンとヘマトリック」に関しては、「３つの値が並行して変化する」が、その一方で、

「赤血球とクレアチニン」に関しては、「２つの値が並行して変化する」ということが、全く無い。

然るに、

（05）～（10）により、

（22）

もう一度、「確認」すると、

（１）脱水によって腎機能が悪化しているのであれば、 　　　赤血球とクレアチニンは並行して変化しなければならない。 （２）然るに、「グラフ」を見る限り、当該の患者の、 　　　赤血球とクレアチニンは並行して変化しない。従って、 （３）脱水によって腎機能が悪化している。というわけではない。　　従って、 （４）脱水でないか、　腎機能が悪化していないか、どちらかである。従って、 （５）腎機能が悪化していないか、　脱水でないか、どちらかである。従って （６）腎機能が悪化しているならば、脱水ではない。然るに、 （７）腎機能が悪化している。従って、 （８）脱水ではない（選言三段論法）。

に於いて、

（１）脱水によって腎機能が悪化しているのであれば、赤血球とクレアチニンは 　　　並行して変化しなければならない。 （７）腎機能が悪化している。

という「仮定」は、「真」であるため、

（８）脱水ではない。

という「結論」が「真」であるためには、

（２）赤血球とクレアチニンは並行して変化しない。

という「仮定」が「真」であれば、「十分」である。

従って、

（20）（21）（22）により、

（23）

「赤血球とヘモグロビンとヘマトリック」は、「並行して変化する」が、父の場合は、 「赤血球とクレアチニン」は、「並行して変化する」ということが、全く無かった。

ということを、＃＃先生に、認めて貰えるならば、それだけで、

（８）脱水ではない。

という『診断』が、「確定」します。

 

（1232）「脱水」はなく、それ故、「誤診」である。

― 友人に出そうとして書いたものの、送信しなかったメール ―
（01）
― 省略 ―
（02）
７月８日に送付した「質問書」に対する「回答」が未だに来ないので、
「赤血球」と「クレアチニン」が、「同時に脱水の指標」になることはないのでは？
という内容の「質問」を、改めてするか、しないかを、「検討中」です。
（03）

という「グラフ」を、「赤血球が小さい順」に「並び替える」と、

 

従って、
（03）により、
（04）
「赤血球」と「クレアチニン（Ｃｒｅ）」を、「２つに分ける」と、

従って、
（04）により、
（05）
「２つのグラフ」は、

であるため、「赤血球（脱水の指標）」と「クレアチニン（腎機能の指標）」が、「並行して変動」することはない。
従って、
（06）
「赤血球」の「上昇」があるため、「脱水（血液濃縮）」であって、
「脱水（血液濃縮）」であるが故に、「腎機能が悪化して」いる。
という「事態」には、なってはいない。
従って、
（06）により、
（07）

診療日付　2019年1月27日　12:13 医師カルテ　内科　入院　主保険(0)　 記載者 ＃＃＃

という「診断」は、『誤診』である。

（1231）「象は鼻が長い」の「対偶」の「述語論理」（Ⅱ）。

（01）
１　　　　　（１）∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝　Ａ
　２　　　　（２）∀ｘ｛亀ｘ→∃ｙ（鼻ｙｘ＆～長ｙ）｝　　　　　　　　　　　　　　Ａ
　　３　　　（３）∃ｘ（亀ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　　Ａ
１　　　　　（４）　　　∀ｙ（鼻ｙａ→～長ｙ）∨∃ｚ（～鼻ｚａ＆長ｙ）→～象ａ　　１ＵＥ
　２　　　　（５）　　　亀ａ→∃ｙ（鼻ｙａ＆～長ｙ）　　　　　　　　　　　　　　　２ＵＥ
　　　６　　（６）　　　亀ａ＆象ａ　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　６　　（７）　　　亀ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
　２　６　　（８）　　　　　　∃ｙ（鼻ｙａ＆～長ｙ）　　　　　　　　　　　　　　　５７ＭＰＰ
　　　　９　（９）　　　　　　　　　鼻ｂａ＆～長ｂ　　　　　　　　　　　　　　　　Ａ
　　　　９　（ア）　　　　　　　　　　　　　～長ｂ　　　　　　　　　　　　　　　　９＆Ｅ
　　　６　　（イ）　　　　　　象ａ　　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
　　　６　　（ウ）　　　　～～象ａ　　　　　　　　　　　　　　　　　　　　　　　　イＤＮ
１　　６　　（エ）　～｛∀ｙ（鼻ｙａ→～長ｙ）∨　∃ｚ（～鼻ｚａ＆長ｙ）｝　　　　４ウＭＴＴ
１　　６　　（オ）　　～∀ｙ（鼻ｙａ→～長ｙ）＆～∃ｚ（～鼻ｚａ＆長ｙ）　　　　　エ、ド・モルガンの法則
１　　６　　（カ）　　～∀ｙ（鼻ｙａ→～長ｙ）　　　　　　　　　　　　　　　　　　オ＆Ｅ
１　　６　　（キ）　　∃ｙ～（鼻ｙａ→～長ｙ）　　　　　　　　　　　　　　　　　　カ量化子の関係
　　　　　ク（ク）　　　　～（鼻ｂａ→～長ｂ）　　　　　　　　　　　　　　　　　　Ａ
　　　　　ク（ケ）　　　～（～鼻ｂａ∨～長ｂ）　　　　　　　　　　　　　　　　　　ク含意の定義
　　　　　ク（コ）　　　　　　鼻ｂａ＆　長ｂ　　　　　　　　　　　　　　　　　　　ケ、ド・モルガンの法則
　　　　　ク（サ）　　　　　　　　　　　長ｂ　　　　　　　　　　　　　　　　　　　コ＆Ｅ
　　　　９ク（シ）　　　　　　　～長ｂ＆長ｂ　　　　　　　　　　　　　　　　　　　アサ＆Ｉ
１　　６９　（ス）　　　　　　　～長ｂ＆長ｂ　　　　　　　　　　　　　　　　　　　キクシＥＥ
１２　６　　（セ）　　　　　　　～長ｂ＆長ｂ　　　　　　　　　　　　　　　　　　　８９スＥＥ
１２３　　　（ソ）　　　　　　　～長ｂ＆長ｂ　　　　　　　　　　　　　　　　　　　３６セＥＥ
１２　　　　（タ）～∃ｘ（亀ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　３ソＲＡＡ
１２　　　　（チ）∀ｘ～（亀ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　タ量化子の関係
１２　　　　（ツ）　　～（亀ａ＆象ａ）　　　　　　　　　　　　　　　　　　　　　　チＵＥ
１２　　　　（テ）　　～亀ａ∨～象ａ　　　　　　　　　　　　　　　　　　　　　　　ツ、ド・モルガンの法則
１２　　　　（ト）　　　亀ａ→～象ａ　　　　　　　　　　　　　　　　　　　　　　　テ含意の定義
１２　　　　（ナ）∀ｘ（亀ｘ→～象ｘ）　　　　　　　　　　　　　　　　　　　　　　トＵＩ
従って、
（01）により、
（02）
（ⅰ）∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝。然るに、
（ⅱ）∀ｘ｛亀ｘ→∃ｙ（鼻ｙｘ＆～長ｙ）｝。従って、
（ⅲ）∀ｘ（亀ｘ→～象ｘ）。
といふ「推論（三段論法）」、すなはち、
（ⅰ）すべてのｘについて｛すべてのｙについて（ｙがｘの鼻であるならばｙは長くない）か、または、あるｚについて（ｚがｘの鼻ではなくて長い）ならば、ｘは象ではない｝。然るに、
（ⅱ）すべてのｘについて｛ｘが亀であるならば、あるｙは（ｘの鼻であり、ｙは長くない）｝。　従って、
（ⅲ）すべてのｘについて（ｘが亀であるならば、ｘは象ではない。）
といふ「推論（三段論法）」は、「妥当」である。
従って、
（02）により、
（03）
（ⅰ）鼻が長くないか、鼻以外が長いならば、象ではない。然るに、
（ⅱ）亀の鼻は長くない。従って、
（ⅲ）亀は象ではない。
といふ「推論（三段論法）」は、「妥当」である。
（04）
１　　　　（１）∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝　Ａ
　２　　　（２）∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆　∀ｚ（耳ｚｘ→～鼻ｚｘ）｝　Ａ
　　３　　（３）∃ｘ（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　　Ａ
１　　　　（４）　　　∀ｙ（鼻ｙａ→～長ｙ）∨∃ｚ（～鼻ｚａ＆長ｙ）→～象ａ　　１ＵＥ
　２　　　（５）　　　兎ａ→∃ｙ（長ｙ＆耳ｙａ）＆　∀ｚ（耳ｚａ→～鼻ｚａ）　　２ＵＥ
　　　６　（６）　　　兎ａ＆象ａ　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　６　（７）　　　兎ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
　２　６　（８）　　　　　　∃ｙ（長ｙ＆耳ｙａ）＆　∀ｚ（耳ｚａ→～鼻ｚａ）　　５７ＭＰＰ
　２　６　（９）　　　　　　∃ｙ（長ｙ＆耳ｙａ）　　　　　　　　　　　　　　　　８＆Ｅ
　２　６　（ア）　　　　　　　　　　　　　　　　　　∀ｚ（耳ｚａ→～鼻ｚａ）　　８＆Ｅ
　　　　イ（イ）　　　　　　　　　長ｂ＆耳ｂａ　　　　　　　　　　　　　　　　　Ａ
　２　６　（ウ）　　　　　　　　　　　　　　　　　　　　　耳ｂａ→～鼻ｂａ　　　アＵＥ
　　　　イ（エ）　　　　　　　　　　　　耳ｂａ　　　　　　　　　　　　　　　　　イ＆Ｅ
　２　６イ（オ）　　　　　　　　　　　　　　　　　　　　　　　　　～鼻ｂａ　　　ウエＭＰＰ
　　　　イ（カ）　　　　　　　　　長ｂ　　　　　　　　　　　　　　　　　　　　　イ＆Ｅ
　２　６イ（キ）　　　　　　　　　　　　　　　　　　～鼻ｂａ＆長ｂ　　　　　　　オカ＆Ｉ
　２　６イ（ク）　　　　　　　　　　　　　　　∃ｚ（～鼻ｚａ＆長ｂ）　　　　　　キＥＩ
　２　６　（ケ）　　　　　　　　　　　　　　　∃ｚ（～鼻ｚａ＆長ｂ）　　　　　　９イクＥＥ
　２　６　（コ）　　　∀ｙ（鼻ｙａ→～長ｙ）∨∃ｚ（～鼻ｚａ＆長ｙ）　　　　　　ケ∨Ｉ
１２　６　（サ）　　　　　　　　　　　　　　　　　　　　　　　　　　　～象ａ　　４コＭＰＰ
１２　６　（シ）　　　　　　象ａ　　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
１２　６　（ス）　　　　　　象ａ＆～象ａ　　　　　　　　　　　　　　　　　　　　サシ＆Ｉ
１２３　　（セ）　　　　　　象ａ＆～象ａ　　　　　　　　　　　　　　　　　　　　３６スＥＥ
１２　　　（ソ）～∃ｘ（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　３セＲＡＡ
１２　　　（タ）∀ｘ～（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　ソ量化子の関係
１２　　　（チ）　　～（兎ａ＆象ａ）　　　　　　　　　　　　　　　　　　　　　　タＵＥ
１２　　　（ツ）　　～兎ａ∨～象ａ　　　　　　　　　　　　　　　　　　　　　　　チ、ド・モルガンの法則
１２　　　（テ）　　　兎ａ→～象ａ　　　　　　　　　　　　　　　　　　　　　　　ツ含意の定義
１２　　　（ト）∀ｘ（兎ｘ→～象ｘ）　　　　　　　　　　　　　　　　　　　　　　テＵＩ
従って、
（04）により、
（05）
（ⅰ）∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝。然るに、
（ⅱ）∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆　∀ｚ（耳ｚｘ→～鼻ｚｘ）｝。従って、
（ⅲ）∀ｘ（兎ｘ→～象ｘ）。
といふ「推論（三段論法）」、すなはち、
（ⅰ）すべてのｘについて｛すべてのｙについて（ｙがｘの鼻であるならばｙは長くない）か、または、あるｚについて（ｚがｘの鼻ではなくて長い）ならば、ｘは象ではない｝。然るに、
（ⅱ）すべてのｘについて｛ｘが兎であるならば、あるｙは長くて、ｘの耳であり、すべてのｚについて（ｚがｘの耳であるならば、ｚはｘの鼻ではない）｝。　　　　　　　従って、
（ⅲ）すべてのｘについて（ｘが兎であるならば、ｘは象ではない。）
といふ「推論（三段論法）」は、「妥当」である。
従って、
（05）により、
（06）
（ⅰ）鼻が長くないか、鼻以外が長いならば、象ではない。然るに、
（ⅱ）兎の耳は長いが、耳は鼻ではない。　　　　　　　　従って、
（ⅲ）兎は象ではない。
といふ「推論（三段論法）」は、「妥当」である。
従って、
（01）～（06）により、
（07）
（ⅰ）鼻が長くないか、鼻以外が長いならば、象ではない。然るに、
（ⅱ）亀の鼻は長くないし、
（ⅲ）兎の耳は長いが、耳は鼻ではない。　　　　　　　　従って、
（ⅳ）亀は象ではなく、兎も象ではない。
といふ「推論」は、「妥当」である。
然るに、
（08）
（ⅰ）象は鼻が長い。　　　　　　　　　然るに、
（ⅱ）亀の鼻は長くないし、
（ⅲ）兎の耳は長いが、耳は鼻ではない。従って、
（ⅳ）亀は象ではなく、兎も象ではない。
といふ「推論」も、「妥当」である。
従って、
（07）（08）により、
（09）
① 象は鼻が長い。
② 鼻が長くないか、鼻以外が長いならば、象ではない。
に於いて、
①＝② であるに、違ひない。
然るに、
（10）
（ⅲ）
１　　　　（１）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆　長ｙ）＆　∀ｚ（～鼻ｚｘ→～長ｚ）｝　Ａ
１　　　　（２）　　　象ａ→∃ｙ（鼻ｙａ＆　長ｙ）＆　∀ｚ（～鼻ｚａ→～長ｚ）　　１ＵＥ
　３　　　（３）　　　　　　∀ｙ（鼻ｙａ→～長ｙ）∨　∃ｚ（～鼻ｚａ＆　長ｂ）　　Ａ
　　４　　（４）　　　　　　∀ｙ（鼻ｙａ→～長ｙ）　　　　　　　　　　　　　　　　Ａ
　　４　　（５）　　　　　　　　　鼻ｂａ→～長ｂ　　　　　　　　　　　　　　　　　５ＵＥ
　　４　　（６）　　　　　　　　～鼻ｂａ∨～長ｂ　　　　　　　　　　　　　　　　　５含意の定義
　　４　　（７）　　　　　　　～（鼻ｂａ＆　長ｂ）　　　　　　　　　　　　　　　　６ド・モルガンの法則
　　４　　（８）　　　　　∀ｙ～（鼻ｙａ＆　長ｙ）　　　　　　　　　　　　　　　　７ＵＩ
　　４　　（９）　　　　　～∃ｙ（鼻ｙａ＆　長ｙ）　　　　　　　　　　　　　　　　８量化子の関係
　　４　　（ア）　　　　　～∃ｙ（鼻ｙａ＆　長ｙ）∨～∀ｚ（～鼻ｚａ→～長ｚ）　　９∨Ｉ
　　　５　（イ）　　　　　　　　　　　　　　　　　　　∃ｚ（～鼻ｚａ＆　長ｚ）　　Ａ
　　　　ウ（ウ）　　　　　　　　　　　　　　　　　　　　　　～鼻ｂａ＆　長ｂ　　　Ａ
　　　　ウ（エ）　　　　　　　　　　　　　　　　　　　　　～（鼻ｂａ∨～長ｂ）　　ウ、ド・モルガンの法則
　　　　ウ（オ）　　　　　　　　　　　　　　　　　　　　～（～鼻ｂａ→～長ｂ）　　エ含意の定義
　　　　ウ（カ）　　　　　　　　　　　　　　　　　　∃ｚ～（～鼻ｚａ→～長ｚ）　　オＥＩ
　　　　ウ（キ）　　　　　　　　　　　　　　　　　　～∀ｚ（～鼻ｚａ→～長ｚ）　　カ量化子の関係
　　　　ウ（ク）　　　　　～∃ｙ（鼻ｙａ＆　長ｙ）∨～∀ｚ（～鼻ｚａ→～長ｚ）　　キ∨Ｉ
　３　　　（ケ）　　　　　～∃ｙ（鼻ｙａ＆　長ｙ）∨～∀ｚ（～鼻ｚａ→～長ｚ）　　３４アウク∨Ｅ
　３　　　（コ）　　　　～｛∃ｙ（鼻ｙａ＆　長ｙ）＆　∀ｚ（～鼻ｚｘ→～長ｚ）｝　ケ、ド・モルガンの法則
１３　　　（サ）　　～象ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　　２コＲＡＡ
１　　　　（シ）　　　∀ｙ（鼻ｙａ→～長ｙ）∨∃ｚ（～鼻ｚａ＆　長ｙ）→～象ａ　　３サＣＰ
１　　　　（ス）∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆　長ｚ）→～象ｘ｝　シＵＩ
（ⅳ）
１　　（１）　∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨　∃ｚ（～鼻ｚｘ＆　長ｚ）→～象ｘ｝　Ａ
１　　（２）　　　　∀ｙ（鼻ｙａ→～長ｙ）∨　∃ｚ（～鼻ｚａ＆　長ｙ）→～象ａ　　１ＵＥ
　３　（３）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　象ａ　　Ａ
　３　（４）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　～～象ａ　　３ＤＮ
１３　（５）　　～｛∀ｙ（鼻ｙａ→～長ｙ）∨　∃ｚ（～鼻ｚａ＆　長ｙ）｝　　　　　２４ＭＴＴ
１３　（６）　　　～∀ｙ（鼻ｙａ→～長ｙ）＆～∃ｚ（～鼻ｚａ＆　長ｙ）　　　　　　５ド・モルガンの法則
１３　（７）　　　～∀ｙ（鼻ｙａ→～長ｙ）　　　　　　　　　　　　　　　　　　　　６＆Ｅ
１３　（８）　　　∃ｙ～（鼻ｙａ→～長ｙ）　　　　　　　　　　　　　　　　　　　　７量化子の関係
　　９（９）　　　　　～（鼻ｂａ→～長ｂ）　　　　　　　　　　　　　　　　　　　　Ａ
　　９（ア）　　　　～（～鼻ｂａ∨～長ｂ）　　　　　　　　　　　　　　　　　　　　９含意の定義
　　９（イ）　　　　　　（鼻ｂａ＆　長ｂ）　　　　　　　　　　　　　　　　　　　　ア、ド・モルガンの法則
　　９（ウ）　　　　∃ｙ（鼻ｙａ＆　長ｙ）　　　　　　　　　　　　　　　　　　　　イＥＩ
１３　（エ）　　　　∃ｙ（鼻ｙａ＆　長ｙ）　　　　　　　　　　　　　　　　　　　　８９ウＥＥ
１３　（オ）　　　　　　　　　　　　　　　　～∃ｚ（～鼻ｚａ＆　長ｙ）　　　　　　６＆Ｅ
１３　（カ）　　　　　　　　　　　　　　　　∀ｚ～（～鼻ｚａ＆　長ｙ）　　　　　　オ量化子の関係
１３　（キ）　　　　　　　　　　　　　　　　　　～（～鼻ｂａ＆　長ｂ）　　　　　　カＵＥ
１３　（ク）　　　　　　　　　　　　　　　　　　　～～鼻ｂａ∨～長ｂ　　　　　　　キ、ド・モルガンの法則
１３　（ケ）　　　　　　　　　　　　　　　　　　　　～鼻ｂａ→～長ｂ　　　　　　　ク含意の定義
１３　（コ）　　　　　　　　　　　　　　　　　∀ｚ（～鼻ｚａ→～長ｙ）　　　　　　ケＵＩ
１３　（サ）　　　　　　∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　　　　　エコ＆Ｉ
１　　（シ）　　　象ａ→∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　　　　　３サＣＰ
１　　（ス）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝　　　　　シＵＩ
従って、
（10）により、
（11）
③ ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝
④ ∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝
に於いて、すなはち、
③ すべてのｘについて｛ｘが象であるならば、あるｙはｘの鼻であって、長く、すべてのｚについて（ｚがｘの鼻でないならば、ｚは長くない）｝。
④ すべてのｘについて｛すべてのｙについて（ｙがｘの鼻であるならばｙは長くない）か、または、あるｚについて（ｚがｘの鼻ではなくて長い）ならば、ｘは象ではない｝。
に於いて、
③＝④ は、「対偶」である。
従って、
（09）（10）（11）により、
（12）
① 象は鼻が長い。
② 鼻が長くないか、鼻以外が長いならば、象ではない。
といふ「日本語」は、
① ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝
② ∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝
といふ「意味」であって、
①＝② は、すなはち、
③＝④ は、「対偶」である。

（1230）「象は鼻が長い」の「述語論理」の「対偶」。

（01）
① 象は鼻が長い。
② 象は鼻は長く、鼻以外長くない。
に於いて、
①＝② である。
従って、
（01）により、
（02）
① 象は鼻が長い。
② 鼻が長くないか、または、鼻以外が長いならば、象ではない。
に於いて、
①＝② は、「対偶」である。
然るに、
（03）
１　　　　　（１）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝　Ａ
　２　　　　（２）∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆∀ｚ（耳ｚｘ→～鼻ｚｘ）｝　Ａ
　　３　　　（３）∃ｘ（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　Ａ
１　　　　　（４）　　　象ａ→∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　１ＵＥ
　２　　　　（５）　　　兎ａ→∃ｙ（長ｙ＆耳ｙａ）＆∀ｚ（耳ｚａ→～鼻ｚａ）　　２ＵＥ
　　　６　　（６）　　　兎ａ＆象ａ　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　６　　（７）　　　兎ａ　　　　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
　　　６　　（８）　　　　　　象ａ　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
１　　６　　（９）　　　　　　∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　４８ＭＰＰ
　２　６　　（ア）　　　　　　∃ｙ（長ｙ＆耳ｙａ）＆∀ｚ（耳ｚａ→～鼻ｚａ）　　５７ＭＰＰ
１　　６　　（イ）　　　　　　∃ｙ（鼻ｙａ＆長ｙ）　　　　　　　　　　　　　　　９＆Ｅ
　　　　ウ　（ウ）　　　　　　　　　鼻ｂａ＆長ｂ　　　　　　　　　　　　　　　　Ａ
　２　６　　（エ）　　　　　　∃ｙ（長ｙ＆耳ｙａ）　　　　　　　　　　　　　　　ア＆Ｅ
　　　　　オ（オ）　　　　　　　　　長ｂ＆耳ｂａ　　　　　　　　　　　　　　　　Ａ
　　　　　オ（カ）　　　　　　　　　　　　耳ｂａ　　　　　　　　　　　　　　　　オ＆Ｅ
１　　６　　（キ）　　　　　　　　　　　　　　　　　∀ｚ（～鼻ｚａ→～長ｚ）　　９＆Ｅ
　２　６　　（ク）　　　　　　　　　　　　　　　　　∀ｚ（耳ｚａ→～鼻ｚａ）　　ア＆Ｅ
１　　６　　（ケ）　　　　　　　　　　　　　　　　　　　　～鼻ｂａ→～長ｂ　　　キＵＥ
　２　６　　（コ）　　　　　　　　　　　　　　　　　　　　耳ｂａ→～鼻ｂａ　　　クＵＥ
　２　６　オ（サ）　　　　　　　　　　　　　　　　　　　　　　　　～鼻ｂａ　　　カコＭＰＰ
１２　６　オ（シ）　　　　　　　　　　　　　　　　　　　　　　　　　～長ｂ　　　ケサＭＰＰ
　　　　　オ（ス）　　　　　　　　　長ｂ　　　　　　　　　　　　　　　　　　　　オ＆Ｅ
１２　６　オ（セ）　　　　　　　　　長ｂ＆～長ｂ　　　　　　　　　　　　　　　　シス＆Ｉ
１２　６　　（ソ）　　　　　　　　　長ｂ＆～長ｂ　　　　　　　　　　　　　　　　エオセＥＥ
１２３　　　（タ）　　　　　　　　　長ｂ＆～長ｂ　　　　　　　　　　　　　　　　３６ソＥＥ
１２　　　　（チ）～∃ｘ（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　３タＲＡＡ
１２　　　　（ツ）∀ｘ～（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　チ量化子の関係
１２　　　　（テ）　　～（兎ａ＆象ａ）　　　　　　　　　　　　　　　　　　　　　ツＵＥ
１２　　　　（ト）　　～兎ａ∨～象ａ　　　　　　　　　　　　　　　　　　　　　　テ、ド・モルガンの法則
１２　　　　（ナ）　　　兎ａ→～象ａ　　　　　　　　　　　　　　　　　　　　　　ト含意の定義
１２　　　　（ニ）∀ｘ（兎ｘ→～象ｘ）　　　　　　　　　　　　　　　　　　　　　ナＵＩ
従って、
（03）により、
（04）
（ⅰ）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。然るに、
（ⅱ）∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆∀ｚ（耳ｚｘ→～鼻ｚｘ）｝。従って、
（ⅲ）∀ｘ（兎ｘ→～象ｘ）。
といふ「推論（三段論法）」、すなはち、
（ⅰ）すべてのｘについて｛ｘが象であるならば、あるｙはｘの鼻であって、長く、すべてのｚについて（ｚがｘの鼻でないならば、ｚは長くない）｝。　　　然るに、
（ⅱ）すべてのｘについて｛ｘが兎であるならば、あるｙは長くて、ｘの耳であり、すべてのｚについて（ｚがｘの耳であるならば、ｚはｘの鼻ではない）｝。従って、
（ⅲ）すべてのｘについて（ｘが兎であるならば、ｘは象ではない。）
といふ「推論（三段論法）」は、「妥当」である。
従って、
（04）により、
（05）
（ⅰ）象は鼻が長い。然るに、
（ⅱ）兎の耳は長いが、耳は鼻ではない。従って、
（ⅲ）兎は象ではない。
といふ「推論（三段論法）」は、「妥当」である。
従って、
（03）（04）（05）により、
（06）
① 象は鼻が長い。
といふ「日本語」は、
① ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。
といふ「述語論理式」に「等しい」。
従って、
（03）（06）により、
（07）
① ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝。
② 鼻が長くないか、または、鼻以外が長いならば、象ではない。
に於いて、
①＝② は、「対偶」である。
然るに、
（08）
（ⅰ）
１　　　　（１）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆　長ｙ）＆　∀ｚ（～鼻ｚｘ→～長ｚ）｝　Ａ
１　　　　（２）　　　象ａ→∃ｙ（鼻ｙａ＆　長ｙ）＆　∀ｚ（～鼻ｚａ→～長ｚ）　　１ＵＥ
　３　　　（３）　　　　　　∀ｙ（鼻ｙａ→～長ｙ）∨　∃ｚ（～鼻ｚａ＆　長ｂ）　　Ａ
　　４　　（４）　　　　　　∀ｙ（鼻ｙａ→～長ｙ）　　　　　　　　　　　　　　　　Ａ
　　４　　（５）　　　　　　　　　鼻ｂａ→～長ｂ　　　　　　　　　　　　　　　　　５ＵＥ
　　４　　（６）　　　　　　　　～鼻ｂａ∨～長ｂ　　　　　　　　　　　　　　　　　５含意の定義
　　４　　（７）　　　　　　　～（鼻ｂａ＆　長ｂ）　　　　　　　　　　　　　　　　６ド・モルガンの法則
　　４　　（８）　　　　　∀ｙ～（鼻ｙａ＆　長ｙ）　　　　　　　　　　　　　　　　７ＵＩ
　　４　　（９）　　　　　～∃ｙ（鼻ｙａ＆　長ｙ）　　　　　　　　　　　　　　　　８量化子の関係
　　４　　（ア）　　　　　～∃ｙ（鼻ｙａ＆　長ｙ）∨～∀ｚ（～鼻ｚａ→～長ｚ）　　９∨Ｉ
　　　５　（イ）　　　　　　　　　　　　　　　　　　　∃ｚ（～鼻ｚａ＆　長ｚ）　　Ａ
　　　　ウ（ウ）　　　　　　　　　　　　　　　　　　　　　　～鼻ｂａ＆　長ｂ　　　Ａ
　　　　ウ（エ）　　　　　　　　　　　　　　　　　　　　　～（鼻ｂａ∨～長ｂ）　　ウ、ド・モルガンの法則
　　　　ウ（オ）　　　　　　　　　　　　　　　　　　　　～（～鼻ｂａ→～長ｂ）　　エ含意の定義
　　　　ウ（カ）　　　　　　　　　　　　　　　　　　∃ｚ～（～鼻ｚａ→～長ｚ）　　オＥＩ
　　　　ウ（キ）　　　　　　　　　　　　　　　　　　～∀ｚ（～鼻ｚａ→～長ｚ）　　カ量化子の関係
　　　　ウ（ク）　　　　　～∃ｙ（鼻ｙａ＆　長ｙ）∨～∀ｚ（～鼻ｚａ→～長ｚ）　　キ∨Ｉ
　３　　　（ケ）　　　　　～∃ｙ（鼻ｙａ＆　長ｙ）∨～∀ｚ（～鼻ｚａ→～長ｚ）　　３４アウク∨Ｅ
　３　　　（コ）　　　　～｛∃ｙ（鼻ｙａ＆　長ｙ）＆　∀ｚ（～鼻ｚｘ→～長ｚ）｝　ケ、ド・モルガンの法則
１３　　　（サ）　　～象ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　　２コＲＡＡ
１　　　　（シ）　　　∀ｙ（鼻ｙａ→～長ｙ）∨∃ｚ（～鼻ｚａ＆　長ｙ）→～象ａ　　３サＣＰ
１　　　　（ス）∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆　長ｚ）→～象ｘ｝　シＵＩ
（ⅱ）
１　　（１）　∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨　∃ｚ（～鼻ｚｘ＆　長ｚ）→～象ｘ｝　Ａ
１　　（２）　　　　∀ｙ（鼻ｙａ→～長ｙ）∨　∃ｚ（～鼻ｚａ＆　長ｙ）→～象ａ　　１ＵＥ
　３　（３）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　象ａ　　Ａ
　３　（４）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　～～象ａ　　３ＤＮ
１３　（５）　　～｛∀ｙ（鼻ｙａ→～長ｙ）∨　∃ｚ（～鼻ｚａ＆　長ｙ）｝　　　　　２４ＭＴＴ
１３　（６）　　　～∀ｙ（鼻ｙａ→～長ｙ）＆～∃ｚ（～鼻ｚａ＆　長ｙ）　　　　　　５ド・モルガンの法則
１３　（７）　　　～∀ｙ（鼻ｙａ→～長ｙ）　　　　　　　　　　　　　　　　　　　　６＆Ｅ
１３　（８）　　　∃ｙ～（鼻ｙａ→～長ｙ）　　　　　　　　　　　　　　　　　　　　７量化子の関係
　　９（９）　　　　　～（鼻ｂａ→～長ｂ）　　　　　　　　　　　　　　　　　　　　Ａ
　　９（ア）　　　　～（～鼻ｂａ∨～長ｂ）　　　　　　　　　　　　　　　　　　　　９含意の定義
　　９（イ）　　　　　　（鼻ｂａ＆　長ｂ）　　　　　　　　　　　　　　　　　　　　ア、ド・モルガンの法則
　　９（ウ）　　　　∃ｙ（鼻ｙａ＆　長ｙ）　　　　　　　　　　　　　　　　　　　　イＥＩ
１３　（エ）　　　　∃ｙ（鼻ｙａ＆　長ｙ）　　　　　　　　　　　　　　　　　　　　８９ウＥＥ
１３　（オ）　　　　　　　　　　　　　　　　～∃ｚ（～鼻ｚａ＆　長ｙ）　　　　　　６＆Ｅ
１３　（カ）　　　　　　　　　　　　　　　　∀ｚ～（～鼻ｚａ＆　長ｙ）　　　　　　オ量化子の関係
１３　（キ）　　　　　　　　　　　　　　　　　　～（～鼻ｂａ＆　長ｂ）　　　　　　カＵＥ
１３　（ク）　　　　　　　　　　　　　　　　　　　～～鼻ｂａ∨～長ｂ　　　　　　　キ、ド・モルガンの法則
１３　（ケ）　　　　　　　　　　　　　　　　　　　　～鼻ｂａ→～長ｂ　　　　　　　ク含意の定義
１３　（コ）　　　　　　　　　　　　　　　　　∀ｚ（～鼻ｚａ→～長ｙ）　　　　　　ケＵＩ
１３　（サ）　　　　　　∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　　　　　エコ＆Ｉ
１　　（シ）　　　象ａ→∃ｙ（鼻ｙａ＆長ｙ）＆∀ｚ（～鼻ｚａ→～長ｚ）　　　　　　３サＣＰ
１　　（ス）∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆∀ｚ（～鼻ｚｘ→～長ｚ）｝　　　　　シＵＩ
従って、
（08）により、
（09）
① ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆  ∀ｚ（～鼻ｚｘ→～長ｚ）｝
② ∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝
に於いて、
①＝② である。
然るに、
（10）
１　　　　（１）∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝　Ａ
　２　　　（２）∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆　∀ｚ（耳ｚｘ→～鼻ｚｘ）｝　Ａ
　　３　　（３）∃ｘ（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　　Ａ
１　　　　（４）　　　∀ｙ（鼻ｙａ→～長ｙ）∨∃ｚ（～鼻ｚａ＆長ｙ）→～象ａ　　１ＵＥ
　２　　　（５）　　　兎ａ→∃ｙ（長ｙ＆耳ｙａ）＆　∀ｚ（耳ｚａ→～鼻ｚａ）　　２ＵＥ
　　　６　（６）　　　兎ａ＆象ａ　　　　　　　　　　　　　　　　　　　　　　　　Ａ
　　　６　（７）　　　兎ａ　　　　　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
　２　６　（８）　　　　　　∃ｙ（長ｙ＆耳ｙａ）＆　∀ｚ（耳ｚａ→～鼻ｚａ）　　５７ＭＰＰ
　２　６　（９）　　　　　　∃ｙ（長ｙ＆耳ｙａ）　　　　　　　　　　　　　　　　８＆Ｅ
　２　６　（ア）　　　　　　　　　　　　　　　　　　∀ｚ（耳ｚａ→～鼻ｚａ）　　８＆Ｅ
　　　　イ（イ）　　　　　　　　　長ｂ＆耳ｂａ　　　　　　　　　　　　　　　　　Ａ
　２　６　（ウ）　　　　　　　　　　　　　　　　　　　　　耳ｂａ→～鼻ｂａ　　　アＵＥ
　　　　イ（エ）　　　　　　　　　　　　耳ｂａ　　　　　　　　　　　　　　　　　イ＆Ｅ
　２　６イ（オ）　　　　　　　　　　　　　　　　　　　　　　　　　～鼻ｂａ　　　ウエＭＰＰ
　　　　イ（カ）　　　　　　　　　長ｂ　　　　　　　　　　　　　　　　　　　　　イ＆Ｅ
　２　６イ（キ）　　　　　　　　　　　　　　　　　　～鼻ｂａ＆長ｂ　　　　　　　オカ＆Ｉ
　２　６イ（ク）　　　　　　　　　　　　　　　∃ｚ（～鼻ｚａ＆長ｂ）　　　　　　キＥＩ
　２　６　（ケ）　　　　　　　　　　　　　　　∃ｚ（～鼻ｚａ＆長ｂ）　　　　　　９イクＥＥ
　２　６　（コ）　　　∀ｙ（鼻ｙａ→～長ｙ）∨∃ｚ（～鼻ｚａ＆長ｙ）　　　　　　ケ∨Ｉ
１２　６　（サ）　　　　　　　　　　　　　　　　　　　　　　　　　　　～象ａ　　４コＭＰＰ
１２　６　（シ）　　　　　　象ａ　　　　　　　　　　　　　　　　　　　　　　　　６＆Ｅ
１２　６　（ス）　　　　　　象ａ＆～象ａ　　　　　　　　　　　　　　　　　　　　サシ＆Ｉ
１２３　　（セ）　　　　　　象ａ＆～象ａ　　　　　　　　　　　　　　　　　　　　３６スＥＥ
１２　　　（ソ）～∃ｘ（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　３セＲＡＡ
１２　　　（タ）∀ｘ～（兎ｘ＆象ｘ）　　　　　　　　　　　　　　　　　　　　　　ソ量化子の関係
１２　　　（チ）　　～（兎ａ＆象ａ）　　　　　　　　　　　　　　　　　　　　　　タＵＥ
１２　　　（ツ）　　～兎ａ∨～象ａ　　　　　　　　　　　　　　　　　　　　　　　チ、ド・モルガンの法則
１２　　　（テ）　　　兎ａ→～象ａ　　　　　　　　　　　　　　　　　　　　　　　ツ含意の定義
１２　　　（ト）∀ｘ（兎ｘ→～象ｘ）　　　　　　　　　　　　　　　　　　　　　　テＵＩ
従って、
（10）により、
（11）
（ⅰ）∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝。然るに、
（ⅱ）∀ｘ｛兎ｘ→∃ｙ（長ｙ＆耳ｙｘ）＆　∀ｚ（耳ｚｘ→～鼻ｚｘ）｝。従って、
（ⅲ）∀ｘ（兎ｘ→～象ｘ）。
といふ「推論（三段論法）」、すなはち、
（ⅰ）すべてのｘについて｛すべてのｙについて（ｙがｘの鼻であるならばｙは長くない）か、または、あるｚについて（ｚがｘの鼻ではなくて長い）ならば、ｘは象ではない｝。然るに、
（ⅱ）すべてのｘについて｛ｘが兎であるならば、あるｙは長くて、ｘの耳であり、すべてのｚについて（ｚがｘの耳であるならば、ｚはｘの鼻ではない）｝。　　　　　　　従って、
（ⅲ）すべてのｘについて（ｘが兎であるならば、ｘは象ではない。）
といふ「推論（三段論法）」は、「妥当」である。
従って、
（11）により、
（12）
（ⅰ）鼻が長くないか、鼻以外が長いならば、象ではない。然るに、
（ⅱ）兎の耳は長いが、耳は鼻ではない。　　　　　　　　従って、
（ⅲ）兎は象ではない。
といふ「推論（三段論法）」は、「妥当」である。
従って、
（10）（11）（12）により、
（13）
② 鼻が長くないか、鼻以外が長いならば、象ではない。
といふ「日本語」は、
② ∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝。
といふ「述語論理式」に「等しい」。
従って、
（01）～（13）により、
（14）
① 象は鼻が長い。
② 鼻が長くないか、鼻以外が長いならば、象ではない。
といふ「日本語」は、
① ∀ｘ｛象ｘ→∃ｙ（鼻ｙｘ＆長ｙ）＆  ∀ｚ（～鼻ｚｘ→～長ｚ）｝
② ∀ｘ｛∀ｙ（鼻ｙｘ→～長ｙ）∨∃ｚ（～鼻ｚｘ＆長ｚ）→～象ｘ｝
に於いて、
①＝② は、「対偶」である。
然るに、
（15）
現生のゾウの類縁だが、直接の祖先ではない。約400万年前から1万年前頃（絶滅時期は諸説ある）までの期間に生息していた。巨大な牙が特徴で、種類によっては牙の長さが5.2メートルに達することもある（ウィキペディア）といふことからすれば、「（マンモス）象は、牙も長い。」
従って、
（14）（15）により、
（16）
① 兎は耳が長い。
② 耳が長くないか、耳以外が長いならば、兎ではない。
といふ「日本語」は、
① ∀ｘ｛兎ｘ→∃ｙ（耳ｙｘ＆長ｙ）＆  ∀ｚ（～耳ｚｘ→～長ｚ）｝
② ∀ｘ｛∀ｙ（耳ｙｘ→～長ｙ）∨∃ｚ（～耳ｚｘ＆長ｚ）→～兎ｘ｝
に於いて、
①＝② は、 「対偶」である。
とした方が、「適切」である。
従って、
（06）（13）（16）により、
（17）
（ⅰ）兎は耳が長い。然るに、
（ⅱ）象の鼻は長いが、鼻は耳ではない。従って、
（ⅲ）象は兎ではない。
といふ「推論（三段論法）」、並びに、
（ⅰ）耳が長くないか、耳以外が長いならば、兎ではない。然るに、
（ⅱ）象の鼻は長いが、鼻は耳ではない。　　　　　　　　従って、
（ⅲ）象は兎ではない。
といふ「推論（三段論法）」は、「妥当」である。
とするためには、
① 兎は耳が長い。
② 耳が長くないか、耳以外が長いならば、兎ではない。
といふ「日本語」は、
① ∀ｘ｛兎ｘ→∃ｙ（耳ｙｘ＆長ｙ）＆  ∀ｚ（～耳ｚｘ→～長ｚ）｝
② ∀ｘ｛∀ｙ（耳ｙｘ→～長ｙ）∨∃ｚ（～耳ｚｘ＆長ｚ）→～兎ｘ｝
といふ「意味」であるが故に、
①＝② でなければ、ならない。
然るに、
（18）
沢田充茂の『現代論理学入門』（一九六ニ年）には楽しい解説が載っています。
・・・・・・たとえば「象は鼻が長い」というような表現は、象が主語なのか、鼻が主語なのかはっきりしないから、このままではその論理的構造が明示されていない。いわば非論理的な文章である、というひともある。しかしこの文の論理的な構造をはっきりと文章にあらわして「すべてのｘについて、もしそのｘが象であるならば、ｙなるものが存在し、そのｙは鼻であり、ｘはｙを所有しており、このｙは長い」といえば・・・・・・たとえば動物園で象をはじめて見た小学生が、父親にむかってこのような文章で話しかけたとすれば、その子供は論理的であるといって感心されるまえに社会人としての常識をうたがわれるにきまっている。常識（すなはち共通にもっている情報）でわかっているものはいちいち言明の中にいれないで、いわば暗黙の了解事項として、省略し、できるだけ短い記号の組み合せで、できるだけ多くの情報を伝えることが日常言語の合理性の一つである。・・・・・・
（山崎紀美子、日本語基礎講座―三上文法入門、2003年、２１４頁）
然るに、
（18）により、
（19）
「すべてのｘについて、もしそのｘが象であるならば、ｙなるものが存在し、そのｙは鼻であり、ｘはｙを所有しており、このｙは長い」といえば、
① ∀ｘ｛兎ｘ→∃ｙ（耳ｙｘ＆長ｙ）＆ ∀ｚ（～耳ｚｘ→～長ｚ）｝
といふ「意味」ではなく、
① ∀ｘ｛兎ｘ→∃ｙ（耳ｙｘ＆長ｙ）｝
といふ「意味」である。
従って、
（04）（05）（15）（19）により、
（20）
「象は鼻が長い。」といふ「日本語」が、
「すべてのｘについて、もしそのｘが象であるならば、ｙなるものが存在し、そのｙは鼻であり、ｘはｙを所有しており、このｙは長い。」
といふ「意味」であるならば、
（ⅰ）象は鼻が長い。然るに、
（ⅱ）兎の耳は長いが、耳は鼻ではない。従って、
（ⅲ）兎は象ではない。
といふ「推論（三段論法）」は、「妥当」ではない。
（21）
沢田充茂の『現代論理学入門』（一九六ニ年）に、
① ∀ｘ｛兎ｘ→∃ｙ（耳ｙｘ＆長ｙ）＆ ∀ｚ（～耳ｚｘ→～長ｚ）｝
といふ「述語論理式」が、載ってゐなかったことを、私は、極めて、残念に思ふ。

（1229）「脱水」ではない（Ⅱ）。

（01）
Ｐ＝０（偽）
Ｑ＝１（真）
Ｒ＝１（真）
のとき、
①  ０→（１→１）＝１（真）
②（１→１）→０　＝０（偽）
従って、
（01）により、
（02）
①  Ｐ→（Ｑ→Ｒ）
②（Ｑ→Ｒ）→Ｐ
に於いて、
① が「真（１）」であったとしても、
② も「真（１）」であるとは、「限らない」。
然るに、
（03）
１　　　（１）　Ｐ→（Ｑ→　Ｒ）　Ａ
　２　　（２）　　　　Ｑ＆～Ｒ　　Ａ
　　３　（３）　　　　Ｑ→　Ｒ　　Ａ
　２　　（４）　　　　Ｑ　　　　　２＆Ｅ
　２３　（５）　　　　　　　Ｒ　　３４ＭＰＰ
　２　　（６）　　　　　　～Ｒ　　２＆Ｅ
　２３　（７）　　　　Ｒ＆～Ｒ　　５６＆Ｉ
　２　　（８）　　～（Ｑ→　Ｒ）　３７ＲＡＡ
１２　　（９）～Ｐ　　　　　　　　１８ＭＴＴ
１　　　（ア）（Ｑ＆～Ｒ）→～Ｐ　２９ＣＰ
　　　イ（イ）　　　　　　　　Ｐ　Ａ
　　　イ（ウ）　　　　　　～～Ｐ　イＤＮ
１　　イ（エ）　～（Ｑ＆～Ｒ）　　アウＭＴＴ
１　　イ（オ）　　～Ｑ∨　Ｒ　　　エ、ド・モルガンの法則
１　　イ（カ）　　　Ｑ→　Ｒ　　　オ含意の定義
１　　　（キ）Ｐ→（Ｑ→　Ｒ）　　イカＣＰ
従って、
（03）により、
（04）
①  Ｐ→（Ｑ→Ｒ）
③（Ｑ＆～Ｒ）→～Ｐ
に於いて、
①＝③ である。
従って、
（02）（04）により、
（05）
①  Ｐ→（Ｑ→Ｒ）
②（Ｑ→Ｒ）→Ｐ
③（Ｑ＆～Ｒ）→～Ｐ
に於いて、
①≠② は、「（対偶ではなく）逆」であり、
①＝③ は、「（逆ではなく）対偶」である。
然るに、
（06）
① Ｐ→（Ｑ→Ｒ）
に於いて、
Ｐ＝脱水である。
Ｑ＝点滴をする。
Ｒ＝数値が下がる。
という「代入」を行うと、
① Ｐ→（Ｑ→Ｒ）
という「命題」は、
① 脱水であるならば（点滴をすると、数値は下がる）。
という「命題」に「等しい」。
従って、
（05）（06）により、
（07）
①  脱水であるならば（点滴をすると、数値は下がる）。
②（点滴をすると、数値は下がる）ならば脱水である。
③（点滴しても、数値が下がらない）ならば脱水ではない。
に於いて、
①＝② ではないが、
①＝③ である。
従って、
（07）により、
（08）
① 脱水であるならば（点滴をすると、数値は下がる）。
という「命題」が「真」である際に、
② 点滴をすると、数値は下がった。　　　従って、脱水であった。
③ 点滴しても、数値は下がらなかった。従って、脱水ではなかった。
に於いて、
② は、「確率的に、妥当」であるが、
③ は、「必然的に、妥当」である。
従って、
（08）により、
（09）
① 脱水であっても、点滴をすると、数値は下がるし、
② 脱水でなくとも、点滴をすると、数値は下がるが、
③ 点滴をしても、数値が下がらないならば、脱水ではない。
という、ことになる。
然るに、
（10）

従って、
（10）により、
（11）
「赤血球・ヘモグロビン・ヘマトリック」の「３項目」は「平行して変動」することが「多い」が、
「ヘモグロビン」が「特に高い」場合は、「多血症」のようである。
然るに、
（12）

従って、
（11）（12）により、
（13）
「基本的」には、
「赤血球・ヘモグロビン・ヘマトリック」だけでなく、
「アルブミン・総蛋白・尿酸・Ｃｒｅ・ＢＵＮ」も「平行して変動」することが「多い」が、
「Ｃｒｅ・ＢＵＮ」が「特に高い」場合は、
「Ｃｒｅ・ＢＵＮ」が「特に高い」場合に多い「腎機能の低下（急性腎不全）」である。
という、ことになる。
従って、
（09）（13）により、
（14）
① 脱水であっても、点滴をすると、数値は下がるし、
② 脱水でなくとも、点滴をすると、数値は下がるが、
③ 点滴をしても、数値が下がらないならば、脱水ではない。
という、ことになり、
「アルブミン・総蛋白・尿酸・Ｃｒｅ・ＢＵＮ」も「平行して変動」することが「多い」が、
「Ｃｒｅ・ＢＵＮ」が「特に高い」場合は、
「Ｃｒｅ・ＢＵＮ」が「特に高い」場合に多い「腎機能の低下（急性腎不全）」である。
という、ことになる。
従って、
（14）により、
（15）

という「結果」は、「急性腎不全」を示している。

（1228）脱水ではない！！

（01）

従って、
（01）により、
（02）
Ｓ医師は、
「点滴」によって「血液が希釈」されれば、
「赤血球・Ｈｂ・Ｈｔ・ナトリウム・アルブミン・総蛋白・尿酸・Ｃｒｅ・ＢＵＮ」の「各値」は「下降」し、
「点滴」を「中断」すれば「血液が濃縮」され、
「赤血球・Ｈｂ・Ｈｔ・ナトリウム・アルブミン・総蛋白・尿酸・Ｃｒｅ・ＢＵＮ」の「各値」は「上昇」する。
という風に、『診断』している。
然るに、
（03）

従って、
（03）により、
（04）

従って、
（04）により、
（05）
「２０１９年０１月１８日」から、
「２０１９年０１月２５日」にかけて、「点滴」を「中止」したところ、
「赤血球・尿酸」等は、「１.３倍弱」に増加したが、
「クレアチニン」は、「１.７３倍」になり、
「尿素窒素（ＢＵＮ）」に至っては、「３倍以上」になっているが、
「２０１９年０１月２５日」にかけて、「点滴」を「再開」した後も、
「２０１９年０１月２９日」に於いて、「数値」は、「改善」されていない。
従って、
（01）～（05）により、
（06）
Ｓ医師による、

という『診断』は、明らかな「誤診」である。
然るに、
（07）
患者に対して医師が薬を投与したときに、蕁麻疹が生じる等の症状が出たときには、薬の副作用の疑いもあります。このとき、同じ薬を投与し続ければ、さらに重い副作用が発生して深刻な影響が生じることを予見し、薬の投与を中断したり、薬の種類を変更したりして、深刻な影響が生じるという結果を回避できる場合があります。このような予見可能性と結果回避可能性は、注意義務違反（過失）の前提として必要とされるものです（医学博士 弁護士 金﨑浩之）。
従って、
（07）により、
（08）
『誤診』により、「患者が死亡した場合」であったとしても、
「予見」が「不可能」である場合には、医師には、責任が無い。
然るに、
（09）

然るに、
（09）により、
（10）
「グラフ（09）」の「赤血球の値」を、「小さい順」に並べると、

従って、
（10）により、
（11）
「グラフ（10）」を「２つに分ける」と、

従って、
（11）により、
（12）
「赤血球の値」を「小さい順」に並べると、
「Ｃｒｅ（同じ日付）」は、「小さい順」ではなく、「ランダムに並ぶ」ものの、
このことは、少なくとも、「当該の患者」の場合は、
「赤血球の値」は、「Ｃｒｅの値」に、「影響」を与えないし、
「Ｃｒｅの値」は、「赤血球の値」に、「影響」を与えない。
ということを、示している。
従って、
（03）（09）（12）により、
（13）

という「データ」に於ける、
「２０１９年１２月２５日」の「数値」に「注意」を向けていたとすれば、
「２０１９年１２月２９日」の「結果」を「予想」出来なかった、とは言えないはずであるし、
「患者」は、「悪性貧血」と「慢性腎臓病」が、「持病」であったため、
「赤血球」と「クレアチニン（Ｃｒｅ）」の「値」には、特別に、「注意」をすべきであった。
従って、
（08）（13）により、
（14）
『誤診』により、「患者が死亡した場合」であったとしても、
「予見」が「不可能」である場合には、医師には、責任が無い。
とは言うものの、この場合は、「予見」は、「不可能」であったとは、言えない。
従って、
（14）により、
（15）
Ｓ医師は、患者の保護者である私の承諾を得ずに、「予防」と称して、勝手に投与を開始した、

 

　　　　　　　　　　　　　　　　　　　　（２０１２年０７月０５日、Ｋ医師）
でいう所の、「禁忌薬剤の投与」を、ただちに「中止」すべきであったし、そもそも、「投与」自体が「不要」であったっため、

という「診療」が、「妥当」であった。
とは、とうてい言えない。
（16）
医療行為は、患者さんにとってもリスクのあるものですが、医者にとってもリスクがあるものです。良かれと思ってやっていても、患者が亡くなってしまえば、訴えられたり、逮捕されたりすることあります。患者さんの御遺族もつらい思いをしますが、医者の側も、非常につらく、苦しい人生が始まってしまいます（渡邊剛、医者になる人に知っておいてほしいこと、2012年、１９頁）。
とは言うものの、『誤診』自体は、「罪」にはならないし、いろいろと、図書館にある本を読んでみても、「そうとういいかげんの医師」でなければ、実際には、医師が有罪になることはない。

（1227）「点滴」と「脱水」と「逆」と「対偶」。

（01）
赤血球が増える場合には、見かけ上の場合は、血液が濃縮されることによって起こります。例えば暑い場所で運動するなどして脱水状態を起こし、血液の濃度が上がる場合（検査と病気の関係：赤血球 ヘマトクリット ヘモグロビン）。
然るに、
（02）

従って、
（01）（02）により、
（03）
（ⅰ）「脱水」が有る場合は、　　「血液が濃縮され」、「血液が濃縮され」ると、「赤血球の値が上昇」する。
（ⅱ）「点滴（輸液）」を行うと、「血液が希釈され」、「血液が希釈され」ると、「赤血球の値が低下」する。
然るに、
（04）
●基準値
検査施設によっても異なりますが、赤血球数は、男性では1マイクロリットルのなかに420～570万個、女性では380～500万個。ヘマトクリットは男性では40～52％、女性では33～45％。ヘモグロビンは男性が1デシリットルのなかに13.5～18g、女性では11.5～16g程度です。超高齢者（80歳以上）の場合は若干数値を低めに見積もる方がいいでしょう。ちなみにヘモグロビンとヘマトクリットは平行して変動します（赤血球　ヘマトクリット　ヘモグロビン）。
然るに、

（05）

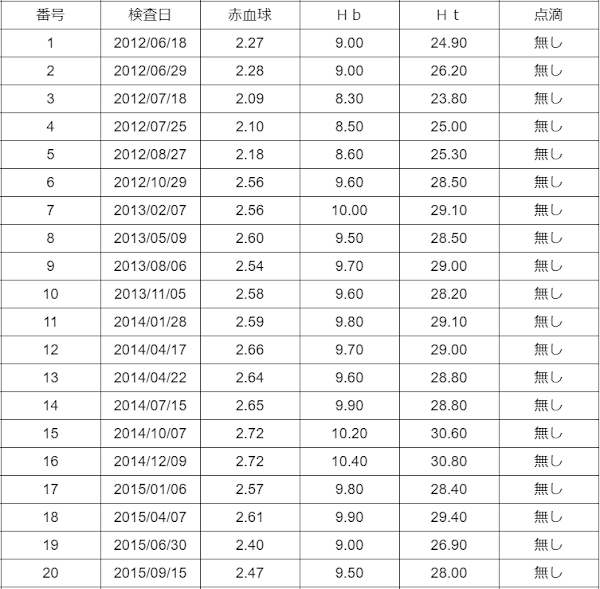従って、
（06）
「２０１２年０６月１８日」から、
「２０１９年０１月２９日」まで（計４１回）の、
「赤血球・ヘモグロビン・ヘマトリックの推移」を「グラフ」で見ると、

（04）（05）（06）により、
（07）
この場合は、「ヘモグロビン（Ｈｂ）と「ヘマトリック（Ｈｔ）」だけでなく、
「赤血球とヘモグロビン（Ｈｂ）とヘマトリック（Ｈｔ）の３つが平行して変動している。」
然るに、
（05）（06）（07）により、
（08）
「赤血球・ヘモグロビン・ヘマトリック」の「平均値」が「同じ値」になるように「掛け算」をした「結果」を「大きい順」に並べると、

従って、
（08）により、
（09）
「４１回の検査」の内、「値の大きい順に並べた」際に、
「３７～４１番（下位の５番以内）」は全て、「点滴有り」である。
然るに、
（10）
　次に示す「２つ順列」は、
『仮説検定』を行う上での、「確率」と関係があります。
（ａ）

（ｂ）

従って、
（10）により、
（11）
男子＝｛Ａ，Ｂ，Ｃ｝
女子＝｛Ｄ，Ｅ｝
であるとして、 男子と女子が、「くじ引き」で、「１列」に並ぶ際に、
女子＝｛Ｄ，Ｅ｝
の「２人」が、「４番目と５番目に並ぶ、確率」は、
（３！×２！）÷５！＝１２÷１２０＝０.１
であって、
女子＝｛Ｄ，Ｅ｝
の内の「（どちらか）１人」が「５番目に並ぶ、確率」は、
（４！×２！）÷５！＝４８÷１２０＝０.４
である。
従って、
（10）（11）により、
（12）
「男子３６人、女子５人の、４１人の生徒」が、「ランダム」に
「一列に並ぶ際」に、「女子５人」が「最後の５人」になる「確率Ｐ」は、
（３６！×５！）÷４１！≒（７５万分の１）≒０.０００００１３３
である。
従って、
（12）により、
（13）
「点滴無し（３６個）、点滴有り（５個）の、４１個のデータ」を、「ランダム」に
「一列に並べる際」に、点滴有り（５個）が「最後の５個」になる「確率Ｐ」も、
（３６！×５！）÷４１！≒（７５万分の１）≒０.０００００１３３
である。
然るに、
（14）
① ０.０５
② ０.０００００１３３
に於いて、
② の方が、① よりも、「極端に、小さい」。
然るに、
（15）
Ｐ＜０.０５は慣習的なものだ。Ｐ＜０.０５を有意水準とする数学的な根拠は無くて、
Ｐ＜０.１でもＰ＜０.０３でも構わないが、Ｐ＜０.０５以外を有意水準にするときは、
根拠を問われることになる（Ｐ値と有意水準 | ブログ | 統計WEB）。
従って、
（13）（14）（15）により、
（16）
「（ただ単に）習慣」として、
「０．０５」　　　　　　という「Ｐ値」が、「まれな値」であるならば、
「０．０００００１３３」という「Ｐ値」は、なおのこと「非常にまれな値」であるため、
「点滴をしても、赤血球・ヘモグロビン・ヘマトリックの値は、下がらない。」という
「帰無仮説」は、「棄却（否定）」される。
従って、
（03）（16）により、
（17）
（ⅱ）「点滴（輸液）」を行うと、「血液が希釈され」、「血液が希釈され」ると、「赤血球・Ｈｂ・Ｈｔの値が低下」する。
という「命題」は、「患者（The patient）」に対しても、「正しい」。
然るに、
（18）

従って、
（18）により、
（19）
①『脱水』であれば（「点滴」をすれば「（赤血球 等の）数値」が下がる）。
然るに、
（20）
１　　　（１）　Ｐ→（Ｑ→　Ｒ）　Ａ
　２　　（２）　　　　Ｑ＆～Ｒ　　Ａ
　　３　（３）　　　　Ｑ→　Ｒ　　Ａ
　２　　（４）　　　　Ｑ　　　　　２＆Ｅ
　２３　（５）　　　　　　　Ｒ　　３４ＭＰＰ
　２　　（６）　　　　　　～Ｒ　　２＆Ｅ
　２３　（７）　　　　Ｒ＆～Ｒ　　５６＆Ｉ
　２　　（８）　　～（Ｑ→　Ｒ）　３７ＲＡＡ
１２　　（９）～Ｐ　　　　　　　　１８ＭＴＴ
１　　　（ア）（Ｑ＆～Ｒ）→～Ｐ　２９ＣＰ
　　　イ（イ）　　　　　　　　Ｐ　Ａ
　　　イ（ウ）　　　　　　～～Ｐ　イＤＮ
１　　イ（エ）　～（Ｑ＆～Ｒ）　　アウＭＴＴ
１　　イ（オ）　　～Ｑ∨　Ｒ　　　エ、ド・モルガンの法則
１　　イ（カ）　　　Ｑ→　Ｒ　　　オ含意の定義
１　　　（キ）Ｐ→（Ｑ→　Ｒ）　　イカＣＰ
従って、
（19）（20）により、
（21）
①　Ｐ→（Ｑ→Ｒ）
②（Ｑ＆～Ｒ）→～Ｐ
に於いて、
Ｐ＝脱水である。
Ｑ＝点滴をする。
Ｒ＝数値が下がる。
という「代入」を行うと、
①『脱水』であれば（「点滴」をすれば「（赤血球 等の）数値」が下がる）。
②（「点滴」をしても「（赤血球 等の）数値」が下がらない）場合は『脱水』ではない。
に於いて、
①＝② は、「（逆ではなく）対偶」です。
従って、
（21）により、
（22）
①『脱水』であれば（「点滴」をすれば「（赤血球 等の）数値」が下がる）。
②（「点滴」をしても「（赤血球 等の）数値」が下がらない）場合は『脱水』ではない。
③（「点滴」をすれば「（赤血球 等の）数値」が下がる）ならば『脱水』。
に於いて、
①＝② は、「対偶」であって、
①≠③ は、「逆」である。
然るに、
（23）
「ことわざ」として、誰もが知っている通り、
「逆」は必ずしも真ではない（the reverse is not always true）。
従って、
（03）（18）（22）（23）により、
（24）
①『脱水』であっても、『脱水』でなくとも、いずれにせよ「点滴」をすれば、「血液の希釈」が起こり「（赤血球 等の）数値は下がる」が、
②「点滴」による「血液の希釈」があっても、「数値は下がらない」のであれば、『脱水』ではない。
然るに、
（25）

従って、
（25）により、
（26）

という風に、
「赤血球」に関しては、　　「上がって、下がっている（元に戻っている）」が、
「クレアチニン」の場合は、「急上昇」の「後」で、「更に、上がっている」。
従って、
（24）（25）（26）により、
（27）
②「点滴」による「血液の希釈」があっても、「数値は下がらない」のであれば、『脱水』ではない。
が故に、

という「（点滴を再開しても更に上昇する）クレアチニンの上昇（Ｃｒｅ）」の「原因」は、『脱水』では、有り得ない。
然るに、
（28）

　　　　　　　　　　　　　（それぞれの、「１月１８日の値」を、「１.０」として、「グラフ」にしている。）
従って、
（18）（27）（28）により、
（29）
「Ｃｒｅ（腎臓の指標）」に加えて、
「ＢＵＮ（腎臓の指標）」を見れば、分かるように、

という「診断」は、明らかに、『誤診』である。
然るに、
（30）
患者に対して医師が薬を投与したときに、蕁麻疹が生じる等の症状が出たときには、薬の副作用の疑いもあります。このとき、同じ薬を投与し続ければ、さらに重い副作用が発生して深刻な影響が生じることを予見し、薬の投与を中断したり、薬の種類を変更したりして、深刻な影響が生じるという結果を回避できる場合があります。このような予見可能性と結果回避可能性は、注意義務違反（過失）の前提として必要とされるものです（医学博士 弁護士 金﨑浩之）。
従って、
（30）により、
（31）
たとえ、『誤診』によって、「患者が死亡した」場合であっても、『誤診』自体は、「罪」にはならない。
（32）
「白巨塔（ＴＶドラマ）」の場合、
『癌性リンパ管症を見落とした』ことは、『誤診』であったが、財前五郎は、そのこと自体では「有罪」にはならず、
たとえ「（手術の）承諾書」が書かれていたとしても、「治療方法」を、「患者自身の意思」に委ねなかったことを「理由」に、「二審」に於いて、「有罪」になっている。
ｃｆ.
財前五郎　　：「承諾書」というものは「承諾」したら書くものです。
佐々木よし江：助かりたかったら「手術しかない」と言われたら、「承諾書」を書くしかないじゃないですか！！
然るに、
（33）
２０１９年０１月２７日１１時４８分前後の、ナースステーションに於いて、
Ｓ医師は、私に対して、ハッキリと、「今、投与をしている薬」は、

 

　　　　　　　　　　　　　　　　　　　　（２０１２年０７月０５日、Ｋ医師）
でいう所のその「フェブリク（ によるアレルギーＳ/Ｏ→中止）」であることを、告げるべきであった。
然るに、
（34）
２０１９年０２月０３日（葬儀の翌日）の「ｇｏｏブログ」を見ると、

となっている。
従って、
（33）（34）により、
（35）
鈴木医師は、
「前の薬」＝「１番目の薬」ではなく、
「別の薬」＝「２番目の薬」＝「フェブリク（ によるアレルギーＳ/Ｏ→中止）」を、もう一度、
「０１月０５日」から「投与」している。
ということを、「私に分かるよう」には、「説明していない」。

（1226）「逆」だけでなく「裏」も必ずしも「真」ではない。

（01）
① 法律を知らないと不幸になる。
② 不幸にならないならば法律を知っている。
③ 不幸になるならば法律を知らない。
④ 法律を知っていれば不幸にならない。
⑤ 法律を知ってるのに不幸になる。
に於いて、
① は「順」　であって、
② は「対偶」であって、
③ は「逆」　であって、
④ は「裏」　であるが、
⑤ は、特に「名前」はない。
然るに、
（02）
① 法律を知らないと不幸になる（順）。
② 不幸にならないならば法律を知っている（対偶）。
③ 不幸になるならば法律を知らない（逆）。
④ 法律を知っていれば不幸にならない（裏）。
に於いて、
①＝② は「対偶の関係」であって、
③＝④ も「対偶の関係」である。
然るに、
（03）
「逆は、必ずしも真ではない。」
という「言い方」があるように、
① 法律を知らないと不幸になる（順）。
③ 不幸になるならば法律を知らない（逆）。
に於いて、
①＝③ ではない。
従って、
（02）（03）により、
（04）
① 法律を知らないと不幸になる（順）。
④ 法律を知っていれば不幸にならない（裏）。
に於いて、
①＝④ ではなく、その「意味」で、
「逆は、必ずしも真ではなく、」
「裏も、必ずしも真ではない。」
然るに、
（05）
① 法律を知らないと不幸になる（逆）。
④ 法律を知っていれば不幸にならない（裏）。
⑤ 法律を知ってるくせに不幸になる。
に於いて、
④と⑤ は「矛盾」する。
従って、
（04）（05）により、
（06）
① 法律を知らないと不幸になる（逆）。
④ 法律を知っていれば不幸にならない（裏）。
⑤ 法律を知ってるくせに不幸になる。
に於いて、「実際」には、
①＝④ でない、にも拘わらず、
①＝④ であると「誤解」すると、
①と⑤ は「矛盾」するという、「勘違い」が生じることになる。
然るに、
（07）
瀧田早苗、二七才、東京大学法学部卒、―中略―つまり、極めて優秀なエリートだということだ。―中略―、
「正義の定義によりますね。先生は、ずっと法律を知らないと不幸になると、おっしゃっています。
　まったく同感です。でも、多くの弁護士は、法律を知っているくせに、依頼者を幸福にできていません。」
（真山仁 作、レインメーカー）
従って、
（07）により、
（08）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検、美人）は、
① 法律を知らないと不幸になる（逆）。
⑤ 法律を知ってるくせに不幸になる。
に於いて、
①と⑤ は「矛盾」するという風に、言っている。
従って、
（06）（07）（08）により、
（09）
① 法律を知らないと不幸になる（逆）。
④ 法律を知っていれば不幸にならない（裏）。
⑤ 法律を知ってるくせに不幸になる。
に於いて、「実際」には、
①＝④ ではない、にも拘わらず、
①＝④ であると「誤解」することによって、
①と⑤ は「矛盾」するという風に、述べている。
然るに、
（10）
④ 法律を知っていれば不幸にならない（裏）。
というのであれば、
④ 法律家は、誰もが幸福であるが、実際には、
④ 幸福ではない法律家は、いないはずがない。
従って、
（07）～（10）により、
（11）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検、美人）は、「結果」として、
① 法律を知らないと不幸になる（逆）。
④ 法律を知っていれば不幸にならない（裏）。
⑤ 法律を知ってるくせに不幸になる。
に於いて、
①＝④ ではない、にも拘わらず、
①＝④ であると「誤解」することによって、
①と⑤ は「矛盾」するという風に、述べているが、
④ 法律を知っていれば不幸にならない（裏）。
ということは、「真（本当）」ではない。
従って、
（11）により、
（12）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検、美人）は、
少なくとも、「論理（学）的」であるとは、言えない。
然るに、
（13）
同じく「論理」を展開させるといっても、法律家の論証と数学や論理学の証明問題を解くのとは、同じではないでしょう。では、どこが違うのでしょうか。憲法学の場合はどうでしょうか。
目が眩むほど大きな問いですが、具体例を手がかりとしながら探ってみようと思います（法学の論理、憲法学の論理）。
然るに、
（14）
「法律家の論証と数学や論理学の証明問題を解くのとは、同じではないでしょう。」というのであれば、
「法律家のいう論理」とは、「フレーゲや、ラッセルや、ウィトゲンシュタインタインがいう論理（古典論理）」とは「同じ」ではないし、だとすれば、
「そのような論理（法律家のいう論理）」は、所謂、「論理」ではない。

（1225）「フェルマーの最終定理」と「対偶（の関係性）」（Ⅱ）。

（01）
フライさんは手からチョークを払うため、両手をパンパンと叩きながら続けます。
「さて、よく見ると、この方程式は楕円曲線の形をしていることがおかかりでしょうか？
ということは、フェルマーの最終定理がなりたたないとすればこのよう楕円曲線が存在してしまうことを意味しますね」
「うわっ、たしかに！」
僕の横で聞いていたフライさんの学友が大きな声を上げました。
「で、この楕円曲線はあまりにも特異であるために、モジュラー形式にはならないんです」
「・・・ってことは・・・・・」
「そうです、あとはお察しの通リです」
（ざわざわざわ・・・）
「つまり、対偶の関係性によって、谷山＝志村予想が正しければフェルマーの最終定理も正しい・・・？」
（［小説］フェルマーの最終定理、日沖桜皮、2010年、１３８頁）
然るに、
（02）
数学において、谷山・志村予想（たにやましむらよそう、Taniyama–Shimura conjecture）は、「すべての有理数体上に定義された楕円曲線はモジュラーである」という主張であり、
アンドリュー・ワイルズとその弟子クリストフ・ブロイル、ブライアン・コンラッド、フレッド・ダイアモンド、リチャード・テイラーらによって証明された。
（ウィキペディア）
従って、
（01）（02）により、
（03）
（ⅰ）『「フェルマーの最終定理」が「マチガイ」であるならば、ある「モジュラーではない、楕円曲線」が存在する。』然るに、
（ⅱ）『「谷山＝志村予想」が「正しい」とすれば、「モジュラーではない、いかなる楕円曲線」も存在しない。』　　　従って、
（ⅲ）『「フェルマーの最終定理」が「マチガイ」であって、「谷山＝志村予想」が「正しい」といふことはない。』　　従って、
（ⅳ）『「谷山＝志村予想」が「正しく」て、「フェルマーの最終定理」が「マチガイ」であるといふことはない。』　　従って、
（ⅴ）『「谷山＝志村予想」が「正しい」ならば「フェルマーの最終定理（予想）」も「正しい」。』
然るに、
（04）
（ⅲ）
１（１）～（～Ｆ＆谷）　Ａ
１（２）～（谷＆～Ｆ）　１交換法則
（ⅳ）
１（１）～（谷＆～Ｆ）　Ａ
１（２）～（～Ｆ＆谷）　１交換法則
然るに、
（05）
（ⅳ）
１　　（１）～（谷＆～Ｆ）　　Ａ
　２　（２）　　谷　　　　　　Ａ
　　３（３）　　　　～Ｆ　　　Ａ
　２３（４）　　谷＆～Ｆ　　　２３＆Ｉ
１２３（５）～（谷＆～Ｆ）＆
　　　　　　　（谷＆～Ｆ）　　１４＆Ｉ
１２　（６）　　　～～Ｆ　　　３５ＲＡＡ
１２　（７）　　　　　Ｆ　　　６ＤＮ
１　　（８）　　谷→　Ｆ　　　２７ＣＰ
（ⅴ）
１　　（１）　　谷→　Ｆ　　　Ａ
　２　（２）　　谷＆～Ｆ　　　Ａ
　２　（３）　　谷　　　　　　２＆Ｅ
１２　（４）　　　　　Ｆ　　　１３ＭＰＰ
　２　（５）　　　　～Ｆ　　　２＆Ｅ
１２　（６）　　Ｆ＆～Ｆ　　　４５＆Ｉ
１　　（７）～（谷＆～Ｆ）　　２６ＲＡＡ
従って、
（03）（04）（05）により、
（06）
（ⅰ）『「フェルマーの最終定理」が「マチガイ」であるならば、ある「モジュラーではない、楕円曲線」が存在する。』然るに、
（ⅱ）『「谷山＝志村予想」が「正しい」とすれば、「モジュラーではない、いかなる楕円曲線」も存在しない。』　　　従って、
（ⅲ）『「フェルマーの最終定理」が「マチガイ」であって、「谷山＝志村予想」が「正しい」といふことはない。』　　従って、
（ⅳ）『「谷山＝志村予想」が「正しく」て、「フェルマーの最終定理」が「マチガイ」であるといふことはない。』　　従って、
（ⅴ）『「谷山＝志村予想」が「正しい」ならば「フェルマーの最終定理（予想）」も「正しい」。』
といふ「推論」は、「命題論理」として「正しい」。

（1224）「フェルマーの最終定理」と「対偶（の関係性）」。

（01）
フライさんは手からチョークを払うため、両手をパンパンと叩きながら続けます。
「さて、よく見ると、この方程式は楕円曲線の形をしていることがおかかりでしょうか？
ということは、フェルマーの最終定理がなりたたないとすればこのよう楕円曲線が存在してしまうことを意味しますね」
「うわっ、たしかに！」
僕の横で聞いていたフライさんの学友が大きな声を上げました。
「で、この楕円曲線はあまりにも特異であるために、モジュラー形式にはならないんです」
「・・・ってことは・・・・・」
「そうです、あとはお察しの通リです」
（ざわざわざわ・・・）
「つまり、対偶の関係性によって、谷山＝志村予想が正しければフェルマーの最終定理も正しい・・・？」
（［小説］フェルマーの最終定理、日沖桜皮、2010年、１３８頁）
然るに、
（02）
数学において、谷山・志村予想（たにやましむらよそう、Taniyama–Shimura conjecture）は、「すべての有理数体上に定義された楕円曲線はモジュラーである」という主張であり、
アンドリュー・ワイルズとその弟子クリストフ・ブロイル、ブライアン・コンラッド、フレッド・ダイアモンド、リチャード・テイラーらによって証明された。
（ウィキペディア）
従って、
（01）（02）により、
（03）
（ⅰ）『「フェルマーの最終定理（予想）」が「マチガイ」であるならば、ある「モジュラーではない、楕円曲線」が存在する。』然るに、
（ⅱ）『「谷山＝志村予想」が「正しい」とすれば、「モジュラーではない、いかなる楕円曲線」も存在しない。』従って、
（ⅲ）『「フェルマーの最終定理（予想）」が「マチガイ」であるならば、「谷山＝志村予想」も「マチガイ」である。』
然るに、
（04）
～Ｆ＝「フェルマーの最終定理（予想）」は「偽（マチガイ）」である。
～Ｔ＝「谷山＝志村予想」は「偽（マチガイ）」である。

とする。
従って、
（03）（04）により、
（05）
（ⅰ）『「フェルマーの最終定理（予想）」が「マチガイ」であるならば、ある「モジュラーではない、楕円曲線」が存在する。』然るに、
（ⅱ）『「谷山＝志村予想」が「正しい」とすれば、「モジュラーではない、いかなる楕円曲線」も存在しない。』従って、
（ⅲ）『～Ｆ→～Ｔ』である。
然るに、
（06）
（ⅰ）
１　　（１）　～Ｆ→～Ｔ　Ａ
　２　（２）　　　　　Ｔ　Ａ
　　３（３）　～Ｆ　　　　Ａ
１　３（４）　　　　～Ｔ　１３ＭＰＰ
１２３（５）　　Ｔ＆～Ｔ　２４＆Ｉ
１２　（６）～～Ｆ　　　　３５ＲＡＡ
１２　（７）　　Ｆ　　　　６ＤＮ
１　　（８）　　Ｔ→Ｆ　　２７ＣＰ
（ⅱ）
１　　（１）　Ｔ→　Ｆ　Ａ
　２　（２）　　　～Ｆ　Ａ
　　３（３）　Ｔ　　　　Ａ
１　３（４）　　　　Ｆ　１３ＭＰＰ
１２３（５）～Ｆ＆　Ｆ　２４＆Ｉ
１２　（６）～Ｔ　　　　３５ＲＡＡ
１　　（７）～Ｆ→～Ｔ　２６ＣＰ
従って、
（06）により、
（07）
① ～Ｆ→～Ｔ
② 　Ｔ→　Ｆ
に於いて、
①＝② は「対偶」である。
従って、
（05）（06）（07）により、
（08）
（ⅰ）『「フェルマーの最終定理（予想）」が「マチガイ」であるならば、ある「モジュラーではない、楕円曲線」が存在する。』然るに、
（ⅱ）『「谷山＝志村予想」が「正しい」とすれば、「モジュラーではない、いかなる楕円曲線」も存在しない。』従って、
（ⅲ）『Ｔ→Ｆ』である。
従って、
（04）（08）により、
（09）
（ⅰ）『「フェルマーの最終定理（予想）」が「マチガイ」であるならば、ある「モジュラーではない、楕円曲線」が存在する。』然るに、
（ⅱ）『「谷山＝志村予想」が「正しい」とすれば、「モジュラーではない、いかなる楕円曲線」も存在しない。』従って、
（ⅲ）『「谷山＝志村予想」が「正しい」とすれば、「フェルマーの最終定理（予想）」も「正しい」。』
従って、
（01）～（09）により、
（10）
「つまり、対偶の関係性によって、谷山＝志村予想が正しければフェルマーの最終定理も正しい・・・！」
然るに、
（11）
① 大和なでしこ（日本人の女性）であるならば、女性である。
② 女性でないならば、大和なでしこ（日本人の女性）ではない。
に於いて、
①＝② であることは、
③「大和なでしこ（日本人の女性）」の「集合」が、
④「女性の集合」の「真部分集合」である、ということからすれば、「当然」である。
然るに、
（12）
①「フェルマーの最終定理」は「命題」であって、「集合」ではなく、
②「谷山＝志村予想」も「命題」であって、「集合」ではない。
従って、
（11）（12）により、
（13）
「対偶」は、
③「大和なでしこ」の「集合」と、
④「女性の集合」　の「集合」のように、「集合」で「理解」するのが、「一番簡単」であるが、
①「フェルマーの最終定理」は「集合」ではなく、「命題」であって、
②「谷山＝志村予想」も「集合」ではなく、「命題」である。

（1223）「法律家にも論理学は必要である（？）」：「順・対偶・逆・裏」について。

（01）
①「大和なでしこ」であるならば「女性」である（順）。
②「女性」でないならば「大和なでしこ」ではない（対偶）。
③「女性」であるならば「大和なでしこ」である（逆）。
④「大和なでしこ」でないならば「女性」でない（裏）。
ということは、
①「日本人＆女性」であるならば「女性」である（順）。
②「女性」でないならば「日本人＆女性」ではない（対偶）。
③「女性」であるならば「日本人＆女性」である（逆）。
④「日本人＆女性」でないならば「女性」ではない（裏）。
ということである。
従って、
（01）により、
（02）
①「大和なでしこ」であるならば「女性」である（順）。
②「女性」でないならば「大和なでしこ」ではない（対偶）。
に於いて、明らかに、
① は「真（本当）」であって、
② も「真（本当）」である。
然るに、
（03）
③「外国人＆女性」であれば、「女性」であるが、
③「外国人＆女性」であれば、「日本人女性（大和なでしこ）」ではない。
従って、
（01）（03）により、
（04）
③「女性」であるならば「大和なでしこ」である（逆）。
という「命題」は、「真」であるとは、限らない。
然るに、
（05）
④「日本人＆女性」でない。
ということは、
④「外国人＆女性」である。
④「日本人＆男性」である。
④「外国人＆男性」である。
という「３通り」の、「どれか１つ」である。
然るに、
（06）
④「外国人＆女性」であるならば、　　　「女性」であるため、
④「日本人＆女性」でないからと言って、「女性」でないとは、言えない。
従って、
（01）（06）により、
（07）
④「外国人＆女性」であるならば、　　　「女性」であるため、
④「大和なでしこ」でないからと言って、「女性」でないとは、言えない。
従って、
（02）（04）（07）により、
（08）
①「大和なでしこ」であるならば「女性」である（順）。
②「女性」でないならば「大和なでしこ」ではない（対偶）。
③「女性」であるならば「大和なでしこ」である（逆）。
④「大和なでしこ」でないならば「女性」でない（裏）。
に於いて。
① は「真（本当）」であって、
② も「真（本当）」であるものの、その一方で、
③ は「偽（ウソ）」であって、
④ も「偽（ウソ）」である。
従って、
（08）により、
（09）
Ｐ＝大和なでしこである。
Ｑ＝女性である。
として、
① 　Ｐ→　Ｑ（順）
② ～Ｑ→～Ｐ（対偶）
③ 　Ｑ→　Ｐ（逆）
④ ～Ｐ→～Ｑ（裏）
に於いて、
①＝② であるが、
①＝③ ではないし、
①＝④ でもない。
従って、
（09）により、
（10）
Ｐ＝任意の命題。
Ｑ＝任意の命題。
として、
① 　Ｐ→　Ｑ（順）
② ～Ｑ→～Ｐ（対偶）
③ 　Ｑ→　Ｐ（逆）
④ ～Ｐ→～Ｑ（裏）
に於いて、
①＝② であるが、
①＝③ ではないし、
①＝④ でもない。
従って、
（10）により、
（11）
Ｐ＝～Ｐ
という「代入」を行ふと、
① 　～Ｐ→　　Ｑ（順）
②　 ～Ｑ→～～Ｐ（対偶）
③ 　  Ｑ→　～Ｐ（逆）
④ ～～Ｐ→　～Ｑ（裏）
に於いて、
①＝② であるが、
①＝③ ではないし、
①＝④ でもない。
従って、
（11）により、
（12）
「二重否定」により、
① ～Ｐ→　Ｑ（順）
② ～Ｑ→　Ｐ（対偶）
③   Ｑ→～Ｐ（逆）
④ 　Ｐ→～Ｑ（裏）
に於いて、
①＝② であるが、
①＝③ ではないし、
①＝④ でもない。
然るに、
（12）により、
（13）
① ～Ｐ→　Ｑ（順）
② 　Ｐ→　Ｑ（？）
③ 　Ｐ→～Ｑ（裏）
に於いて、
①と②の「関係」に、「名前」は無く、
①と③の「関係」は、「順と裏」である。
然るに、
（14）
１　　（１）Ｐ→　Ｑ　Ａ
　２　（２）Ｐ→～Ｑ　Ａ
　　３（３）Ｐ　　　　Ａ
１　３（４）　　　Ｑ　１３ＭＰＰ
　２３（５）　　～Ｑ　２３ＭＰＰ
１２３（６）Ｑ＆～Ｑ　４５＆Ｉ
従って、
（13）（14）により、
（15）
① ～Ｐ→　Ｑ（順）
② 　Ｐ→　Ｑ（？）
③ 　Ｐ→～Ｑ（裏）
に於いて、
②と③は、「矛盾」する。
従って、
（10）（15）により、
（16）
① ～Ｐ→　Ｑ（順）
② 　Ｐ→　Ｑ（？）
③ 　Ｐ→～Ｑ（裏）
に於いて、
①＝③ であると、「勘違い（誤解）」をすると、
①と② は「矛盾」する。
然るに、
（17）
Ｐ＝法律を知っている。
Ｑ＝不幸になる。
とすると、
① 法律を知らないと不幸になる（順）。
② 法律を知っているくせに不幸になる（？）。
③ 法律を知ってさえいれば不幸にならない（裏）。
という「命題」は、
① ～Ｐ→　Ｑ（順）
② 　Ｐ→　Ｑ（？）
③ 　Ｐ→～Ｑ（裏）
という風に、書くこと出来る。
従って、
（16）（17）により、
（18）
① 法律を知らないと不幸になる（順）。
② 法律を知っているくせに不幸になる（？）。
③ 法律を知ってさえいれば不幸にならない（裏）。
に於いて、
①＝③ であると、「勘違い（誤解）」をすると、
①と② は「矛盾」する。
然るに、
（19）
瀧田早苗、二七才、東京大学法学部卒、―中略―つまり、極めて優秀なエリートだということだ。―中略―、
「正義の定義によりますね。先生は、ずっと法律を知らないと不幸になると、おっしゃっています。
　まったく同感です。でも、多くの弁護士は、法律を知っているくせに、依頼者を幸福にできていません。」
（真山仁 作、レインメーカー）
然るに、
（19）により、
（20）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検、美人）は、
① 法律を知らないと不幸になる（順）。
② 法律を知っているくせに不幸になる（？）。
に於いて、
①と② は「矛盾」すると、思っている。
従って、
（18）（19）（20）により、
（21）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検、美人）は、
① 法律を知らないと不幸になる（順）。
③ 法律を知ってさえいれば不幸にならない（裏）。
に於いて、
①＝③ であると、「勘違い（誤解）」をしている。
然るに、
（22）
瀧田早苗（二七才、東京大学法学部卒、ヤメ検、美人）は、「論理学の初歩」である、「順と裏」の「区別」が付かないし、
③ 法律を知ってさえいれば不幸にならない（裏）。
という「命題」は、「真（本当）」であるとは、言えない。
従って、
（22）により、
（23）
小説の中の、瀧田早苗（二七才、東京大学法学部卒、ヤメ検、美人）を、
極めて優秀なエリートだとすることは、出来ない。
然るに、
（24）
とある法学徒の社会探訪：
法律学というのは、時に、同じ出発点である、例えば条文やより高次の法理を共有しながら、結論を異にすることがあります（例えば、拙稿「表立ってはいえない犯罪論その２」で挙げた事例も、結論を異にする発想は、十分にあり得ます）。そうであれば、法律学は「論理的な学」ではないということになりそうです（そして、おそらく、この現実に気づいた法律学の初学者は一気に法律学に対する興味をなくしているのではないかとすら疑われます）。
とのことである。
令和０４年０８月０１日、毛利太。