(01)
(ⅰ)
1 (1) ∀x(象x→ 動物x) A
1 (2) 象a→ 動物a 1UE
3(3) ~動物a A
13(4) ~象a 23MTT
1 (5) ~動物a→~象a 34CP
1 (6)∀x(~動物x→~象x) 5UI
(ⅱ)
1 (1)∀x(~動物x→~象x) A
1 (2) ~動物a→~象a 1UE
3(3) 象a A
3(4) ~~象a 3DN
13(5) ~~動物a 24MTT
13(6) 動物a 5DN
1 (7) 象a→ 動物a 36CP
1 (8) ∀x(象x→ 動物x) 7UI
従って、
(01)により、
(02)
① ∀x( 象x→ 動物x)
② ∀x(~動物x→~象x)
に於いて、すなはち、
① すべてのxについて(xが象であるならば、xは動物である)。
② すべてのxについて(xが象でないならば、xは動物でない)。
に於いて、すなはち、
①「象の集合」は、「動物の集合」の「部分集合」である。
②「動物の集合」の「補集合」は「象の集合」の「部分集合」ではない。
に於いて、すなはち、
①「象であるものは動物であるものである。」
②「動物でないものは象でないものである。」
に於いて、
①=② である。
然るに、
(03)
①「象であるものは動物であるものである。」
②「動物でないものは象でないものである。」
に於いて、
① は、② の「対偶(contraposition)」であり、
② も、① の「対偶(contraposition)」である。
従って、
(04)
「対偶(の真偽)」は、「(互いに)等しい」。
然るに、
(05)
「Aである」といふ「事態の集合」
「Bである」といふ「事態の集合」
を「想定」しても、
①「事態A」であるならば「事態B」である。
②「事態B」でないならば「事態A」でない。
に於いて、
①=② は「対偶(contraposition)」である。
cf.
事実は諸「事態」から、そして「事態」は諸対象から構成されている(ヴィトゲンシュタイン)。
従って、
(01)~(05)により、
(06)
①「象であるものは動物であるものである。」
②「動物でないものは象でないものである。」
といふ「命題」に於ける、
①=② を含めて、一般に、
① Aであるならば、Bである。
② Bでないならば、Aでない。
といふ「事態」に於いて、
①=② は「対偶(contraposition)」である。
因みに、
(07)
(ⅰ)
1 (1) ∀x(象x→ 動物x) A
2 (2) ∃x(象x&~動物x) A
1 (3) 象a→ 動物a 1UE
4(4) 象a&~動物a A
4(5) 象a 4&E
1 4(6) 動物a 35MPP
4(7) ~動物a 4&E
1 4(8) 動物a&~動物a 67&I
4(9)~∀x(象x→ 動物x) 18RAA
2 (ア)~∀x(象x→ 動物x) 249EE
12 (イ) ∀x(象x→ 動物x)&
~∀x(象x→ 動物x) 1ア&I
1 (ウ)~∃x(象x&~動物x) 2イRAA
(ⅱ)
1 (1)~∃x(象x&~動物x) A
1 (2)∀x~(象x&~動物x) 1量化子の関係
1 (3) ~(象a&~動物a) 2UE
4 (4) 象a A
5(5) ~動物a A
45(6) 象a&~動物a 45&I
145(7) ~(象a&~動物a)&
(象a&~動物a) 36&I
14 (8) ~~動物a 57RAA
14 (9) 動物a 8DN
1 (ア) 象a→ 動物a 9CP
1 (イ) ∀x(象x→ 動物x) アUI
従って、
(07)により、
(08)
① ∀x(象x→ 動物x)
② ~∃x(象x&~動物x)
に於いて、すなはち、
① すべてのxについて(xが象であるならば、xは動物である)。
②(象であって、動物でないx)は存在しない。
に於いて、
①=② は「対偶(contraposition)」である。
(01)
(ⅰ)
1 (1) P→(Q→ R) A
2 (2) Q&~R A
3(3) Q→ R A
2 (4) Q 2&E
23(5) R 34MPP
2 (6) ~R 45&I
23(7) R&~R 56&I
2 (8) ~(Q→ R) 37RAA
12 (9)~P 18MTT
1 (ア)(Q&~R)→~P 29CP
(ⅱ)
1 (1) (Q&~R)→~P A
2 (2) P A
2 (3) ~~P 2DN
12 (4) ~(Q&~R) 13MTT
5 (5) Q A
6(6) ~R A
56(7) Q&~R 56&I
1256(8) ~(Q&~R)&
(Q&~R) 47&I
125 (9) ~~R 68RAA
125 (ア) R 9DN
12 (イ) Q→ R 5アCP
1 (ウ)P→(Q→ R) 2イCP
従って、
(01)により、
(02)
① P→(Q→R)
②(Q&~R)→~P
に於いて、
①=② は「対偶(contraposition)」である。
然るに、
(03)
① P→(Q→ R)
②(Q&~R)→~P
に於いて、
P=脱水である。
Q=点滴をする。
R=数値は下降する。
といふ「代入」を行ふと、
①「脱水」であるならば、(点滴をすれば、数値は下降する)。
②(点滴をしても、数値が下降しない)ならば、「脱水」ではない。
に於いて、
①=② は「対偶(contraposition)」である。
然るに、
(04)
S先生曰く、
(ⅰ)「1月25日の血液検査」で、
(ⅱ)「脱水による血液濃縮」による、
(ⅲ)「赤血球数・クレアチニン」等の「数値」が「上昇」が見られたため、
(ⅳ)「1月25日」より、「輸液(点滴)」を再開した。
cf.
従って、
(03)(04)により、
(05)
S先生は、「対偶」で言ふと、
① 「脱水」なので、(点滴をすれば、数値は下降する)。⇔
②(点滴をしても、数値が下降しない)ならば、「脱水」ではない。
といふ『診断』を下してゐる。
然るに、
(06)
(07) 従って、
(06)(07)により、
(08)
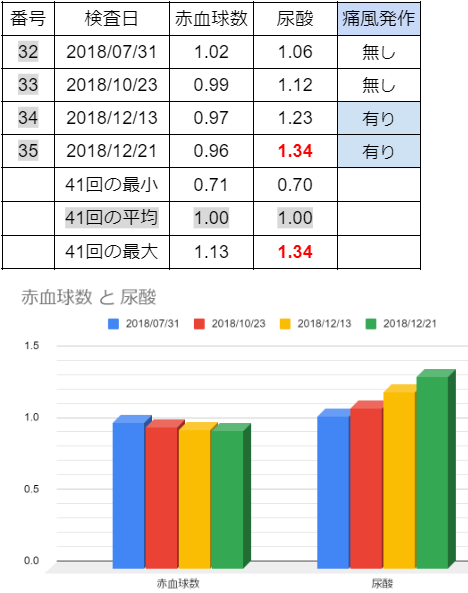
「07月31日(点滴無し)」の「赤血球」
「10月23日(点滴無し)」の「赤血球」
「12月13日(点滴無し)」の「赤血球」
「12月21日(点滴無し)」の「赤血球」
「12月26日(点滴有り)」の「赤血球」
「01月04日(点滴有り)」の「赤血球」
「01月11日(点滴有り)」の「赤血球」
「01月18日(点滴有り)」の「赤血球」
「01月25日(点滴無し)」の「赤血球」
「01月29日(点滴有り)」の「赤血球」
の『グラフ』は、
といふ『具合』に、
「07月31日(点滴無し)」の「赤血球」は「普通」であり、
「10月23日(点滴無し)」の「赤血球」も「普通」であり、
「12月13日(点滴無し)」の「赤血球」も「普通」であり、
「12月21日(点滴無し)」の「赤血球」も「普通」であるが、
「12月26日(点滴有り)」の「赤血球」は「血液が希釈」され、その分、「低い」。
「01月04日(点滴有り)」の「赤血球」は「血液が希釈」され、その分、「低い」。
「01月11日(点滴有り)」の「赤血球」は「血液が希釈」され、その分、「低い」。
「01月18日(点滴有り)」の「赤血球」は「血液が希釈」され、その分、「低い」。
「01月25日(点滴無し)」の「赤血球」は「普通」であり、
「01月29日(点滴有り)」の「赤血球」は「血液が希釈」され、その分、「低い」。
然るに、
(06)(07)により、
(09)
「07月31日(点滴無し)」の「クレアチニン」
「10月23日(点滴無し)」の「クレアチニン」
「12月13日(点滴無し)」の「クレアチニン」
「12月21日(点滴無し)」の「クレアチニン」
「12月26日(点滴有り)」の「クレアチニン」
「01月04日(点滴有り)」の「クレアチニン」
「01月11日(点滴有り)」の「クレアチニン」
「01月18日(点滴有り)」の「クレアチニン」
「01月25日(点滴無し)」の「クレアチニン」
「01月29日(点滴有り)」の「クレアチニン」
の『グラフ』は、
といふ『具合』に、
「07月31日(点滴無し)」の「クレアチニン」は「普通」であり、
「10月23日(点滴無し)」の「クレアチニン」は「普通」であるが、
「12月13日(点滴無し)」の「クレアチニン」は「異常に高く」、
「12月21日(点滴無し)」の「クレアチニン」も「異常に高く」、
「12月26日(点滴有り)」の「クレアチニン」は「血液が希釈」され、その分、「低い」。
「01月04日(点滴有り)」の「クレアチニン」は「血液が希釈」され、その分、「低い」。
「01月11日(点滴有り)」の「クレアチニン」は「血液が希釈」され、その分、「低い」。
「01月18日(点滴有り)」の「クレアチニン」は「血液が希釈」され、その分、「低い」。
「01月25日(点滴無し)」の「クレアチニン」は「極端に高く」、
「01月29日(点滴有り)」の「クレアチニン」は「血液が希釈」され、その分、「低い」はずであるにも、拘わらず、
「更に、極端に高い」。
従って、
(06)(09)により、
(10)
「01月18日(点滴有り)」の「クレアチニン」は「血液が希釈」され、その分、「低い」。
「01月25日(点滴無し)」の「クレアチニン」は「極端に高く」、
「01月29日(点滴有り)」の「クレアチニン」は「血液が希釈」され、その分、「低い」はずであるにも、拘わらず、
「更に、極端に高い」。
といふ「事実」により、S先生による、
① 脱水なので、(点滴をすれば、数値は下降する)。
といふ『診断』は、『誤診』であると、「言はざるを得ない」。
(11)
「私の父」は、「退院した当日」に「再入院」をして、「その日の内に死亡した」のであるが、
「01月29日(点滴有り)」の「クレアチニン」は「血液が希釈」され、その分、「低い」はずであるにも、拘わらず、
「更に、極端に高い」。
といふ「(再入院の際)のデータ」が無かったとしたら、
S先生の『誤診』を「証明」することは、「叶はなかった」。
(12)
「41回の、検査結果」は、
「41回の、各々の回の、赤血球を、1.00とした場合」は、 従って、
(12)(13)により、
(14)
「私の父」は、遅くとも、「1月25日」に、
「脱水」ではなく、「急性腎不全」を「発症」し、「4日後に、死亡してゐる」が、
「1月4日」から「投与」された「フェブリク」は、「同じ病院の前医」によって、『禁忌』とされてゐる。
cf. (15)
S先生には、中央区の弁護士(は病院側)を介して、3カ月前に、「長文の質問」を「送付」しているが、「(3回ほど催促しているにも拘わらず、)未だに、回答」が無い。
(16)
「仮説検定の数値(約0.13%)」から言っても、
S医師が、私に「反論」することは、「ほとんど、不可能」であると、考へます。
然るに、
(17)
「私が争点にしたい」のは、『数学や論理学の定理』ではないため、「原理的に証明」が「不可能」な、
「フェブリクの副作用で、父が死亡した」といふことではなく、「生成AIが要約」した、 といふ『事柄(説明義務違反)』です。
(01)
P= 脱水である。
Q=血液濃縮である。
R=赤血球数が上昇する。
S= 尿酸値が上昇する。
とする。
然るに、
(02)
1 (1) P→Q A
2 (2) Q→(R&S) A
3(3) ~R&S A
3(4) ~R 3&E
3(5) ~R∨~S 4∨I
3(6) ~(R&S) 5ド・モルガンの法則
23(7)~Q 26MTT
123(8)~P 17MTT
3(9) S 3&E
123(ア)~P&S 78&I
従って、
(01)(02)により、
(03)
(ⅰ)「脱水」 ならば、「血液濃縮」が起こる。 然るに、
(ⅱ)「血液濃縮」により、「赤血球数と尿酸値」が「上昇」する。 然るに、
(ⅲ)「赤血球数」は「上昇」してゐないが、「尿酸値」は「上昇」してゐる。従って、
(ⅳ)「脱水」以外の「原因」で、「尿酸値」が、「上昇」してゐる。
といふ「推論」は、『妥当』である。
然るに、
(04)
従って、
(03)(04)により、
(05)
「患者(ID0000123456)」に関しては、 「尿酸値の上昇の原因」は、「脱水」ではない。
従って、
(05)により、
(06)
「S医師」による、
8.入院日(2018/12/21) の尿酸値は10.3と高値であり、 入院の原因となった痛風発作の原因と考えられます。 入院後、 輸液等を行い高尿酸血症に対する薬剤の投与がなくとも尿酸値は低(2018/12/26:7.7 2019/1/4:7.0)し正常範囲内に改善しましたが、これは入院後に行った輸液治療により入院前に存在していた脱水状態が改善され血中物質が希釈された効果により尿酸値も低下したことも一因であると考えます。
といふ『誤診』は、「検査結果」を見ようともしないことによる、『注意義務違反(過失)』である。
然るに、
(07)
(a)
(ⅰ)「脱水」ならば、「赤血球数と尿酸値」が「上昇」する。 然るに、
(ⅱ)「赤血球数」は、「上昇」していない。 然るに、
(ⅲ)「尿酸値」 は、「上昇」してゐる。 従って、
(ⅳ)「脱水」でないとは限らない。
といふ「間違った推論」は、「何となく、正しい」やうにも、思へないでもない。
然るに、
(08)
(b)
(ⅰ)「鈴木氏」ならば、「男性の医師」である。然るに、
(ⅱ)「その人」は、 「女性」 である。然るに、
(ⅲ)「その人」は、 「医師」である。従って、
(ⅳ)「鈴木氏」でないとは限らない。
といふ「間違った推論」は、「どう考へても、マチガイ」である。
然るに、
(06)(07)により、
(08)
「推論(a)」も、
「推論(b)」も、『形式』としては、
(ⅰ) P→Q&R 然るに、
(ⅱ) ~Q 然るに、
(ⅲ) R 従って、
(ⅳ)~Pであるとは限らない。
といふ『形式』であるため、『同じ』である。
従って、
(06)(07)(08)により、
(09)
「我々」は必ずしも、『推論の形式』だけに従って、「推論」をしてゐるわけではなく、そのため、
(ⅰ)「脱水」ならば、「赤血球数と尿酸値」が「上昇」する。 然るに、
(ⅱ)「赤血球数」は、「上昇」していない。 然るに、
(ⅲ)「尿酸値」 は、「上昇」してゐる。 従って、
(ⅳ)「脱水」でないとは限らない。
といふ「正しくない推論」であっても、「医師」が、「そのやうに言った」場合は、
「何となく、正しい」やうに、思ふことになる。
(01)
① 同一律。すなはち、
① P→P。すなはち、
① Pであるならば、Pである。
といふ「命題」は、「同語反復(トートロジー)」であって、「恒真命題(トートロジー)」である。
然るに、
(02)
(ⅰ)
1 (1) P→ P A
2 (2) P&~P A
2 (3) P 2&E
12 (4) P 13MPP
2 (5) ~P 2&E
12 (6) P&~P 45&I
1 (7)~(P&~P) 26RAA
(ⅱ)
1 (1)~(P&~P) A
2 (2) P A
3(3) ~P A
23(4) P&~P 23&I
123(5)~(P&~P)&
(P&~P) 14&I
12 (6) ~~P 35RAA
12 (7) P 6DN
1 (8) P→ P 2CP
(03)
(ⅱ)
1 (1) ~(P&~P) A
2 (2) ~(P∨~P) A
3 (3) ~P A
3 (4) P∨~P 3∨I
23 (5) ~(P∨~P)&
(P∨~P) 14&I
2 (6) ~~P 35RAA
2 (7) P 6DN
8(8) P A
8(9) P∨~P 8∨I
2 8(ア) ~(P∨~P)&
(P∨~P) 28&I
2 (イ) ~P 8アRAA
2 (ウ) P&~P 7イ&I
12 (エ) ~(P&~P)&
(P&~P) 1ウ&I
1 (オ)~~(P∨~P) 2エRAA
(カ) P∨~P オDN
(ⅲ)
1 (1) P∨~P A
2 (2) P&~P A
3 (3) P A
2 (4) ~P 2&E
23 (5) P&~P 34&I
3 (6)~(P&~P) 25RAA
7(7) ~P A
2 (8) P 2&E
2 7(9) P&~P 78&I
7(ア)~(P&~P) 29RAA
1 (イ)~(P&~P) 1367ア∨E
従って、
(02)(03)により、
(04)
① P→ P
② ~(P&~P)
③ P∨~P
に於いて、すなはち、
① Pであるならば、Pである。
②(Pであって、Pでない)といふことはない。
③ Pであるか、または、Pでない。
①=②=③ である。
従って、
(01)(04)により、
(05)
① P→ P
② ~(P&~P)
③ P∨~P
に於いて、3つとも、
①「トートロジー(同語反復・恒真命題)」。
②「トートロジー(同語反復・恒真命題)」。
③「トートロジー(同語反復・恒真命題)」。
である。
然るに、
(06)
(ⅰ)
1(1)P A
(2)P→P 11CP
(ⅱ)
1(1) P&~P A
(2)~(P&~P) 11RAA
(ⅲ)
1 (1) ~(P∨~P) A
2(2) P A
2(3) P∨~P 2∨I
12(4) ~(P∨~P)&
(P∨~P) 13&I
1 (5) ~P 24RAA
1 (6) P∨~P 5∨I
1 (7) ~(P∨~P)&
(P∨~P) 12&I
(8)~~(P∨~P) 17RAA
(9) P∨~P 8DN
従って、
(07)
①├ P→ P
②├ ~(P&~P)
③├ P∨~P
といふ「証明可能な連式」、すなはち、
①├ 同一律
②├ 矛盾律
③├ 排中律
に於いて、これらは、3つとも、
① 仮定(assumptions)の数が0である所の、証明可能(provable)な連式(sequent)の結論(conclusion)。
② 仮定(assumptions)の数が0である所の、証明可能(provable)な連式(sequent)の結論(conclusion)。
③ 仮定(assumptions)の数が0である所の、証明可能(provable)な連式(sequent)の結論(conclusion)。
である。
従って、
(07)により、
(08)
「トートロジー(同語反復・恒真命題)」とは、
「仮定の数が0である所の、証明可能な連式の結論」である。
従って、
(08)により、
(09)
「仮定の数が2である所の、証明可能な連式の結論」は、
「トートロジー(同語反復・恒真命題)」ではない。
然るに、
(10)
(ⅳ)
1 (1)P→Q A
2(2)P A
12(3) Q 12MPP
従って、
(10)により、
(11)
④ P→Q,P├ Q
に於いて、
④ Q は、
④「仮定の数が2である所の、証明可能な連式の結論」であって、
④「仮定の数が0である所の、証明可能な連式の結論」ではない。
従って、
(07)~(11)により、
(12)
①├ P→ P
②├ ~(P&~P)
③├ P∨~P
④ P→Q,P├ Q
といふ「証明可能な連式」、すなはち、
① 同一律
② 矛盾律
③ 排中律
④ モーダスポネンス
に於いて、
④ だけが、「トートロジー(同語反復・恒真命題)」ではない。
然るに、
(13)
(ⅴ)
1 (1) P→Q A
2(2) P A
12(3) Q 12
1 (4) P→Q 23CP
(5)(P→Q)→(P→Q) 14CP
(〃)(PならばQ)ならば(PならばQ) 14CP
従って、
(13)により、
(14)
④ P→Q,P├ Q
⑤├(P→Q)→(P→Q)
に於いて、
④ ならば、⑤ である。
従って、
(12)(13)(14)により、
(15)
①├ P→ P
②├ ~(P&~P)
③├ P∨~P
④ P→Q,P├ Q
⑤├(P→Q)→(P→Q)
といふ「証明可能な連式」、すなはち、
① 同一律
② 矛盾律
③ 排中律
④ モーダスポネンス
⑤ 同一律
に於いて、
④ だけが、「トートロジー(同語反復・恒真命題)」ではないにしても、
④ ならば、
⑤「同一律(同語反復)」である。
然るに、
(16)
(ⅰ)窃かに君の車に駕する者は罪として刖せらる。
(ⅱ)窃かに君の車に駕す。故に、
(ⅲ)罪として刖せらる。
といふやうな「推論」を、「法的三段論法」とする。
然るに、
(17)
P=窃かに君の車に駕す。
Q=罪として刖せらる。
とするならば、
(ⅰ)窃かに君の車に駕する者は罪として刖せらる。
(ⅱ)窃かに君の車に駕す。故に、
(ⅲ)罪として刖せらる。
といふやうな「推論」は、
(ⅰ)P→Q
(ⅱ)P├
(ⅲ)Q
に、他ならない。
従って、
(16)(17)により、
(18)
(ⅰ)窃かに君の車に駕する者は罪として刖せらる。
(ⅱ)窃かに君の車に駕す。故に、
(ⅲ)罪として刖せらる。
といふ「法的三段論法」は、
④ P→Q,P├ Q
であるところの、
④ モーダスポネンス(modus ponens)
である。
従って、
(15)(18)により、
(19)
「法律家」が所謂、「法的三段論法」といふのは、 「論理学者」が所謂、「モーダスポネンス」に他ならない。
従って、
(19)により、
(20)
「法的三段論法」に従って、「判決」が下される以上、
「法律家」は、「論理学」を、無視しては、ならない。
然るに、
(21)
(ⅰ)
1 (1) P&~P A
(2) ~(P&~P) 11RAA
(3) ~(P&~P)∨ Q 2∨I
4 (4) (P&~P)&~Q A
5 (5) ~(P&~P) A
4 (6) (P&~P) 4&E
45 (7) ~(P&~P)&
(P&~P) 56&I
5 (8)~{(P&~P)&~Q} 47RAA
9 (9) Q A
4 (ア) ~Q 4&E
4 9 (イ) Q&~Q 9ア&I
9 (ウ)~{(P&~P)&~Q} 4イRAA
(オ)~{(P&~P)&~Q} 3589ウ
カ (カ) (P&~P) A
キ(キ) ~Q A
カキ(ク) (P&~P)&~Q カキ&I
カキ(ケ)~{(P&~P)&~Q}&
(P&~P)&~Q オク&I
カ (ケ) ~~Q キケRAA
カ (コ) Q ケDN
(サ) (P&~P)→ Q カコCP
(ⅱ)
1 (1) P&~P A
(2) ~(P&~P) 11RAA
(3) ~(P&~P)∨~Q 2∨I
4 (4) (P&~P)& Q A
5 (5) ~(P&~P) A
4 (6) (P&~P) 4&E
45 (7) ~(P&~P)&
(P&~P) 56&I
5 (8)~{(P&~P)& Q} 47RAA
9 (9) ~Q A
4 (ア) Q 4&E
4 9 (イ) ~Q&Q 9ア&I
9 (ウ)~{(P&~P)& Q} 4イRAA
(オ)~{(P&~P)& Q} 3589ウ
カ (カ) (P&~P) A
キ(キ) Q A
カキ(ク) (P&~P)& Q カキ&I
カキ(ケ)~{(P&~P)& Q}&
(P&~P)& Q オク&I
カ (ケ) ~Q キケRAA
カ (コ) ~Q ケDN
(サ) (P&~P)→~Q カコCP
従って、
(08)(21)により、
(22)
①├(P&~P)→ Q
②├(P&~P)→~Q
に於いて、
① は「トートロジー(恒真式)」であって、同時に、
② も「トートロジー(恒真式)」である。
従って、
(22)により、
(23)
①(矛盾)が「真」であるならば、Qは「真」であって、
②(矛盾)が「真」であるならば、Qは「偽」である。
然るに、
(24)
「真であって、偽である」といふことは、「有り得ない」。
従って、
(19)(23)(24)により、
(24)
「同じ法的問題に人によって異なる答えが出されること」があるとすれば、
「どちらか一方」が、
①├(矛盾)→ Q
②├(矛盾)→~Q
といふ「トートロジー」を「主張」してゐる。
従って、
(24)により、
(25)
「同じ法的問題に人によって異なる答えが出されること」があるとすれば、
「少なくとも、どちらか一方の主張」が、「矛盾」してゐる。
従って、
(01)~(25)により、
(26)
「論理的」には、
法的判断の正しさと真理の整合説、そして問答
早瀬 勝明 (甲南大学)
法的な問題に正しい答えはあるか。法的三段論法は機械的形式的に唯一の結論を導くわけ
ではなく、同じ法的問題に人によって異なる答えが出されることは、よく知られた事実で
ある。複数の答えが提出されたとき、いずれかが正しいのか。それとも、複数の答えが出
てくる法的問題に正しい答えなどなく、どれが正しいのかと問うこと自体が間違いなのか。
といふ「問ひかけ」は、「成立」しない。
(27)
「複数の矛盾した答え」が「導出」されるとすれば、「論理的」には、
「少なくとも、どちらか一方の主張」が「矛盾」してゐる。
といふことは、「疑ふ余地が無い」。
(01)
1 (1) P A
1 (2) P∨ Q 1∨I
3 (3) ~P&~Q A
4 (4) P A
3 (5) ~P 3&E
34 (6) P&~P 45&I
4 (7) ~(~P&~Q) 36RAA
8 (8) Q A
3 (9) ~Q 3&E
3 8 (ア) Q&~Q 89&I
8 (イ) ~(~P&~Q) 3アRAA
1 (ウ) ~(~P&~Q) 2478イ∨E
エ (エ) ~P A
オ (オ) ~Q A
エオ (カ) ~P&~Q エオ&I
1 エオ (キ) ~(~P&~Q)&
(~P&~Q) ウカ&I
1 エ (ク) ~~Q オキRAA
1 エ (ケ) Q ケDN
1 (コ) ~P→ Q エケCP
(サ)P→(~P→ Q) 1コCP
シ(シ)P& ~P A
シ(ス)P シ&E
シ(セ) ~P→ Q サスMPP
シ(ソ) ~P シ&E
シ(タ) Q セソMPP
(チ)(P&~P)→Q シCP
従って、
(01)により、
(02)
├(P&~P)→Q
といふ「連式」は、「恒真式(トートロジー)」である。
従って、
(02)により、
(03)
(Pであって、Pでない)ならばQである。
といふ「命題」は、
(任意のPとQ)に於いて「真」である。
然るに、
(04)
(矛盾)とは、「語源(韓非子)」から言っても、
(Pであって、Pでない)といふことを言ふ。
従って、
(03)(04)により、
(05)
「矛盾」が「真」であるならば、「任意の命題」が「真」である。
然るに、
(06)
「任意の命題」の「否定命題」も、
「任意の命題」である。
従って、
(04)(05)(06)により、
(07)
「矛盾」が「真」であるならば、
「任意の命題」は「真」であると「同時」に「偽」であるが、今も書いた通リ、
「矛盾」とは、 「真」であると「同時」に「偽」であることを言ふ。
従って、
(07)により、
(08)
「矛盾」を「認めない」のであれば、
「同じ法的問題に人によって異なる答えが出されること」があるとすれば、
『少なくとも、どちらか一方の答えが、「真」ではない。』
然るに、
(09)
法的判断の正しさと真理の整合説、そして問答
早瀬 勝明 (甲南大学)
法的な問題に正しい答えはあるか。法的三段論法は機械的形式的に唯一の結論を導くわけ
ではなく、同じ法的問題に人によって異なる答えが出されることは、よく知られた事実で
ある。複数の答えが提出されたとき、いずれかが正しいのか。それとも、複数の答えが出
てくる法的問題に正しい答えなどなく、どれが正しいのかと問うこと自体が間違いなのか。
従って、
(08)(09)により、
(10)
おそらくは、大半の「法律家」は、
あるいは、「論理」といふものに、「興味」が無い(!?)。
と思っていたら、
(11)
いずれにしろ、法律家の言う論理というものが、他の分野で言う論理とは全く別のもので、
結局のところ、紛争解決のための修辞に過ぎないということは、
法律家と接する人も知っておいたほうがよいのではないかと思います。
(横浜の弁護士ブログ)
といふ『ブログ』を、発見した。
(01)
(ⅰ)
1 (1) P∨ Q∨ R A
2 (2) ~P&~Q&~R A
1 (3) (P∨ Q)∨R 1結合法則
4 (4) (P∨ Q) A
5 (5) P A
2 (6) ~P 2&E
2 5 (7) P&~P 56&I
5 (8)~(~P&~Q&~R) 27RAA
9 (9) Q A
2 (ア) ~Q 2&E
2 9 (イ) Q&~Q 9ア&I
9 (ウ)~(~P&~Q&~R) 2イRAA
4 (エ)~(~P&~Q&~R) 4589ウ∨E
オ(オ) R A
2 (カ) ~R 2&E
2 オ(キ) R&~R オカ&I
オ(ク)~(~P&~Q&~R) 2キRAA
1 (ケ)~(~P&~Q&~R) 34エオク∨E
(ⅱ)
1 (1)~(~P&~Q&~R) A
2 (2) ~(P∨ Q∨ R) A
3 (3) P A
3 (4) P∨ Q 3∨I
3 (5) P∨ Q∨ R 4∨I
23 (6) ~(P∨ Q∨ R)&
(P∨ Q∨ R) 25&I
2 (7) ~P 36RAA
8 (8) Q A
8 (9) P∨ Q 8∨I
ア (ア) P∨ Q∨ R 9∨I
2 ア (イ) ~(P∨ Q∨ R)&
(P∨ Q∨ R) 2ア&I
2 (ウ) ~Q アイRAA
エ(エ) R A
エ(オ) Q∨ R エ∨I
エ(カ) P∨ Q∨ R オ∨I
2 エ(キ) ~(P∨ Q∨ R)&
(P∨ Q∨ R) 2カ&I
2 (ク) ~R エキRAA
2 (ケ) ~P&~Q 7ウ&I
2 (コ) ~P&~Q&~R クケ&I
12 (サ)~(~P&~Q&~R)&
(~P&~Q&~R) 1コ&I
1 (シ)~~(P∨ Q∨ R) 2サRAA
1 (ス) (P∨ Q∨ R) シDN
従って、
(01)により、
(02)
① P∨ Q∨ R
② ~(~P&~Q&~R)
に於いて、
①=② は「ド・モルガンの法則」である。
従って、
(02)により、
(03)
P=~P
Q=~Q
R=~R
といふ「代入」により、
① ~P∨ ~Q∨ ~R
② ~(~~P&~~Q&~~R)
に於いて、
①=② は「ド・モルガンの法則」である。
従って、
(03)により、
(04)
「二重否定」により、
① ~P∨~Q∨~R
② ~(P& Q& R)
に於いて、
①=② は「ド・モルガンの法則」である。
従って、
(04)により、
(05)
① 3人の内、少なくとも、一人は「ウソ」を付いている。
②(3人が、3人とも「本当」のことを言っている)といふわけではない。
に於いて、
①=② である。
といふことは、『論理学』としても、「正しい」。
従って、
(04)(05)により、
(06)
① 4人の内、少なくとも、一人は「ウソ」を付いている。
②(4人が、4人とも「本当」のことを言っている)といふわけではない。
に於いて、
①=② である。
といふことは、『論理学』としても、「正しい」。
従って、
(04)(05)(06)により、
(07)
① ~P∨~Q∨~R∨~S
② ~(P& Q& R& S)
に於いて、
①=② は「ド・モルガンの法則」である。
然るに、
(08)
1 (1) P→Q A
2 (2) P→R A
3 (3) P→S A
4 (4) P→T A
5 (5) P A
12 (6) Q 15MPP
1 3 (7) R 25MPP
1 4 (8) S 35MPP
1 5 (9) T 45MPP
123 (ア) Q&R 67&I
1234 (イ) Q&R&S 8ア&I
12345 (ウ) Q&R&S&T 9イ&I
1234 (エ) P→(Q&R&S&T) 5ウCP
オ(オ) ~Q A
オ(カ) ~Q∨~P オ∨I
オ(キ) ~Q∨~R∨~S カ∨I
オ(ク) ~Q∨~R∨~S∨~T キ∨I
オ(ケ) ~(Q&R&S&T) ク、ド・モルガンの法則
1234 オ(コ)~P エケMTT
従って、
(08)により、
(09)
① Pならば、Qであり、
② Pならば、Rであり、
③ Pならば、Sであり、
④ Pならば、Tである。然るに、
⑤ Qではない。 従って、
⑥ Pでない。
といふ「推論」は「妥当」である。
従って、
(09)により、
(10)
①「脱水」ならば、「赤血球数は上昇する。」
②「脱水」ならば、「ヘモグロビンも上昇する。」
③「脱水」ならば、「ヘマトクリットも上昇する。」
④「脱水」ならば、「尿酸値も上昇する。」然るに、
⑤「赤血球数・他は、上昇してゐない」。 従って、
⑥「脱水」でない。
といふ「推論」は「妥当」である。
然るに、
(11)
(12)
従って、
(11)(12)により、
(13)
『事実』として、
①「脱水」ならば、「赤血球数は上昇する。」
②「脱水」ならば、「ヘモグロビンも上昇する。」
③「脱水」ならば、「ヘマトクリットも上昇する。」
④「脱水」ならば、「尿酸値も上昇する。」
然るに、
(14)
従って、
(14)により、
(15)
(ⅰ)2018年07月31日(3カ月毎の定期検査)
(ⅱ)2018年10月23日(3カ月毎の定期検査)
(ⅲ)2018年12月13日(痛風発作で通院)
(ⅳ)2018年12月21日(痛風発作で入院)
といふ「直近の4回の血液検査」に於いて、
といふ「持病」が有った「私の父」の、
(a)「赤血球数・ヘモグロビン・ヘマトクリット」は、「平均で、約0.5%、下降してゐる」ものの、その一方で、
(b)「尿酸値」に関しては、「最終的に、約26%の上昇」が「確認」出来る。
従って、
(10)~(15)により、
(16)
①「私の父が、脱水」ならば、「私の父の、赤血球数は上昇する。」
②「私の父が、脱水」ならば、「私の父の、ヘモグロビンも上昇する。」
③「私の父が、脱水」ならば、「私の父の、ヘマトクリットも上昇する。」
④「私の父が、脱水」ならば、「私の父の、尿酸値も上昇する。」然るに、
⑤「私の父の、赤血球数・他は、上昇してゐない」。 従って、
⑥「私の父は、脱水」ではない。
といふ「推論」は「妥当」であって、尚且つ、
⑥「私の父は、脱水」ではない。
といふ「結論」は、「真(本当)」である。
然るに、
(17)
「鈴木医師」曰く、
8.入院日(2018/12/21) の尿酸値は10.3と高値であり、入院の原因となった痛風発作の原因と考えられます。 入院後、 輸液等を行い高尿酸血症に対する薬剤の投与がなくとも尿酸値は低下 (2018/12/26:7.7 2019/1/4:7.0) し正常範囲内に改善しましたが、これは入院後に行った輸液治療により入院前に存在していた脱水状態が改善され 血中物質が希釈された効果により尿酸値も低下したことも一因であると考えます。
従って、
(11)(14)(15)により、
(18)
といふ「検査結果」、すなはち、
(ⅰ)2018年07月31日(3カ月毎の定期検査)
(ⅱ)2018年10月23日(3カ月毎の定期検査)
(ⅲ)2018年12月13日(痛風発作で通院)
(ⅳ)2018年12月21日(痛風発作で入院)
といふ「直近の4回の血液検査」に於いて、
(b)「尿酸とクレアチニン」は、「上昇している」が、その間にあって、
(a)「赤血球数」は、「下降してゐる」。
といふことからすれば、
『入院前に存在していた脱水状態』
は、有り得ないにも拘わらず、「鈴木医師」は、
『入院前に存在していた脱水状態』
といふ『誤診』を犯してゐる。
然るに、
(19)
「Bingチャト(生成AI)」に、「誤診率」を「質問」したところ、
従って、
(19)により、
(20)
「誤診」を犯さない「医師」はゐない。
ということからすると、「誤診」自体を「理由」に、「医師が糾弾されることは無い」はずあり、因みに、「白い巨塔(フジTV)の財前五郎」も、「(不可抗力による)誤診」そのものでは「有罪」にはならず、「一審」では「無罪」になってゐる。
然るに、
(14)(15)により、
(21)
「父の持病」は、
①「悪性貧血」と、
②「痛風」と、
③「慢性腎臓病」である。
といふ「事情」により、
①「赤血球(の推移)」と、
②「尿酸値(の推移)」と、
③「クレアチニン(の推移)」
に「注意」をしないのであれば、
④「わざわざ、3カ月に1度、血液検査」をする「必要」はない。
従って、
(11)(15)(17)(18)(21)により、
(22)
「実際」には、
①「赤血球」は「下降」してゐる。
②「尿酸値」は「上昇」し、
③「クレアチニン」も「上昇」してゐる。
にも拘らず、
8.入院日(2018/12/21) の尿酸値は10.3と高値であり、入院の原因となった痛風発作の原因と考えられます。 入院後、 輸液等を行い高尿酸血症に対する薬剤の投与がなくとも尿酸値は低下 (2018/12/26:7.7 2019/1/4:7.0) し正常範囲内に改善しましたが、これは入院後に行った輸液治療により入院前に存在していた脱水状態が改善され 血中物質が希釈された効果により尿酸値も低下したことも一因であると考えます。
といふ「回答」を私に対して行ふといふことは、要するに、
「父の持病」は、
①「悪性貧血」と、
②「痛風」と、
③「慢性腎臓病」であったにも、拘わらず、
といふ「(最も注意が必要な)検査結果」を「確認」しなかった。
といふことを、「自白」している、といふことに、他ならない。
然るに、
(23)
「Bingチャット」に、
「血液検査の見落とし」と、「医師の過失とは」と、「質問」したたところ、
との、ことである。
従って、
(20)(23)により、
(24)
「過失」=「注意義務違反」であって、
「血液検査の見落とし」は、「注意義務違反」であり、
そのため、「検査結果の見落とし」は、「過失」であるが、
「誤診」自体は、「過失」ではない。
従って、
(22)(24)により、
(25)
この場合、「誤診は、過失の必要条件であって、十分条件でない」が、
「注意義務違反」であるため、すなはち、「過失」である。
(01)
(02)
従って、
(01)(02)により、
(03)
「脱水であるならば、(赤血球、ヘモグロビン、ヘマトクリット、尿酸値)等が上昇する。」
然るに、
(04)
P=脱水である。
Q=赤血球数・ヘモグロビン・ヘマトクリットが上昇する。
R=尿酸値が上昇する。
とする。
従って、
(01)~(04)により、
(05)
①「脱水であるならば、(赤血球・ヘモグロビン・ヘマトクリット、尿酸値)等が上昇する。」
②「P→Q&R」
に於いて、
①=② である。
然るに、
(06)
(ⅱ)
1 (1) P→Q&R A
2 (2) ~Q A
2 (3) ~Q∨~R 2∨I
2 (4) ~(Q&R) 3ド・モルガンの法則
12 (5)~P 14MTT
1 (6) ~Q→~P 25CP
従って、
(06)により、
(07)
②「P→Q&R」
③「~Q→~P」
に於いて、
②⇒③ である。
従って、
(05)(07)により、
(08)
①「脱水であるならば、(赤血球・ヘモグロビン・ヘマトクリット、尿酸値)等が上昇する。」
②「P→Q&R」
③「~Q→~P」
に於いて、
①=② であって、
②⇒③ である。
従って、
(04)(08)により、
(09)
①「脱水であるならば、(赤血球・ヘモグロビン・ヘマトクリット、尿酸値)等が上昇する。」
③「(赤血球数・ヘモグロビン・ヘマトクリットが上昇していない)ならば、脱水ではない。」
に於いて、
① ならば、③ である。
従って、
(09)により、
(10)
(ⅰ)脱水であるならば、(赤血球・ヘモグロビン・ヘマトクリット、尿酸値)等が上昇する。従って、
(ⅱ)(赤血球数・ヘモグロビン・ヘマトクリットが上昇していない)ならば、脱水ではない。然るに、
(ⅲ)(赤血球数・ヘモグロビン・ヘマトクリットが上昇していない)。 従って、
(ⅳ)脱水ではない。
という『推論』は、『妥当』である。
然るに、
(11)
従って、
(11)により、
(12)
2018年07月18日(定期検査)から、
2018年12月21日(入院当日)にかけて、
(ⅰ)(赤血球数・ヘモグロビン・ヘマトクリット)は、「約0.5%下降している」のに対して、
(ⅱ)「尿酸値」には、「約26%の上昇」が「確認」出来る。
従って、
(10)(11)(12)により、
(13)
2018年07月18日(定期検査)から、
2018年12月21日(入院当日)にかけて、
(ⅳ)「脱水が有った」という「事実」は無い。
従って、
(12)(13)により、
(14)
「脱水が有った」という「事実」は無いが「故に」、「必然的」に、
「高尿酸血症(痛風発作の原因)」の「原因」は、「脱水」ではない。
従って、
(14)により、
(15)
という『診断(脱水状態)』は、
という「検査結果」と、『矛盾』する。
従って、
(16)
「S医師(総合病院の副院長)」は、「(約1カ月後、退院したその日に死亡した)私の父」を「診断」した際に、
「直近の血液検査」さえも、「確認していなかった」ということは、「疑う余地」が無い。
(01)
①{P }ならば{Pである}。
②{P&Q}ならば{Pである}。
といふ「演繹推理」に於いて、
① ならば、② である。
従って、
(01)により、
(02)
演繹推理では、前提を追加しても結論は不変である。結論は前提に含まれるものだけを導出するため、
新前提を加えても、これらによって結論が変わるわけではないからである。
(岩波全書、論理学入門、1979年、156頁)
然るに、
(03)
(a)
1 (1)∀x{象x→∀z(~鼻zx→~長z)} A
2 (2)∀x{兎x→∃z(~鼻zx& 長z)} A
3 (3)∃x(象x&兎x) A
1 (4) 象a→∀z(~鼻za→~長z)} 1UE
2 (5) 兎a→∃z(~鼻za& 長z)} 2UE
6 (6) 象a&兎a A
6 (7) 象a 6&E
6 (8) 兎a 6&E
1 6 (9) ∀z(~鼻za→~長z) 47MPP
2 6 (ア) ∃z(~鼻za& 長z) 58MPP
1 6 (イ) ~鼻ba→~長b 9UE
ウ (ウ) ~鼻ba& 長b A
ウ (エ) ~鼻ba ウ&E
1 6ウ (オ) ~長b イエMPP
ウ (カ) 長b ウ&E
1 6ウ (キ) ~長b&長b オア&I
12 6 (ク) ~長b&長b アウキEE
123 (ケ) ~長b&長b 36クEE
12 (コ)~∃x(象x&兎x) 3ケRAA
12 (サ)∀x~(象x&兎x) コ量化子の関係
12 (シ) ~(象a&兎a) サUE
ス (ス) 象a A
セ(セ) 兎a A
スセ(ソ) 象a&兎a スセ&I
12 スセ(タ) ~(象a&兎a)&(象a&兎a) シソ&I
12 ス (チ) ~兎a セRAA
12 (ツ) 象a→~兎a スチCP
12 (テ)∀x(象x→~兎x) ツUI
(b)
1 (1) ∀x{象x→∃y(鼻yx&長y)&∀z(~鼻zx→~長z)} A
2 (2) ∀x{兎x→∃z(耳zx&~鼻zx&長z)} A
3 (3) ∃x(象x&兎x) A
1 (4) 象a→∃y(鼻ya&長y)&∀z(~鼻za→~長z) 1UE
2 (5) 兎a→∃z(耳za&~鼻za&長z) 2UE
6 (6) 象a&兎a A
6 (7) 象a 6&E
6 (8) 兎a 6&E
1 6 (9) ∀z(~鼻za→~長z) 47MPP
1 6 (ア) ~鼻ba→~長b 9UI
2 6 (イ) ∃z(耳za&~鼻za&長z) 58MPP
ウ (ウ) 耳ba&~鼻ba&長b A
ウ (エ) ~鼻ba ウ&E
ウ (オ) 長b ウ&E
1 6ウ (カ) ~長b アエMPP
1 6ウ (キ) 長b&~長b オカ&I
12 6 (ク) 長b&~長b イウキEE
123 (ケ) 長b&~長b 36クEE
12 (コ)~∃x(象x&兎x) 3ケRAA
12 (サ)∀x~(象x&兎x) コ量化子の関係
12 (シ) ~(象a&兎a) サUE
ス (ス) 象a A
セ(セ) 兎a A
スセ(ソ) 象a&兎a スセ&I
12 スセ(タ) ~(象a&兎a)&(象a&兎a) シソ&I
12 ス (チ) ~兎a セタRAA
12 (ツ) 象a→~兎a スチCP
12 (テ)∀x(象x→~兎x) ツUI
従って、
(01)(02)(03)により、
(04)
『演繹推理では、前提を追加しても結論は不変である。』
といふ「理由」により、
① ∀x{象x→∀z(~鼻zx→~長z)}。然るに、
② ∀x{兎x→∃z(~鼻zx& 長z)}。従って、
③ ∀x(象x→~兎x)。
といふ「推論」は、「事実上」、
④ ∀x{象x→∃y(鼻yx&長y)&∀z(~鼻zx→~長z)}。然るに、
⑤ ∀x{兎x→∃z(耳zx&~鼻zx&長z)}。従って、
⑥ ∀x(象x→~兎x)。
といふ「推論」に、「等しい」。
従って、
(04)により、
(05)
① すべてのxについて{xが象であるならば、すべてのzについて(zがxの鼻ではないならば、zは長くない)}。
② すべてのxについて{xが兎であるならば、あるzは(xの鼻ではないが、zは長い)}。
③ すべてのxについて(xが象であるならば、xは兎ではない)。
といふ「推論」は、「事実上」、
④ すべてのxについて{xが象であるならば、あるyは(xの鼻であって、長く)、すべてのzについて(zがxの鼻ではないならば、zは長くない)}。
⑤ すべてのxについて{xが兎であるならば、あるzは(xの耳であって、長いが、zは鼻ではない)}。
⑥ すべてのxについて(xが象であるならば、xは兎ではない)。
といふ「推論」に、「等しい」。
従って、
(02)(04)(05)により、
(06)
④ 象は鼻が長い。 然るに、
⑤ 兎の耳は長いが、耳は鼻ではない。従って、
⑥ 象は兎ではない。
といふ「推論」は、「事実上」、
① 象は、鼻以外は長くない。然るに、
② 兎は、鼻以外が長い。従って、
③ 象は兎ではない。
といふ「推論」に、「等しい」。
従って、
(06)により、
(07)
④ 象は鼻が長い。 然るに、
⑤ 兎の耳は長いが、耳は鼻ではない。従って、
⑥ 象は兎ではない。
といふ「推論」が「妥当」であるならば、
④ 象は鼻が長い。
といふ「日本語」は、「必然的」に、
① 象は、鼻以外は長くない。
といふ「意味」を「含意」する。
然るに、
(08)
④ 象は鼻が長い。 然るに、
⑤ 兎の耳は長いが、耳は鼻ではない。従って、
⑥ 象は兎ではない。
といふ「推論」は「妥当」である。
従って、
(07)(08)により、
(09)
④ 象は鼻が長い。
といふ「日本語」は、「必然的」に、
① 象は鼻以外は長くない。
といふ「意味」を「含意」する。
従って、
(04)(05)(09)により、
(10)
① 象は鼻が長い。⇔
① 象は鼻は長く、鼻以外は長くない。⇔
① ∀x{象x→∃y(鼻yx&長y)&∀z(~鼻zx→~長z)}。⇔
① すべてのxについて{xが象であるならば、あるyは(xの鼻であって、長く)、すべてのzについて(zがxの鼻ではないならば、zは長くない)}。
といふ「等式」が、「成立」する。
―「昨日の記事(令和5年6月9日)」を書き換えます。―
(01)
① 象之鼻(漢文)
② 象の鼻(訓読)
に於いて、
①=② である。
然るに、
(02)
① 象鼻(漢文)
② 象の鼻(訓読)
であっても、
①=② である。
従って、
(02)により、
(03)
① 象鼻長(漢文)。
② 象の鼻は長し(訓読)。
に於いて、
①=② である。
然るに、
(04)
主語・述語の順序で並べた文章で、
述語の上に置かれる語が一つの主語ではなく、主語が重なっている場合がある。
(角川ソフィア文庫、漢文の語法、2023年、184頁)
従って、
(03)(04)により、
(05)
① 象鼻長(漢文)。
② 象の鼻は長し(訓読)。
③ 象は、鼻長し(訓読)。
に於いて、
①=② であるか、または、
①=③ である。
従って、
(01)~(05)により、
(06)
① 象鼻長(漢文)。
② 象の鼻は、長い(口語)。
③ 象は、鼻は長い(口語)。
④ 象は、鼻が長い(口語)。
に於いて、
①=② であるか、
①=③ であるか、
①=④ である。
然るに、
(07)
① 象者動物也。
② 象は動物である。
③ Elephants are animals.
④ ∀x(象x→動物x).
⑤ For all x,if 象x then 動物x.
⑥ すべてのxについて、xが象であるならば、xは動物である。
に於いて、
①=②=③=④=⑤=⑥ である。
然るに、
(08)
日本語で典型的な文(センテンス)は、「Ⅹは」で始まる題述べ関係の文です。公式で一括して、
Ⅹハ、ウンヌン。
題目 述 部
とかくことができます。題目の提示「Ⅹは」は、だいたい「Ⅹニツイテ言エバ」の心持ちです。 (三上章、象は鼻が長い、1960年、8頁)
従って、
(07)(08)により、
(09)
② 象は
④ ∀x(象x→
⑥ すべてのxについて、xが象であるならば、
⑦ 三上先生が言ふ所の「Ⅹニツイテ言エバ」の心持ち。
に於いて、
②=④=⑥=⑦ である。
(01)
(ⅰ)太陽系は、地球が第三惑星である。然るに、
(ⅱ) 火星は、地球ではない。 従って、
(ⅲ)太陽系は、地球は第三惑星であって、火星は第三惑星ではない。
といふ「推論」は「妥当」である。
然るに、
(02)
① 第一惑星は、一つしかないし、
② 第二惑星も、一つしかないし、
③ 第三惑星も、一つしかないし、
④ 第四惑星も、一つしかないし、
⑤ 第五惑星は、一つしかないし、
⑥ 第六惑星も、一つしかないし、
⑦ 第七惑星も、一つしかないし、
⑧ 第八惑星も、一つしかない。
従って、
(02)により、
(03)
③ 第三惑星は、一つしかない。
といふ「理由」により、
(ⅰ)太陽系は、地球が第三惑星である。
といふ「日本語」を、
(ⅰ)太陽系 地球 第三惑星。
といふ『漢文』に「翻訳」したとしても、
(ⅰ)太陽系は、地球が、(唯一の)第三惑星である。
といふ「意味」になる。
cf.
主語・述語の順で並べられた文章で、述語の上に置かれる語が一つの主語だけでなく、
漢 兵 盛。
に於ける、
漢 兵
のやうに、(二つの)主語が重なっている場合がある。
(西田太一郎、漢文の語法、1980年、120頁改)
然るに、
(04)
1 (1)∀x{太陽系x→∃y[地球y&惑星yx&~∃z(z≠y&惑星zx)]} A
1 (2) 太陽系a→∃y[地球y&惑星ya&~∃z(z≠y&惑星za)] 1UE
3 (3) 太陽系a A
13 (4) ∃y[地球y&惑星ya&~∃z(z≠y&惑星za)] 23MPP
5 (5) 地球b&惑星ba&~∃z(z≠b&惑星za) A
5 (6) 地球b&惑星ba 5&E
5 (7) 地球b 6&E
5 (8) 惑星ba 6&E
5 (9) ~∃z(z≠b&惑星za) 5&E
5 (ア) ∀z~(z≠b&惑星za) 9量化子の関係
5 (イ) ~(c≠b&惑星ca) アUE
5 (ウ) ~c≠b∨~惑星ca イ、ド・モルガンの法則
5 (エ) c≠b→~惑星ca ウ含意の定義
オ (オ) ∃z(火星z&~地球z) A
カ (カ) 火星c&~地球c オUE
カ (キ) 火星c カ&E
カ (ク) ~地球c キ&E
5 カ (ケ) 地球b&~地球c 7ク&I
コ(コ) c=b A
5 カコ(サ) 地球b&~地球b ケコ=E
5 カ (シ) c≠b コサRAA
5 カ (ス) ~惑星ca エシMPP
5 カ (セ) 火星c&~惑星ca キス&I
5 カ (ソ) ∃z(火星z&~惑星za) セEI
5オ (タ) ∃z(火星z&~惑星za) オカソEE
5 (チ) ∃y(地球y&惑星ya) 6EI
5オ (ツ) ∃y(地球y&惑星ya)&∃z(火星z&~惑星za) タチ&I
13 オ (テ) ∃y(地球y&惑星ya)&∃z(火星z&~惑星za) 45ツEE
1 オ (ト) 太陽系a→∃y(地球y&惑星yx)&∃z(火星z&~惑星zx) 3テCP
1 オ (ナ)∀x{太陽系x→∃y(地球y&惑星yx)&∃z(火星z&~惑星zx)} トUI
従って、
(04)により、
(05)
(ⅰ)∀x{太陽系x→∃y[地球y&惑星yx&~∃z(z≠y&惑星zx)]}。然るに、
(ⅱ)∃z(火星z&~地球z)。従って、
(ⅲ)∀x{太陽系x→∃y(地球y&惑星yx)&∃z(火星z&~惑星zx)}。
といふ「推論」、すなはち、
(ⅰ)すべてのxについて{xが太陽系であるならば、あるyは[地球であって、xの惑星であって、あるzが(y以外であって、xの惑星である)といふことはない]}。
(ⅱ)あるz(火星であって、地球ではない)。従って、
(ⅲ)すべてのxについて{xが太陽系であるならば、あるyは(地球であって、xの惑星であって)、あるzは(火星であって、xの惑星でない)}。
といふ「推論(の形式)」は、「妥当」である。
従って、
(01)~(05)により、
(06)
(ⅰ)太陽系 地球 惑星。
といふ『漢文』に「相当」する、
(ⅰ)太陽系は、地球が惑星である。
といふ「日本語」が、
(ⅰ)∀x{太陽系x→∃y[地球y&惑星yx&~∃z(z≠y&惑星zx)]}。
(〃)すべてのxについて{xが太陽系であるならば、あるyは[地球であって、xの惑星であって、あるzが(y以外であって、xの惑星である)といふことはない]}。
といふ「意味」であるならば、
(ⅰ)太陽系は、地球が惑星である。
といふ「日本語」は、
(ⅰ)太陽系は、地球以外は惑星でない。
といふ、「意味」になる。
然るに、
(07)
(ⅰ)太陽系 地球 惑星。
に於ける、「地球」を、「殊更に、大きな声」で「発音」したとすれば、
(ⅰ)太陽系 地球 惑星。
といふ「漢文」は、
(ⅰ)太陽系は、地球以外は惑星ではない。
といふ「意味」になったに、「違ひない」。
然るに、
(08)
① 地球は(清音)
② 地球が(濁音)
である。
然るに、
(09)
清音の方は、小さくきれいで速い感じで、コロコロと言うと、ハスの上を水玉がころがるような時の形容である。ゴロゴロと言うと、大きく荒い感じで、力士が土俵でころがる感じである(金田一春彦、日本語(上)、1988年、131頁)。もし濁音を発音するときの物理的・身体的な口腔の膨張によって「濁音=大きい」とイメージがつくられているのだとしたら、面白いですね。この仮説が正しいとすると、なぜ英語話者や中国語話者も濁音に対して「大きい」というイメージを持っているか説明がつきます(川原繁人、音とことばの不思議な世界、2015年、13頁)。
従って、
(08)(09)により、
(10)
① 地球は(清音)
② 地球が(濁音)
であれば、
② の方が、「心理的な音量」が、「大きい」。
従って、
(07)(10)により、
(11)
「我々の先人」が、例へば、
(ⅰ)太陽系 地球 第三惑星。
といふ『漢文』を、
(ⅰ)太陽系は、地球以外は第三惑星でない。
(〃)∀x{太陽系x→∃y[地球y&第三惑星yx&~∃z(z≠y&第三惑星zx)]}。
といふ風に「訳したかった」のであれば、その場合は、
(ⅰ)太陽系は 地球は 第三惑星である。
とはせずに、
(ⅰ)太陽系は 地球が 第三惑星である。
といふ風に、「訳した」はずであり、次第に、「そうした訳」が、「定着」していった。
といふに、「推測」出来る。
(01)
第17節 大主語・提示語・副詞的修飾語
主語・述語の順序で並べられた文章で、述語の上に置かれる語が一つの主語ではなく、主語が重なっている場合がある。
また何かについて述べようとしてその語をまず先に掲げておいて、その次にそれについて具体的に説明する場合がある。
そのほか行為や事件のあった時や所を何の媒介する語もなしで述語より前に置くことがある。
(西田太一郎、漢文の語法、1980年、120頁)
従って、
(01)により、
(02)
① 天皇は、万世一系にして、日本国を統治す。
② 日本国は、万世一系の天皇、これを、統治す。
に於いて、
① 「天皇は」は、「主語」 であり、
②「日本国は」は、「提示語」であるとする。
従って、
(02)により、
(03)
① 寒天は、美味である。
② 寒天は、我、これを食さず。
に於いて、
①「寒天は」は、「主語」 であり、
②「寒天は」は、「提示語」である。
従って、
(03)により、
(04)
① 寒天は、食べません。
② 寒天は、我、これを食さず。
に於いて、
①「寒天は」は、「提示語」であり、
②「寒天は」も、「提示語」である。
然るに、
(05)
② 寒天我不食之=
② 寒天我不〔食(之)〕⇒
② 寒天我〔(之)食〕不=
② 寒天は、我、これを食さず。
といふ「(漢文由来の)日本語」は、「語順」から言っても、
② ∀x{蒟蒻x→∃y(我y&~食yx)}⇔
② すべてのxについて{xが蒟蒻であるならば、あるyは(我であって、yはxを食べない)}。
といふ「述語論理式」に「等しい」。
従って、
(04)(05)により、
(06)
① 寒天は、食べません。
② 寒天は、我、これを食さず。
といふ「日本語」が、「非(述語)論理的」であるといふことはない。
従って、
(06)により、
(07)
① 寒天は、食べません。
② 寒天は、我、これを食さず。
といふ「日本語」に「相当」する『文型』が、「英語」には無いからと言って、
① 寒天は、食べません。
② 寒天は、我、これを食さず。
といふ「日本語」自体が、「非(述語)論理的な言い方」であるといふことには、ならない。
cf.
先日、数人の大学の先生と話をしているときに、ある先生が「うちの学生が、英語ができるようになったら、数学ができるようになった」と言った。これは、暗に、英語ができるようになった、だから数学ができるようになったと言いたいのである。言い換えれば、日本語では論理的に考えられないから、数学ができない、と言いたいのである。私は「またか」と思った。日本人は、この大学の先生のように、日本語は非論理的であり、論理的思考に向いていないと思い込んでいる人が多い。
(月本洋、日本語は論理的である、2009年、2頁)
然るに、
(08)
(ⅱ)
1 (1)~∀x{蒟蒻x→∃y(人y&食yx&~太y)} A
1 (2)∃x~{蒟蒻x→∃y(人y&食yx&~太y)} 1量化子の関係
3 (3) ~{蒟蒻a→∃y(人y&食ya&~太y)} A
3 (4) ~{~蒟蒻a∨∃y(人y&食ya&~太y)} 3含意の定義
3 (5) 蒟蒻a&~∃y(人y&食ya&~太y) 4ド・モルガンの法則
3 (6) 蒟蒻a 5&E
3 (7) ~∃y(人y&食ya&~太y) 5&E
3 (8) ∀y~(人y&食ya&~太y) 7量化子の関係
3 (9) ~(人b&食ba&~太b) 8UE
3 (ア) ~人b∨~食ba∨ 太b 9ド・モルガンの法則
3 (イ) (~人b∨~食ba)∨太b ア結合法則
ウ (ウ) (~人b∨~食ba) A
ウ (エ) ~(人b&食ba) ウ、ド・モルガンの法則
ウ (オ) ~(人b&食ba)∨太b エ∨I
カ(カ) 太b A
カ(キ) ~(人b&食ba)∨太b カ∨I
3 (ク) ~(人b&食ba)∨太b イウオカキ∨E
3 (ケ) (人b&食ba→太b) ク含意の定義
3 (コ) ∀y(人y&食ya→太y) ケUI
3 (サ) 蒟蒻a&∀y(人y&食ya→太y) 6コ&I
3 (シ) ∃x{蒟蒻x&∀y(人y&食yx→太y)} サEI
1 (ス) ∃x{蒟蒻x&∀y(人y&食yx→太y)} 13シEE
(ⅲ)
1 (1) ∃x{蒟蒻x&∀y(人y&食yx→太y)} A
2 (2) 蒟蒻a&∀y(人y&食ya→太y) A
2 (3) 蒟蒻a 2&E
2 (4) ∀y(人y&食ya→太y) 2&E
2 (5) (人b&食ba→太b) 4UE
2 (6) ~(人b&食ba)∨太b 5含意の定義
7 (7) ~(人b&食ba) A
7 (8) (~人b∨~食ba) 7ド・モルガンの法則
7 (9) (~人b∨~食ba)∨太b 8∨I
ア(ア) 太b A
ア(イ) (~人b∨~食ba)∨太b ア∨I
2 (ウ) (~人b∨~食ba)∨太b 279アイ∨E
2 (エ) ~人b∨~食ba∨ 太b ウ結合法則
2 (オ) ~(人b&食ba&~太b) エ、ド・モルガンの法則
2 (カ) ∀y~(人y&食ya&~太y) オUI
2 (キ) ~∃y(人y&食ya&~太y) カ量化子の関係
2 (ク) 蒟蒻a&~∃y(人y&食ya&~太y) 3キ&I
2 (ケ) ~{~蒟蒻a∨∃y(人y&食ya&~太y)} ク、ド・モルガンの法則
2 (コ) ~{蒟蒻a→∃y(人y&食ya&~太y)} ケ含意の定義
2 (サ)∃x~{蒟蒻a→∃y(人y&食ya&~太y)} コEI
1 (シ)∃x~{蒟蒻a→∃y(人y&食ya&~太y)} 12サEE
1 (ス)~∀x{蒟蒻x→∃y(人y&食yx&~太y)} サ量化子の関係
従って、
(08)により、
(09)
② ~∀x{蒟蒻x→∃y(人y&食yx&~太y)}
③ ∃x{蒟蒻x&∀y(人y&食yx→ 太y)}
に於いて、
②=③ であるため、「両辺」を「否定」すると、「二重否定」により、
② ∀x{蒟蒻x→∃y(人y&食yx&~太y)}
③ ~∃x{蒟蒻x&∀y(人y&食yx→ 太y)}
に於いて、
②=③ である。
従って、
(05)(07)(09)により、
(10)
① 蒟蒻は、太らない。⇔
② ∀x{蒟蒻x→∃y(人y&食yx&~太y)}⇔
③ ~∃x{蒟蒻x&∀y(人y&食yx→ 太y)}⇔
④ 食べた人が太る所の「コンニャク」は存在しない。
といふ「日本語」に「相当」する『文型』が、「英語」には無いからと言って、
① 蒟蒻は、太らない。
④ 蒟蒻は、人、これを食して、太ること無し。
といふ「日本語」自体が、「非(述語)論理的な言い方」であるといふことには、ならない。
然るに、
(11)
日本語の文構造がどういうものなのかを説明するときに、問題になる例文がいくつかあります。たとえば「こんにゃく文」と呼ばれるものです。「こんにゃくは太りません」という例文には主語があるでしょうか。主語があるとしたら何であるかが問題になります。
(my コンテンツ工房|業務コンサルタント 丸山有彦)
然るに、
(03)(10)(11)により、
(12)
① 蒟蒻は、美味である。
② 蒟蒻は、太らない。
に於ける、
①「蒟蒻は」は、「主語」 であり、
②「蒟蒻は」は、「提示語」である。
然るに、
(13)
② 蒟蒻は、太らない。
③ 蒟蒻は、人、これを食して、太ること無し。
に於いて、
②=③ である。
といふことは、
③ 蒟蒻は、「提示語」であると「同時」に、「目的語」である。
といふことになる。
従って、
(13)により、
(14)
② 蒟蒻は、太らない。⇔
③ 蒟蒻は、人、これを食して、太ること無し。
に於ける、
②「蒟蒻は(提示語)」は、「主語」のやうであり、実質的には、「目的語」である。
(01)
よく知られているように、「私が理事長です」は語順を変え、
理事長は、私です。 と直して初めて主辞賓辞が適用されるのである。また、かりに大倉氏が、
タゴール記念会は、私が理事長です。
と言ったとすれば、これは主辞「タゴール記念会」を品評するという心持ちの文である。
(三上章、日本語の論理、1963年、40・41頁)
然るに、
(02)
1 (1)∀x{T会の会員x→∃y[私y&理事長yx&∀z(理事長zx→y=z)]} A
1 (2) T会の会員a→∃y[私y&理事長ya&∀z(理事長za→y=z)] 1UE
3 (3) T会の会員a A
13 (4) ∃y[私y&理事長ya&∀z(理事長za→y=z)] 23MPP
5 (5) 私b&理事長ba&∀z(理事長za→b=z) A
5 (6) 私b&理事長ba 5&E
5 (7) ∀z(理事長za→b=z) 5&E
5 (8) 理事長ca→b=c 7UE
9 (9) ∃z(大倉z&理事長za&~私z) A
ア (ア) 大倉c&理事長ca&~私c A
ア (イ) 大倉c ア&E
ア (ウ) ~私c ア&E
エ (エ) b=c A
アエ (オ) ~私b ウエ=E
5 (カ) 私b 6&E
5 アエ (キ) ~私b&私b オカ&I
5 ア (ク) b≠c エキRAA
5 ア (ケ) ~理事長ca 8クMTT
5 (コ) 理事長ca ア&E
5 ア (サ) 理事長ca&~理事長ca ケコ&I
59 (シ) 理事長ca&~理事長ca 9アサEE
5 (ス) ~∃z(大倉z&理事長za&~私z) 9シRAA
5 (セ) ∀z~(大倉z&理事長za&~私z) ス量化子の関係
5 (ソ) ~(大倉c&理事長ca&~私c) セUE
5 (タ) ~大倉c∨~理事長ca∨ 私c ソ、ド・モルガンの法則
5 (チ) (~大倉c∨~理事長ca)∨私c タ結合法則
ツ (ツ) (~大倉c∨~理事長ca) A
ツ (テ) ~(大倉c& 理事長ca) ツ、ド・モルガンの法則
ツ (ト) ~(大倉c& 理事長ca)∨私c テ∨I
ナ (ナ) 私c A
ナ (ニ) ~(大倉c& 理事長ca)∨私c ナ∨I
5 (ヌ) ~(大倉c& 理事長ca)∨私c チツトナニ∨E
5 (ネ) (大倉c& 理事長ca)→私c ヌ含意の定義
ノ (ノ)∀x{T会の会員x→∃z(大倉z&理事長zx)} A
ノ (ハ) T会の会員a→∃z(大倉z&理事長za) ノUE
3 ノ (ヒ) ∃z(大倉z&理事長za) 3ハMPP
フ(フ) 大倉c&理事長ca A
35 フ(ヘ) 私c ネフMPP
35 フ(ホ) 私c&大倉c&理事長ca フヘ&I
35 フ(マ) ∃z(私z&大倉z&理事長za) ホEI
35 ノ (ミ) ∃z(私z&大倉z&理事長za) ヒフマEE
1 ノ (メ) T会の会員a→∃z(私z&大倉z&理事長za) 3ムCP
1 ノ (モ)∀x{T会の会員x→∃z(私z&大倉z&理事長zx)} ノUI
従って、
(02)により、
(03)
(ⅰ)∀x{T会の会員x→∃y[私y&理事長yx&∀z(理事長zx→y=z)]}。然るに、
(ⅱ)∀x{T会の会員x→∃z(大倉z& 理事長zx)}。 従って、
(ⅲ)∀x{T会の会員x→∃z(私z&大倉z&理事長zx)}。
といふ「推論」、すなはち、
(ⅰ)すべてのxについて{xがタゴール記念会の会員であるならば、あるyは[私であって、理事長であって、すべてのzについて(zがxの理事長であるならば、y=zである)]}。然るに、
(ⅱ)すべてのxについて{xがタゴール記念会の会員であるならば、あるzは( 大倉であって、zはxの理事長である)}。従って、
(ⅲ)すべてのxについて{xがタゴール記念会の会員であるならば、あるzは(私であって、大倉であって、zはxの理事長である)}。
といふ「推論」、すなはち、
(ⅰ)タゴール記念会は、 私が理事長です。然るに、
(ⅱ)タゴール記念会は、 大倉は理事長です。従って、
(ⅲ)タゴール記念会は、私、大倉が理事長です。
といふ「推論」は、「妥当」である。
然るに、
(04)
① タゴール記念会(の会員)は、私が理事長です。
② 太陽系(の天体)は、地球が、第三惑星である。
といふ「日本語」は、『同じ構造』をしてゐるため、両方とも、
① ∀x{T会の会員x →∃y[ 私y& 理事長yx&∀z( 理事長zx→y=z)]}。
② ∀x{太陽系の天体x→∃y[地球y&第三惑星yx&∀z(第三惑星zx→y=z)]}。
といふ風に、書くことが出来る。
然るに、
(05)
1 (1)∀x{太陽系x→∃y[地球y&第三惑星yx&∀z(第三惑星zx→y=z)]} A
1 (2) 太陽系a→∃y[地球y&第三惑星ya&∀z(第三惑星za→y=z)] 1UE
3 (3) 太陽系a A
13 (4) ∃y[地球y&第三惑星ya&∀z(第三惑星za→y=z)] 23MPP
5 (5) 地球b&第三惑星ba&∀z(第三惑星za→b=z) A
5 (6) 地球b&第三惑星ba 5&E
5 (7) ∀z(第三惑星za→b=z) 5&E
5 (8) 第三惑星ca→b=c 7UE
9 (9) ∃z(火星z&~地球z) A
ア (ア) 火星c&~地球c A
ア (イ) 火星c ア&E
ア (ウ) ~地球c ア&E
エ(エ) b=c A
アエ(オ) ~地球b ウエ=E
5 (カ) 地球b 6&E
5 アエ(キ) ~地球b&地球b オカ&I
5 ア (ク) b≠c エキRAA
5 ア (ケ) ~第三惑星ca 8クMTT
5 ア (コ) 火星c&~第三惑星ca イケ&I
5 ア (サ) ∃z(火星z&~第三惑星za) コEI
59 (シ) ∃z(火星z&~第三惑星za) 9アサEE
13 9 (ス) ∃z(火星z&~第三惑星za) 45シEE
1 9 (セ) 太陽系a→∃z(火星z&~第三惑星za) 3スCP
1 9 (ソ)∀x{太陽系x→∃z(火星z&~第三惑星zx)} セUI
従って、
(05)により、
(06)
(ⅰ)太陽系は、地球が第三惑星である。然るに、
(ⅱ)火星は、 地球ではない。 従って、
(ⅲ)太陽系は、火星は第三惑星ではない。
といふ「推論」は、「妥当」である。
然るに、
(07)
① 太陽系は、地球が第三惑星である。
② 太陽系は、銀河系である。
に対して、
① ∀x{太陽系x→∃y[地球y&第三惑星yx&∀z(第三惑星zx→y=z)]}。
② ∀x{太陽系x→銀河系x}。
従って、
(08)
① 太陽系は、地球が第三惑星である。
② 太陽系は、銀河系である。
に於ける、
① 太陽系は、
② 太陽系は、
は、両方とも、
① ∀x{太陽系x→
② ∀x{太陽系x→
であって、「区別」が無い。
然るに、
(09)
① 太陽系は、地球が第三惑星である。
② 太陽系は、銀河系である。
に対する、「グーグル翻訳」は、
① In the solar system, the earth is the third planet.
② The solar system is a galaxy.
然るに、
(10)
① In the solar system, the earth is the third planet.
といふ「英語」は、
① 太陽系は、地球が第三惑星である。
といふ風に、『訳してから』でないと、
① ∀x{太陽系x→∃y[地球y&第三惑星yx&∀z(第三惑星zx→y=z)]}。
といふ風に、「翻訳出来ない」。
従って、
(09)(10)により、
(11)
① 太陽系は、地球が第三惑星である。⇔
① In the solar system, the earth is the third planet.⇔
① ∀x{太陽系x→∃y[地球y&第三惑星yx&∀z(第三惑星zx→y=z)]}。
で「比較」する限り、「非(述語)論理的な言語」は、「日本語」ではなく、むしろ「英語」である。
cf.
一、總主トハ如何ナル者ゾ
動詞、形容詞ニ對シテ其主語アルト同ジク、主語ト説語(動詞或ハ形容詞)トヨリ成レル一ノ説話(即チ文)ニ對シテモ更ニソノ主語アルコト國語ニハ屡々アリ。例ヘバ「象は體大なり」ノ「象」、「熊は力強し」ノ「熊」、「鳥獸蟲魚皆性あり」ノ「鳥獸蟲魚」、「仁者は命長し」ノ「仁者」、「賣藥は效能薄し」ノ「賣藥」、「慾は限無し」ノ「慾」、「酒は養生に害あり」ノ「酒」、「支那は人口多し」ノ「支那」ノ如キハ、皆、「體大なり」「力強し」等ノ一説話ニ對シテ更ニソノ主語タル性格ヲ有ス。何トナレバ「象は體大なり」「熊は力強し」等ヨリ「象」「熊」等ノ再度ノ主語ヲ取去ル時ハ、殘餘ハ「體大なり」「力強し」等トナリテ、文法上ノ文ノ形ハ完全ニ之ヲ具フルニモ拘ラズ、意義ニ不足ヲ生ジ、其事ノ主トアルベキ「象」「熊」等ノ名詞ヲ竢ッテ始メテ意義ノ完全ナル一圓ノ説話ヲ成サントスル傾アルコト、ナホ普通ノ動詞、形容詞ノ名詞ヲ竢ッテ始メテ一ノ完全ナル説話ヲ成サントスル傾アルト同趣味ノモノアレバナリ。殊ニ「性有り」「限無し」等ノ一種ノ説話ニ對シテハ、實用ノ際ニ再度ノ主語ノ必要アル事ハ頗ル顯著ナルニアラズヤ。コレハ「うら(心)やまし(疚)」「て(質)がたし(堅)」ナドノ一説話ノ轉シテ一ノ形容詞トナリ、然ル上ハ實用ノ際ニ更ニソノ主語ヲ取ルト一般ナリ。サレバ「富貴は羨し」ノ「うらやまし」ニ對シテ「富貴」ヲ主語トイフヲ至當トセバ、「體大なり」「力強し」ニ對シテ「象」「熊」ヲソノ主語トイフモ亦不當ニハアラジ。斯カレバコノ類ノ再度ノ主ヲ予ハ別ニ「總主」ト名ヅケントス。
總主ハ斯ク頗ル簡單ニ説明セラルベク、亦容易ニ會得セラルベキ者ナリ。學者ノ潛思苦慮ヲモ要セズ、考古引證ヲモ須タズシテ、小學ノ兒童モ、口頭ニ、文章ニ、此語法ヲ用ヰ、歌人文士モ之ヲ用ヰテ毫モ疑フ事ナシ。コノ語法ハ本ヨリ我國ニ有リシナランガ、漢學ノ流行ニ連レテ益廣ク行ハレ、今日トナリテハ最早之ヲ目シテ國語ノ法則ニ非ズトイフヲ得ザルニ至レリ。然ルニ國語ノ法則トシテ日本ノ文法ニ之ヲ編入スル者ナキハ何故ゾ。西洋ノ言語ニ類似ノ語法ナク、西洋ノ文典ニ類似ノ記載ナキガ故ニハ非ザルカ。
(草野淸民、國語の特有セル語法 ― 總主、『帝國文學』五卷五號、明治三十二年:大修館書店、日本の言語学 第3巻 文法Ⅰ、1978年、533頁)
(01)
「マイクロソフトのBingAI」に、
太郎というのは、男子の名前ですか。
といふ風に、質問したところ、
はい、太郎というのは男子の名前です。1 一般的には長男の名前であり、次男は「二郎」、三男は「三郎」と続くことが多いです。
とのことである。
従って、
(01)により、
(02)
「太郎は男子で、花子は女子である。」
と言ふのであれば、「普通」である。
従って、
(02)により、
(03)
「太郎は男子で、花子は女子である。」
と言ふのではなく、
「花子は男子で、太郎は女子である。」
と言ふのであれば、「普通」ではない。
然るに、
(04)
「花子は男子で、太郎は女子である。」
といふのであれば、「私がそれを言ふ」のであれば、「誤解」を避けるために、
「花子が男子で、太郎が女子です。」
と言ふことになり、その場合は、
「(太郎ではなく)花子が男子で、(花子ではなく)太郎が女子です。」
といふ「意味」になる。
従って、
(04)により、
(05)
「花子が男子で、太郎が女子です。」
といふ「日本語」は、
「(他ならぬ)花子が男子で、(他ならぬ)太郎が女子です。」
といふ「意味」になる。
従って、
(06)
「おばあさんは山へしば刈りに、おじいさんは川へ洗濯に行きました。」
とは言わずに、
「おばあさんが山へしば刈りに、おじいさんが川へ洗濯に行きました。」
と言ふのであれば、
「(おじいさんではなく)おばあさんが山へしば刈りに、(おばあさんではなく)おじいさんが川へ洗濯に行きました。」
といふことで、
「(他ならぬ)おばあさんが山へしば刈りに、(他ならぬ)おじいさんが川へ洗濯に行きました。」
といふ「意味」になる。
(07)
「むかし、むかし、ある所におじいさんとおばあさんが住んでいました。」
といふのは、
「むかし、むかし、ある所におじいさんとおばあさんだけが住んでいました(、この時はまだ、桃太郎はいませんでした)。」
といふ「意味」である。
(01)
「ラテン語のbe動詞」は、
① sum(私は、 ・・・である)。
② es(汝は、 ・・・である)。
③ est(彼は、 ・・・である)。
④ sumus(我らは、・・・である)。
⑤ estis(汝らは、・・・である)。
⑥ sunt(彼らは、・・・である)。
従って、
(01)により、
(02)
① sum 理事長(私は、 理事長である)。
② es 理事長(汝は、 理事長である)。
③ est 理事長(彼は、 理事長である)。
④ sumus 理事長(我らは、 理事長である)。
⑤ estis 理事長(汝らは、 理事長である)。
⑥ sunt 理事長(彼らは、 理事長である)。
然るに、
(03)
人称代名詞が主語としてつかわれることは、意を強める場合か、対照的の場合ほかはないといっていい。
これは普通主語は動詞の語尾で表せていて、すぐわかるからである。
Ego te laudo,tu me non laudas.
ここで ego(私が)といい、tu(お前が)というのは、特に「自分だ、と誉めるのは自分だ」と強調したからであり、また、一方 ego 一方 tu と対象させたからである。
(村松正俊、ラテン語四週間、1951年、182頁)
従って、
(02)(03)により、
(04)
① Sum(一人称・単数) 理事長。
と言はずに、わざわざ、
② Ego(一人称・単数) sum(一人称・単数) 理事長。
といふのであれば、
② 主語(一人称・単数)
が、「強調」され、その「結果」として、
② 私は理事長であり、私以外は理事長ではない。
といふ、「意味」になる。
然るに、
(05)
私が理事長です(理事長は私です)。
のように、ガの文はハを内蔵していることがあるから、その説明が必要である。
このような「私が」を強制的になっていると言うことにする。そこには発音上のストレスを与えたのと似た効果をもっているからである。
(三上章、日本語の論理、1963年、105頁)
然るに、
(06)
清音の方は、小さくきれいで速い感じで、コロコロと言うと、ハスの上を水玉がころがるような時の形容である。ゴロゴロと言うと、大きく荒い感じで、力士が土俵でころがる感じである(金田一春彦、日本語(上)、1988年、131頁)。もし濁音を発音するときの物理的・身体的な口腔の膨張によって「濁音=大きい」とイメージがつくられているのだとしたら、面白いですね。この仮説が正しいとすると、なぜ英語話者や中国語話者も濁音に対して「大きい」というイメージを持っているか説明がつきます(川原繁人、音とことばの不思議な世界、2015年、13頁)。
従って、
(05)(06)により、
(07)
① 私は(清音)
よりも、
② 私が(濁音)
の方が、「心理的な音量」が「大きい」。
といふ「意味」に於いて、
① 私は(清音)
に対する、
② 私が(濁音)
は、「強調形」である。
従って、
(04)~(07)により、
(08)
① 私は(清音)理事長です。
と言はずに、敢へて、
② 私が(濁音)理事長です。
と言ふのであれば、その場合は、
② 私は理事長であり、私以外は理事長ではない。
といふ、「意味」になる。
然るに、
(09)
②「私」は、「私」だけであって、
②「私」以外に、「私」はゐない。
従って、
(09)により、
(10)
③ 理事長は私です。
といふのあれば、
② 私以外に理事長はゐない。
然るに、
(11)
よく知られているように、「私が理事長です」は語順を変え、
理事長は、私です。 と直して初めて主辞賓辞が適用されるのである。また、かりに大倉氏が、
タゴール記念会は、私が理事長です。
と言ったとすれば、これは主辞「タゴール記念会」を品評するという心持ちの文である。
(三上章、日本語の論理、1963年、40・41頁)
従って、
(10)(11)により、
(12)
① 私が理事長です。
② 私以外に理事長はゐない。
③ 理事長は私です。
に於いて、
①=②=③ である。
然るに、
(13)
1 (1)∀x{T会の会員x→∃y[私y&理事長yx&∀z(理事長zx→y=z)]} A
1 (2) T会の会員a→∃y[私y&理事長ya&∀z(理事長za→y=z)] 1UE
3 (3) T会の会員a A
13 (4) ∃y[私y&理事長ya&∀z(理事長za→y=z)] 23MPP
5 (5) 私b&理事長ba&∀z(理事長za→b=z) A
5 (6) 私b&理事長ba 5&E
5 (7) ∀z(理事長za→b=z) 5&E
5 (8) 理事長ca→b=c 7UE
9 (9) ∃z(小倉z&~私z) A
ア (ア) 小倉c&~私c A
ア (イ) 小倉c ア&E
ア (ウ) ~私c ア&E
エ(エ) b=c A
アエ(オ) ~私b ウエ=E
5 (カ) 私b 6&E
5 アエ(キ) ~私b&私b オカ&I
5 ア (ク) b≠c エキRAA
5 ア (ケ) ~理事長ca 8クMTT
5 ア (コ) 小倉c&~理事長ca イケ&I
5 ア (サ) ∃z(小倉z&~理事長za) コEI
59 (シ) ∃z(小倉z&~理事長za) 9アサEE
13 9 (ス) ∃z(小倉z&~理事長za) 45シEE
1 9 (セ) T会の会員a→∃z(小倉z&~理事長za) 3スCP
1 9 (ソ)∀x{T会の会員x→∃z(小倉z&~理事長zx)} セUI
従って、
(13)により、
(14)
(ⅰ)∀x{T会の会員x→∃y[私y&理事長yx&∀z(理事長zx→y=z)]}。然るに、
(ⅱ)∃z(小倉z&~私z)。従って、
(ⅲ)∀x{T会の会員x→∃z(小倉z&~理事長zx)}。
といふ「推論」、すなはち、
(ⅰ)すべてのxについて{xがタゴール記念会の会員であるならば、あるyは[私であって、理事長であって、すべてのzについて(zがxの理事長であるならば、y=zである)]}。然るに、
(ⅱ)あるzは(小倉であって、私ではない)。従って、
(ⅲ)すべてのxについて{xがタゴール記念会の会員であるならば、あるzは(小倉であって、小倉はxの理事長ではない)}。
といふ「推論」、すなはち、
(ⅰ)タゴール記念会は、私が理事長です。然るに、
(ⅱ)小倉氏は私ではない。従って、
(ⅲ)タゴール記念会は、小倉氏は理事長ではない。
といふ「推論」は、「妥当」である。
従って、
(12)(13)(14)により、
(15)
① タゴール記念会は、私が理事長です。
② タゴール記念会は、私以外に理事長はゐない。
③ タゴール記念会は、理事長は私です。
④ ∀x{T会の会員x→∃y[私y&理事長yx&∀z(理事長zx→y=z)]}。
に於いて、
①=②=③=④ である。
然るに、
(16)
① 象は動物である。
② 象といふ「集合」は、「動物」といふ「集合の(真)部分集合」である。
③ ∀x(象x→動物x)。
に於いて、
①=②=③ であって、尚且つ、
①「象は」は、「動物である」といふ「述語」の「主語」である。
然るに、
(17)
① タゴール記念会は、私が理事長です。
④ ∀x{T会の会員x→∃y[私y&理事長yx&∀z(理事長zx→y=z)]}。
に於いて、
④ タゴール記念会の会員 といふ「集合」は、「私が理事長です」といふ「集合(?)の部分集合」である。
といふわけではない。
然るに、
(16)(17)により、
(18)
③ ∀x(象x→
④ ∀x{T会の会員x→
は、両方とも、
③ ∀x(Fx→
④ ∀x(Fx→
といふ「形」、
③ すべてのxについて、xがFならば、
④ すべてのxについて、xがFならば、
といふ「形」をしてゐる。
従って、
(16)(17)(18)により、
(19)
③ ∀x(Fx→
④ ∀x(Fx→
といふ「意味」である所の、
③ Fは
④ Fは
は、「主語」である。
とするならば、
③ 象は
④ タゴール記念会は
は、両方とも、「主語」である。
因みに、
(20)
「Bing AI」に「質問」をしたところ、
「象は鼻が長い」の「主語」は、「象」であり、
「象は鼻が長い」の「述語」は、「鼻が長い」であり、
三上文法では、日本語の主語は「主格が或る特別なはたらきをする国語において、その主格に認められる資格」とされています。しかし、三上のような「主語」概念とは異なる、認識論的(或いは存在論的)な「主語」了解の仕方もあり得て、そうした「主語」了解に立てば、日本語にも主語はあるということになります1。
一般的な日本語の主語と三上文法の主格が異なる点は、三上文法では、主格が或る特別なはたらきをする国語において、その主格に認められる資格を持つものが「主語」とされている点です1。
との、ことである。
然るに、
(21)
「ラテン語」等でいふ、
「主格」といふのは、「文の中の、その名詞・形容詞が、述語に対する、主語であることを」を示すための「語形」であるため、
「主格が或る特別なはたらきをする国語において、」といふのであれば、
「日本語」では、「主語を示すための語形」が「或る特別なはたらきをする」といふことなる(?!?!?)。
然るに、
(22)
漢文におけるこのような表現のしかたは、単語の間の関係を文法的な形式によって示すことを重んじている(ラテン語のような)西欧の言語になれている人にとっては、まことに奇妙なことに思われるものと考えられる。カールグレン氏は、その著書《中国の言語》において、このような奇妙な孤立的な漢語の文法は、「非常に貧弱なものであり」、「漢語においては、文法的な分析は、あまり役に立たず、実際に役立つのは、広い読書を通じて習得した経験、つまり、中国人がどのようにして文をつくりあげているかということに対する感覚が、唯一のものである」と説き、更に、漢文の文の意味を理解するためには、「豊富な直観が、必要である」とも述べている(鈴木直治著、中国語と漢文、1975年、293頁改)。
従って、
(22)により、
(23)
例へば、「漢文」の場合は、「主語」は有ったとしても、「主格(といふ語形)」は、無いことなるし、そのため、
けだし、「主格」の無い「言語」は有り得ても、「主語」の無い「言語」は、有り得ないはずである。
(24)
「ラテン語やギリシャ語の文法でいう、主格や属格というのは、語形のことですか。」
といふ風に、「Bing AI」に「質問」をしたところ、
「はい、主格や属格というのは、名詞や代名詞などの語形のことを指します。」
とのことである。
―「昨日(令和5年6月3日)の記事」を書き直します。―
(01)
1 (1)∀x{犯人x→(x=佐藤)∨(x=鈴木) ∨(x=高橋)} A
2 (2)∀x(犯人x→~アリバイx) A
3 (3)アリバイ高橋&アリバイ鈴木 A
1 (4) 犯人a→(a=佐藤)∨(a=鈴木) ∨(a=高橋) 1UE
2 (5) 犯人a→~アリバイa 2UE
6 (6) 犯人a A
2 6 (7) ~アリバイa 56MPP
8 (8) 高橋=a A
9 (9) 鈴木=a A
2 68 (ア) ~アリバイ高橋 78=E
2 6 9 (イ) ~アリバイ鈴木 79=E
3 (ウ)アリバイ高橋 3&E
3 (エ)アリバイ鈴木 3&E
2368 (オ)アリバイ高橋&~アリバイ高橋 アウ&I
236 9 (カ)アリバイ鈴木&~アリバイ鈴木 イエ&I
236 (キ) 高橋≠a 8オRAA
236 (ク) 鈴木≠a 9カRAA
1 6 (ケ) (a=佐藤)∨(a=鈴木) ∨(a=高橋) 46MPP
1 6 (コ) {(a=佐藤)∨(a=鈴木)}∨(a=高橋) ケ結合法則
サ (サ) {(a=佐藤)∨(a=鈴木)} A
サ (シ) ~~{(a=佐藤)∨(a=鈴木)} サDN
サ (ス) ~{(a≠佐藤)&(a≠鈴木)} シ、ド・モルガンの法則
サ (セ) ~{(a≠佐藤)&(a≠鈴木)}∨(a=高橋) ス∨I
ソ (ソ) (a=高橋) A
ソ (タ) ~{(a≠佐藤)&(a≠鈴木)}∨(a=高橋) ソ∨I
1 6 (チ) ~{(a≠佐藤)&(a≠鈴木)}∨(a=高橋) コサセソタ∨E
1 6 (ツ) {(a≠佐藤)&(a≠鈴木)}→(a=高橋) チ含意の定義
1236 (テ) ~{(a≠佐藤)&(a≠鈴木)} キツMTT
1236 (ト) ~(a≠佐藤)∨(a=鈴木) テ、ド・モルガンの法則
1236 (ナ) (a≠佐藤)→(a=鈴木) ト、含意の定義
1236 (ニ) (a=佐藤) クナMTT
123 (ヌ) 犯人a→(a=佐藤) 6ニCP
ネ(ネ) (a≠佐藤) A
123 ネ(ノ) ~犯人a ヌネMTT
123 (ハ) (a≠佐藤)→~犯人a ネノCP
123 (ヒ) 犯人a→(a=佐藤)&(a≠佐藤)→~犯人a ナニヒ&I
123 (フ)∀x{犯人x→(x=佐藤)&(x≠佐藤)→~犯人x} ヒUI
従って、
(01)により、
(02)
(ⅰ)∀x{犯人x→(x=佐藤)∨(x=鈴木)∨(x=高橋)}。然るに、
(ⅱ)∀x(犯人x→~アリバイx)。然るに、
(ⅲ)アリバイ高橋&アリバイ鈴木。従って、
(ⅳ)∀x{(犯人x→x=佐藤)&(x≠佐藤→~犯人x)}。
といふ「推論」、すなはち、
(ⅰ)すべてのxについて{xが犯人であるならば、(xは佐藤である)か、(xは鈴木である)か、(xは高橋である)}。然るに、
(ⅱ)すべてのxについて(xが犯人であるならば、xにはアリバイが無い)。然るに、
(ⅲ)高橋にはアリバイがあるし、鈴木にもアリバイがある。従って、
(ⅳ)すべてのxについて{(xが犯人であるならば、xは佐藤であり)、尚且つ(xが佐藤でなければ、xは犯人ではない)}。
といふ「推論」は、「述語論理(古典論理)」として、「妥当」である。
従って、
(02)により、
(03)
(ⅰ)犯人は、佐藤か、鈴木か、高橋である。然るに、
(ⅱ)犯人であれば、 アリバイが無い。然るに、
(ⅲ)高橋と鈴木には、アリバイが有る。従って、
(ⅳ)犯人は佐藤であり、佐藤以外(高橋と鈴木)は犯人ではない。
といふ「推論」は、「述語論理(数学語)」だけでなく、「日本語」としても、「妥当」である。
従って、
(03)により、
(04)
② 犯人は佐藤である。
③ 佐藤以外は犯人ではない。
に於いて、
②=③ である。
然るに、
(05)
Q:誰が犯人か。
A:佐藤が犯人である。
であって、
Q:誰は犯人か。
A:佐藤は犯人である。
ではない。
従って、
(04)(05)により、
(06)
① 佐藤が犯人である。
② 犯人は佐藤である。
③ 佐藤以外は犯人ではない。
に於いて、
①=②=③ である。
然るに、
(07)
よく知られているように、「私が理事長です」は語順を変え、
理事長は、私です。 と直して初めて主辞賓辞が適用されるのである。また、かりに大倉氏が、
タゴール記念会は、私が理事長です。
と言ったとすれば、これは主辞「タゴール記念会」を品評するという心持ちの文である。
(三上章、日本語の論理、1963年、40・41頁)
従って、
(06)(07)により、
(08)
① 私が理事長である。
② 理事長は私である。
③ 私以外は理事長ではない。
に於いて、
①=②=③ である。
然るに、
(09)
私が理事長です(理事長は私です)。
のように、ガの文はハを内蔵していることがあるから、その説明が必要である。
このような「私が」を強制的になっていると言うことにする。そこには発音上のストレスを与えたのと似た効果をもっているからである。
(三上章、日本語の論理、1963年、105頁)
然るに、
(10)
清音の方は、小さくきれいで速い感じで、コロコロと言うと、ハスの上を水玉がころがるような時の形容である。ゴロゴロと言うと、大きく荒い感じで、力士が土俵でころがる感じである(金田一春彦、日本語(上)、1988年、131頁)。もし濁音を発音するときの物理的・身体的な口腔の膨張によって「濁音=大きい」とイメージがつくられているのだとしたら、面白いですね。この仮説が正しいとすると、なぜ英語話者や中国語話者も濁音に対して「大きい」というイメージを持っているか説明がつきます(川原繁人、音とことばの不思議な世界、2015年、13頁)。
従って、
(08)(09)(10)により、
(11)
① 私が理事長である。
② 理事長は私である。
③ 私以外は理事長ではない。
に於いて、
①=②=③ であって、尚且つ、
①「私が(濁音)」は、「濁音」による「強調形」である。
然るに、
(12)
エゴー・エイミ(古代ギリシャ語: ἐγώ εἰμι ギリシャ語の発音: [eɡɔ̌ː eːmí] ) 「私はいる」、「私は存在する」は、古代ギリシャ語の動詞「である」を示す一人称単数 現在 能 動詞です(ウィキペディア)。
(13)
(a)この理由は、動詞の語尾が、主語が一人称であるか、それとも二人称であるか、または、三人称であるかを充分に示しているからである。つまり λεγω は「私は言う」(I say)である。故に、特に「私」を強調が置かれるのでなければ、εγω を付け加えない。
(b)強調というのは、通常対照によって生ずる。たとえば、εγω λεγω,συ δε γραφειs,「私は語るが、しかし汝は書く」(I say,but you write)という文で,εγω と συ とは強調されている。εγω と συ は互いに対照されているからである。そして、εγω λεγω、「私は語る」(I say)という文では、誰か他の人は語っていないということが、当然、類推されるわけである。
(J.G.メイチェン著、田辺滋 訳、新約聖書ギリシャ語原点入門、1967年、55頁)
従って、
(11)(12)(13)により、
(14)
① 私が理事長である。
② εγω・ειμι the 理事長。
③ 私以外は理事長ではない。
に於いて、
①=②=③ であって、尚且つ、
①「私が(濁音)」は、「濁音」による「強調形」であって、
②「εγω+一人称動詞」は、「一人称代名詞・主格」による「強調形」である。
然るに、
(15)
③ 私以外は理事長ではない。
のやうな「命題」を、「排他的命題(Exclusive propsition)」といふ。
従って、
(14)(15)により、
(16)
① 私が理事長である。
② εγω・ειμι the 理事長。
は、両方とも、「強調形」であって、尚且つ、「排他的命題」である。