（01）
『ユウチューブ』を視聴して、「説明」を聞いても『納得できない』ので、
［問題］
女子２人と男子３が１列に並ぶとき、
女子が隣り合わない並び方は「何通り」作れるか（有り得るか）。
という［問題］を、自分自身で、「考察」することにした。
（02）
（ⅰ）
１男２男３男４
という「列」に於いて、
女子Ａが、１に入ったら、
女子Ｂは、２か、３か、４に入る。
ということを、
①１・２
②１・３
③１・４
という風に、表すことにする。
（ⅱ）
１男２男３男４
という「列」に於いて、
女子Ａが、２に入ったら、
女子Ｂは、１か、３か、４に入る。
ということを、
④２・１
⑤２・３
⑥２・４
という風に、表すことにする。
（ⅲ）
１男２男３男４
という「列」に於いて、
女子Ａが、３に入ったら、
女子Ｂは、１か、２か、４に入る。
ということを、
⑦３・１
⑧３・２
⑨３・４
という風に、表すことにする。
（ⅳ）
１男２男３男４
という「列」に於いて、
女子Ａが、４に入ったら、
女子Ｂは、１か、２か、３に入る。
ということを、
⑩４・１
⑪４・２
⑫４・３
という風に、表すことにする。
然るに、
（03）
①１・２⇒Ａ男Ｂ男３男４
②１・３⇒Ａ男２男Ｂ男４
③１・４⇒Ａ男２男３男Ｂ
④２・１⇒Ｂ男Ａ男３男４
⑤２・３⇒１男Ａ男Ｂ男４
⑥２・４⇒１男Ａ男３男Ｂ
⑦３・１⇒Ｂ男２男Ａ男４
⑧３・２⇒１男Ｂ男Ａ男４
⑨３・４⇒１男２男Ａ男Ｂ
⑩４・１⇒Ｂ男２男３男Ａ
⑪４・２⇒１男Ｂ男３男Ａ
⑫４・３⇒１男２男Ｂ男Ａ
という「順番」は、
④２・１⇒Ｂ男Ａ男３男４
⑦３・１⇒Ｂ男２男Ａ男４
⑩４・１⇒Ｂ男２男３男Ａ
①１・２⇒Ａ男Ｂ男３男４
⑧３・２⇒１男Ｂ男Ａ男４
⑪４・２⇒１男Ｂ男３男Ａ
②１・３⇒Ａ男２男Ｂ男４
⑤２・３⇒１男Ａ男Ｂ男４
⑫４・３⇒１男２男Ｂ男Ａ
③１・４⇒Ａ男２男３男Ｂ
⑥２・４⇒１男Ａ男３男Ｂ
⑨３・４⇒１男２男Ａ男Ｂ
という風に、「並び変える」ことが、出来る。
従って、
（02）（03）により、
（04）
例えば、
（ⅰ）
１男２男３男４
という「列」に於いて、
女子Ａが、１に入ったら、
女子Ｂは、２か、３か、４に入る。
という風に「数える」ことは、それと「同時」に、
（ⅰ）
１男２男３男４
という「列」に於いて、
女子Ｂが、１に入ったら、
女子Ａは、２か、３か、４に入る。
という風に「数える」ことに、「等しい」。
従って、
（02）（03）（04）により、
（05）
１男２男３男４
女子Ａが、１に入ったら、
に対して、
１男２男３男４
女子Ｂが、１に入ったら、
ということを、「区別」して「数える」のであれば、その場合は、
「１回数えれば」で良いところを、「２回数えて」いることになる。
従って、
（02）～（06）により、
（07）
①１・２⇒Ａ男Ｂ男３男４
②１・３⇒Ａ男２男Ｂ男４
③１・４⇒Ａ男２男３男Ｂ
④２・１⇒Ｂ男Ａ男３男４
⑤２・３⇒１男Ａ男Ｂ男４
⑥２・４⇒１男Ａ男３男Ｂ
⑦３・１⇒Ｂ男２男Ａ男４
⑧３・２⇒１男Ｂ男Ａ男４
⑨３・４⇒１男２男Ａ男Ｂ
⑩４・１⇒Ｂ男２男３男Ａ
⑪４・２⇒１男Ｂ男３男Ａ
⑫４・３⇒１男２男Ｂ男Ａ
に於ける、
「（４×３＝１２）通リ」という「場合の数」は、
１男２男３男４
に於ける、
１ ２ ３ ４
の「位置」に、
女子Ａと、
女子Ｂが入る場合の、「場合の数」である。
然るに、
（08）
１男２男３男４
に於ける
男 男 男
が並ぶ場合の「場合の数」は、
（３！＝３×２×１）通りである。
従って、
（01）（07）（08）により、
（09）
［問題］
女子２人（Ａ、Ｂ）と男子３人（Ｃ、Ｄ、Ｅ）が１列に並ぶとき、
女子が隣り合わない「並び方」は「何通り」作れるか（有り得るか）。
の「答え」は、
（４×３）×（３×２×１）＝１２×６＝７２通り。
であるに、違いない。
然るに、
（10）
①ＡＢＣＤＥ
①ＡＢＣＥＤ
①ＡＢＤＣＥ
①ＡＢＤＥＣ
①ＡＢＥＣＤ
①ＡＢＥＤＣ
②ＡＣＢＤＥ
②ＡＣＢＥＤ
②ＡＣＤＢＥ
②ＡＣＤＥＢ
②ＡＣＥＢＤ
②ＡＣＥＤＢ
③ＡＤＢＣＥ
③ＡＤＢＥＣ
③ＡＤＣＢＥ
③ＡＤＣＥＢ
③ＡＤＥＢＣ
③ＡＤＥＣＢ
④ＡＥＢＣＤ
④ＡＥＢＤＣ
④ＡＥＣＢＤ
④ＡＥＣＤＢ
④ＡＥＤＢＣ
④ＡＥＤＣＢ
以上で、１８通り。
①ＢＡＣＤＥ
①ＢＡＣＥＤ
①ＢＡＤＣＥ
①ＢＡＤＥＣ
①ＢＡＥＣＤ
①ＢＡＥＤＣ
②ＢＣＡＤＥ
②ＢＣＡＥＤ
②ＢＣＤＡＥ
②ＢＣＤＥＡ
②ＢＣＥＡＤ
②ＢＣＥＤＡ
③ＢＤＡＣＥ
③ＢＤＡＥＣ
③ＢＤＣＡＥ
③ＢＤＣＥＡ
③ＢＤＥＡＣ
③ＢＤＥＣＡ
④ＢＥＡＣＤ
④ＢＥＡＤＣ
④ＢＥＣＡＤ
④ＢＥＣＤＡ
④ＢＥＤＡＣ
④ＢＥＤＣＡ
以上で、１８＋１８＝３６通り。
①ＣＡＢＤＥ
①ＣＡＢＥＤ
①ＣＡＤＢＥ
①ＣＡＤＥＢ
①ＣＡＥＢＤ
①ＣＡＥＤＢ
②ＣＢＡＤＥ
②ＣＢＡＥＤ
②ＣＢＤＡＥ
②ＣＢＤＥＡ
②ＣＢＥＡＤ
②ＣＢＥＤＡ
③ＣＤＡＢＥ
③ＣＤＡＥＢ
③ＣＤＢＡＥ
③ＣＤＢＥＡ
③ＣＤＥＡＢ
③ＣＤＥＢＡ
④ＣＥＡＢＤ
④ＣＥＡＤＢ
④ＣＥＢＡＤ
④ＣＥＢＤＡ
④ＣＥＤＡＢ
④ＣＥＤＢＡ
以上で、１８＋１８＋１２＝４８通り。
①ＤＡＢＣＥ
①ＤＡＢＥＣ
①ＤＡＣＢＥ
①ＤＡＣＥＢ
①ＤＡＥＢＣ
①ＤＡＥＣＢ
②ＤＢＡＣＥ
②ＤＢＡＥＣ
②ＤＢＣＡＥ
②ＤＢＣＥＡ
②ＤＢＥＡＣ
②ＤＢＥＣＡ
③ＤＣＡＢＥ
③ＤＣＡＥＢ
③ＤＣＢＡＥ
③ＤＣＢＥＡ
③ＤＣＥＡＢ
③ＤＣＥＢＡ
④ＤＥＡＢＣ
④ＤＥＡＣＢ
④ＤＥＢＡＣ
④ＤＥＢＣＡ
④ＤＥＣＡＢ
④ＤＥＣＢＡ
以上で、１８＋１８＋１２＋１２＝６０通り。
①ＥＡＢＣＤ
①ＥＡＢＤＣ
①ＥＡＣＢＤ
①ＥＡＣＤＢ
①ＥＡＤＢＣ
①ＥＡＤＣＢ
②ＥＢＡＣＤ
②ＥＢＡＤＣ
②ＥＢＣＡＤ
②ＥＢＣＤＡ
②ＥＢＤＡＣ
②ＥＢＤＣＡ
③ＥＣＡＢＤ
③ＥＣＡＤＢ
③ＥＣＢＡＤ
③ＥＣＢＤＡ
③ＥＣＤＡＢ
③ＥＣＤＢＡ
④ＥＤＡＢＣ
④ＥＤＡＣＢ
④ＥＤＢＡＣ
④ＥＤＢＣＡ
④ＥＤＣＡＢ
④ＥＤＣＢＡ
以上で、１８＋１８＋１２＋１２＋１２＝７２通り。
従って、
（09）（10）により、
（11）
［問題］
女子２人（Ａ、Ｂ）と男子３人（Ｃ、Ｄ、Ｅ）が１列に並ぶとき、
女子が隣り合わない「並び方」は「何通り」作れるか（有り得るか）。
の「答え」は、果たして、
（４×３）×（３×２×１）＝１２×６＝７２通り。
である。
然るに、
（12）
女子２人（Ａ、Ｂ）と男子３人（Ｃ、Ｄ、Ｅ）が１列に並ぶとき、
その「並び方」は、
５！＝５×４×３×２×１＝１２０通り。
である。
従って、
（11）（12）により、
（13）
女子２人（Ａ、Ｂ）と男子３人（Ｃ、Ｄ、Ｅ）が１列に並ぶとき、
女子が隣り合う「並び方」は「何通り」作れるか（有り得るか）。
の「答え」は、
（１２０－７２）＝４８通り。
である。
従って、
（01）～（13）により、
（14）
１男２男３男４
に於ける、
１の位置で、女子２人（Ａ、Ｂ）が隣り合い、
２の位置で、女子２人（Ａ、Ｂ）が隣り合い、
３の位置で、女子２人（Ａ、Ｂ）が隣り合い、
４の位置で、女子２人（Ａ、Ｂ）が隣り合う場合の、「合計の数」が、
（１２０－７２）＝１２＋１２＋１２＋１２＝４８通り。
である。
従って、
（14）により、
（15）
１男２男３男４
に於ける、
４の位置で、女子２人（Ａ、Ｂ）が隣り合う場合の、「場合の数」は、
（１２０－７２）÷４＝１２通り。
である。
然るに、
（16）
①ＡＢＣＤＥ
①ＡＢＣＥＤ
①ＡＢＤＣＥ
①ＡＢＤＥＣ
①ＡＢＥＣＤ
①ＡＢＥＤＣ
②ＡＣＢＤＥ
②ＡＣＢＥＤ
②ＡＣＤＢＥ
②ＡＣＤＥＢ
②ＡＣＥＢＤ
②ＡＣＥＤＢ
③ＡＤＢＣＥ
③ＡＤＢＥＣ
③ＡＤＣＢＥ
③ＡＤＣＥＢ
③ＡＤＥＢＣ
③ＡＤＥＣＢ
④ＡＥＢＣＤ
④ＡＥＢＤＣ
④ＡＥＣＢＤ
④ＡＥＣＤＢ
④ＡＥＤＢＣ
④ＡＥＤＣＢ
①ＢＡＣＤＥ
①ＢＡＣＥＤ
①ＢＡＤＣＥ
①ＢＡＤＥＣ
①ＢＡＥＣＤ
①ＢＡＥＤＣ
②ＢＣＡＤＥ
②ＢＣＡＥＤ
②ＢＣＤＡＥ
②ＢＣＤＥＡ
②ＢＣＥＡＤ
②ＢＣＥＤＡ
③ＢＤＡＣＥ
③ＢＤＡＥＣ
③ＢＤＣＡＥ
③ＢＤＣＥＡ
③ＢＤＥＡＣ
③ＢＤＥＣＡ
④ＢＥＡＣＤ
④ＢＥＡＤＣ
④ＢＥＣＡＤ
④ＢＥＣＤＡ
④ＢＥＤＡＣ
④ＢＥＤＣＡ
①ＣＡＢＤＥ
①ＣＡＢＥＤ
①ＣＡＤＢＥ
①ＣＡＤＥＢ
①ＣＡＥＢＤ
①ＣＡＥＤＢ
②ＣＢＡＤＥ
②ＣＢＡＥＤ
②ＣＢＤＡＥ
②ＣＢＤＥＡ
②ＣＢＥＡＤ
②ＣＢＥＤＡ
③ＣＤＡＢＥ
③ＣＤＡＥＢ
③ＣＤＢＡＥ
③ＣＤＢＥＡ
③ＣＤＥＡＢ
③ＣＤＥＢＡ
④ＣＥＡＢＤ
④ＣＥＡＤＢ
④ＣＥＢＡＤ
④ＣＥＢＤＡ
④ＣＥＤＡＢ
④ＣＥＤＢＡ
①ＤＡＢＣＥ
①ＤＡＢＥＣ
①ＤＡＣＢＥ
①ＤＡＣＥＢ
①ＤＡＥＢＣ
①ＤＡＥＣＢ
②ＤＢＡＣＥ
②ＤＢＡＥＣ
②ＤＢＣＡＥ
②ＤＢＣＥＡ
②ＤＢＥＡＣ
②ＤＢＥＣＡ
③ＤＣＡＢＥ
③ＤＣＡＥＢ
③ＤＣＢＡＥ
③ＤＣＢＥＡ
③ＤＣＥＡＢ
③ＤＣＥＢＡ
④ＤＥＡＢＣ
④ＤＥＡＣＢ
④ＤＥＢＡＣ
④ＤＥＢＣＡ
④ＤＥＣＡＢ
④ＤＥＣＢＡ
①ＥＡＢＣＤ
①ＥＡＢＤＣ
①ＥＡＣＢＤ
①ＥＡＣＤＢ
①ＥＡＤＢＣ
①ＥＡＤＣＢ
②ＥＢＡＣＤ
②ＥＢＡＤＣ
②ＥＢＣＡＤ
②ＥＢＣＤＡ
②ＥＢＤＡＣ
②ＥＢＤＣＡ
③ＥＣＡＢＤ
③ＥＣＡＤＢ
③ＥＣＢＡＤ
③ＥＣＢＤＡ
③ＥＣＤＡＢ
③ＥＣＤＢＡ
④ＥＤＡＢＣ
④ＥＤＡＣＢ
④ＥＤＢＡＣ
④ＥＤＢＣＡ
④ＥＤＣＡＢ
④ＥＤＣＢＡ
従って、
（15）（16）により、
（17）
果たして、
１男２男３男４
に於ける、
４の位置で、女子２人（Ａ、Ｂ）が隣り合う場合の、「場合の数」は、
（１２０－７２）÷４＝１２通り。
である。
（01）
①ＡＢＣ
②ＡＣＢ
③ＢＡＣ
④ＢＣＡ
⑤ＣＡＢ
⑥ＣＢＡ
従って、
（01）により、
（02）
「3Ｐ3＝３！＝３×２×１＝６通り」は、
｛Ａ、Ｂ、Ｃ｝から｛３つを取り出して、並べた｝際の「並べ方」である。
従って、
（03）
①ＡＢＣ
②ＡＣＢ
③ＢＡＣ
④ＢＣＡ
⑤ＣＡＢ
⑥ＣＢＡ
に対して、「ＥＤ」、または、「ＤＥ」を加へた、
①ＡＢＣＤＥ
②ＡＢＣＥＤ
③ＡＣＢＤＥ
④ＡＣＢＥＤ
⑤ＢＡＣＤＥ
⑥ＢＡＣＥＤ
⑦ＢＣＡＤＥ
⑧ＢＣＡＥＤ
⑨ＣＡＢＤＥ
⑩ＣＡＢＥＤ
⑪ＣＢＡＤＥ
⑫ＣＢＡＥＤ
は、「６×２＝１２通り」である。
従って、
（01）（02）（03）により、
（04）
｛Ａ、Ｂ、Ｃ｝＝｛男、男、男｝
｛Ｅ、Ｄ｝＝｛女、女｝
であるとして、
男子３人、女子２人が、一列に並ぶとき、
女子の２人が「４番と５番」に並ぶ、並び方は何通りか。
といふ「問題」の「答へ」は、「１２通り」である。
然るに、
（05）
①ＡＢＣＤＥ
②ＡＢＣＥＤ
に対して、
①ＡＢＣＤＥ
①ＡＢＤＥＣ
①ＡＤＥＢＣ
①ＤＥＡＢＣ
②ＡＢＣＥＤ
②ＡＢＥＤＣ
②ＡＥＤＢＣ
②ＥＤＡＢＣ
従って、
（03）（04）（05）により、
（06）
男子３人、女子２人が、一列に並ぶとき、
女子の２人が「隣り合う」並び方は何通りか。
といふ「問題」の「答へ」は、「１２×４＝４８通り」である。
然るに、
（07）
①ＡＢＣＤＥ ①ＡＢＣＥＤ ①ＡＢＤＣＥ ①ＡＢＤＥＣ ①ＡＢＥＣＤ ①ＡＢＥＤＣ ②ＡＣＢＤＥ ②ＡＣＢＥＤ ②ＡＣＤＢＥ ②ＡＣＤＥＢ ②ＡＣＥＢＤ ②ＡＣＥＤＢ ③ＡＤＢＣＥ ③ＡＤＢＥＣ ③ＡＤＣＢＥ ③ＡＤＣＥＢ ③ＡＤＥＢＣ ③ＡＤＥＣＢ ④ＡＥＢＣＤ ④ＡＥＢＤＣ ④ＡＥＣＢＤ ④ＡＥＣＤＢ ④ＡＥＤＢＣ ④ＡＥＤＣＢ ①ＢＡＣＤＥ ①ＢＡＣＥＤ ①ＢＡＤＣＥ ①ＢＡＤＥＣ ①ＢＡＥＣＤ ①ＢＡＥＤＣ ②ＢＣＡＤＥ ②ＢＣＡＥＤ ②ＢＣＤＡＥ ②ＢＣＤＥＡ ②ＢＣＥＡＤ ②ＢＣＥＤＡ ③ＢＤＡＣＥ ③ＢＤＡＥＣ ③ＢＤＣＡＥ ③ＢＤＣＥＡ ③ＢＤＥＡＣ ③ＢＤＥＣＡ ④ＢＥＡＣＤ ④ＢＥＡＤＣ ④ＢＥＣＡＤ ④ＢＥＣＤＡ ④ＢＥＤＡＣ ④ＢＥＤＣＡ ①ＣＡＢＤＥ ①ＣＡＢＥＤ ①ＣＡＤＢＥ ①ＣＡＤＥＢ ①ＣＡＥＢＤ ①ＣＡＥＤＢ ②ＣＢＡＤＥ ②ＣＢＡＥＤ ②ＣＢＤＡＥ ②ＣＢＤＥＡ ②ＣＢＥＡＤ ②ＣＢＥＤＡ ③ＣＤＡＢＥ ③ＣＤＡＥＢ ③ＣＤＢＡＥ ③ＣＤＢＥＡ ③ＣＤＥＡＢ ③ＣＤＥＢＡ ④ＣＥＡＢＤ ④ＣＥＡＤＢ ④ＣＥＢＡＤ ④ＣＥＢＤＡ ④ＣＥＤＡＢ ④ＣＥＤＢＡ ①ＤＡＢＣＥ ①ＤＡＢＥＣ ①ＤＡＣＢＥ ①ＤＡＣＥＢ ①ＤＡＥＢＣ ①ＤＡＥＣＢ ②ＤＢＡＣＥ ②ＤＢＡＥＣ ②ＤＢＣＡＥ ②ＤＢＣＥＡ ②ＤＢＥＡＣ ②ＤＢＥＣＡ ③ＤＣＡＢＥ ③ＤＣＡＥＢ ③ＤＣＢＡＥ ③ＤＣＢＥＡ ③ＤＣＥＡＢ ③ＤＣＥＢＡ ④ＤＥＡＢＣ ④ＤＥＡＣＢ ④ＤＥＢＡＣ ④ＤＥＢＣＡ ④ＤＥＣＡＢ ④ＤＥＣＢＡ ①ＥＡＢＣＤ ①ＥＡＢＤＣ ①ＥＡＣＢＤ ①ＥＡＣＤＢ ①ＥＡＤＢＣ ①ＥＡＤＣＢ ②ＥＢＡＣＤ ②ＥＢＡＤＣ ②ＥＢＣＡＤ ②ＥＢＣＤＡ ②ＥＢＤＡＣ ②ＥＢＤＣＡ ③ＥＣＡＢＤ ③ＥＣＡＤＢ ③ＥＣＢＡＤ ③ＥＣＢＤＡ ③ＥＣＤＡＢ ③ＥＣＤＢＡ ④ＥＤＡＢＣ ④ＥＤＡＣＢ ④ＥＤＢＡＣ ④ＥＤＢＣＡ ④ＥＤＣＡＢ ④ＥＤＣＢＡ
従って、
（05）（06）（07）により、
（08）
｛Ａ、Ｂ、Ｃ｝＝｛男、男、男｝
｛Ｅ、Ｄ｝＝｛女、女｝
であるとして、
男子３人、女子２人が、一列に並ぶとき、
女子の２人が「４番と５番」に並ぶ、並び方は何通りか。
といふ「問題」の「答へ」は、「１２通り」である。
と「同時」に、
女子の２人が「１番と２番」に並ぶ、並び方は何通りか。
女子の２人が「２番と３番」に並ぶ、並び方は何通りか。
女子の２人が「３番と４番」に並ぶ、並び方は何通りか。
女子の２人が「５番と６番」に並ぶ、並び方は何通りか。
といふ「問題」に対する「答へ」は、４つとも、
（５－２）！×２！＝（３×２×１）×（２×１）＝１２通り。
である。
然るに、
（09）
５！＝５×４×３×２×１＝１２０通り。
であるため、
男子３人、女子２人が、一列に並ぶ「並び方」は、１２０通り。
である。
従って、
（08）（09）により、
（10）
男子３人、女子２人が、一列に、「ランダム」に並ぶとき、
女子の２人が「１番と２番」に並ぶ「確率」。
女子の２人が「２番と３番」に並ぶ「確率」。
女子の２人が「３番と４番」に並ぶ「確率」。
女子の２人が「５番と６番」に並ぶ「確率」。
は、４つとも、
｛（５－２）！×２！｝÷５！＝１２÷１２０＝０.１＝１０％
である。
従って、
（10）により、
（11）
男子３人、女子２人が、一列に、「ランダム」に並ぶとき、
女子の２人が「５番と６番」に並ぶ「確率」。
に「意味」があるとするならば、
女子の２人が「１番と２番」に並ぶ「確率」。
女子の２人が「２番と３番」に並ぶ「確率」。
女子の２人が「３番と４番」に並ぶ「確率」。
にも「意味」がなければ、ならない。
然るに、
（12）
男子３人は、高校３年生で、
女子２人は、小学１年生である。
とする。
然るに、
（13）
出典：学校保健統計調査
従って、
（11）（12）（13）により、
（14）
男子３人（高校３年生）、
女子２人（小学１年生）が、一列に、「身長順」に並ぶとき、
女子の２人が「１番と２番」に並ぶ「確率」。
女子の２人が「２番と３番」に並ぶ「確率」。
女子の２人が「３番と４番」に並ぶ「確率」。
女子の２人が「５番と６番」に並ぶ「確率」。
は、「同じ（１０％）」になるはずが無い。
従って、
（11）～（14）により、
（15）
男子３人、女子２人が、一列に、「ランダム」に並ぶ際に、
女子の２人が「５番と６番」に並ぶ「確率（は１０％である）。
といふことには、「意味」が無いものの、
男子３人（高校３年生）、
女子２人（小学１年生）が、一列に、「身長順」に並ぶとき、
女子の２人が「５番と６番」に並ぶ「確率（が極めて高い）。」
といふことには、「意味」が有る。
然るに、
（16）
従って、
（16）により、
（17）
『点滴をすると、血液が薄くなり、血液が薄くなると、「赤血球の数値」が低くなる。』
といふ「仮説」を考へてゐる場合には、
「３６回の血液検査（点滴無し）」の「赤血球の数値」と、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」を、
「ランダム」に並べた場合に、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」が、
「３７番目、３８番目、３９番目、４０番目、４１番目」のいづれかになる場合の「確率」には、「意味」がある。
然るに、
（10）により、
（18）
「３６回の血液検査（点滴無し）」の「赤血球の数値」と、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」を、
「ランダム」に並べた場合に、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」が、
「３７番目、３８番目、３９番目、４０番目、４１番目」のいづれかになる場合の「確率」は、
｛（４１－５）！×５！｝÷４１！＝（１÷７４９３９４）≒0.0000013344（約７５万分の１）。
である。
従って、
（18）により、
（19）
「３６回の血液検査（点滴無し）」の「赤血球の数値」と、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」を、
「ランダム」に並べた場合に、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」が、
「３７番目、３８番目、３９番目、４０番目、４１番目」のいづれかになる場合の「確率」は、
「０．０００１４％以下」である。
然るに、
（20）
（18）（19）（20）により、
（21）
「３６回の血液検査（点滴無し）」の「赤血球の数値」と、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」を、
「ランダム」に並べた場合に、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」が、
「３７番目、３８番目、３９番目、４０番目、４１番目」のいづれかになる場合の「確率」は、「０．０００１４％以下」であるが、
「３６回の血液検査（点滴無し）」の「赤血球の数値」と、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」を、「数値の大きい順」に並べたところ、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」は、 「３７番目、３８番目、３９番目、４０番目、４１番目」のいづれかになってゐる。
従って、
（17）（21）により、
（22）
『点滴をすると、血液が薄くなり、血液が薄くなると、「赤血球の数値」が低くなる。』
といふ「推定」は「正しい」。
（23）
そもそも統計学という学問は、数学の分野なのだ。
数式を使って理解することが大前提である。
統計学にとって数字や数式は「言語」であり、それなくして理解できないようになっている。
（高橋洋一、図解 統計学（超）入門、2018年、４頁）
従って、
（24）
出来れば、
のやうな「教科書（医学書院、臨床検査技師講座１）」で、『推計学』といふ「数学」を学んだ上で、「医療裁判」に臨みたいものの、『高校数学Ａ』を理解するのがやっとである私には、そのやうなことをしてゐる、「時間的な余裕」がない。
（16）により、
（17）
『点滴をすると、血液が薄くなり、血液が薄くなると、「赤血球の数値」が低くなる。』
といふ「仮説」を考へてゐる場合には、
「３６回の血液検査（点滴無し）」の「赤血球の数値」と、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」を、
「ランダム」に並べた場合に、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」が、
「３７番目、３８番目、３９番目、４０番目、４１番目」のいづれかになる場合の「確率」には、「意味」がある。
然るに、
（10）により、
（18）
「３６回の血液検査（点滴無し）」の「赤血球の数値」と、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」を、
「ランダム」に並べた場合に、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」が、
「３７番目、３８番目、３９番目、４０番目、４１番目」のいづれかになる場合の「確率」は、
｛（４１－５）！×５！｝÷４１！＝（１÷７４９３９４）≒0.0000013344（約７５万分の１）。
である。
従って、
（18）により、
（19）
「３６回の血液検査（点滴無し）」の「赤血球の数値」と、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」を、
「ランダム」に並べた場合に、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」が、
「３７番目、３８番目、３９番目、４０番目、４１番目」のいづれかになる場合の「確率」は、
「０．０００１４％以下」である。
然るに、
（20）
（21）
「３６回の血液検査（点滴無し）」の「赤血球の数値」と、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」を、
「ランダム」に並べた場合に、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」が、
「３７番目、３８番目、３９番目、４０番目、４１番目」のいづれかになる場合の「確率」は、「０．０００１４％以下」であるが、
「３６回の血液検査（点滴無し）」の「赤血球の数値」と、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」を、「数値の大きい順」に並べたところ、
「 ５回の血液検査（点滴有り）」の「赤血球の数値」は、 「３７番目、３８番目、３９番目、４０番目、４１番目」のいづれかになってゐる。
従って、
（17）（21）により、
（22）
『点滴をすると、血液が薄くなり、血液が薄くなると、「赤血球の数値」が低くなる。』
といふ「推定」は「正しい」。
（23）
そもそも統計学という学問は、数学の分野なのだ。
数式を使って理解することが大前提である。
統計学にとって数字や数式は「言語」であり、それなくして理解できないようになっている。
（高橋洋一、図解 統計学（超）入門、2018年、４頁）
従って、
（24）
出来れば、
（01）
①ＡＢＣ
②ＡＣＢ
③ＢＡＣ
④ＢＣＡ
⑤ＣＡＢ
⑥ＣＢＡ
従って、
（01）により、
（02）
｛Ａ、Ｂ、Ｃ｝から｛３つを取り出して、並べた｝際の「並べ方」は、
3Ｐ3＝３！＝３×２×１＝６通り。
従って、
（02）により、
（03）
①ＡＢＣ
②ＡＣＢ
③ＢＡＣ
④ＢＣＡ
⑤ＣＡＢ
⑥ＣＢＡ
に対して、「ＥＤ」を加へた、
①ＡＢＣＥＤ
②ＡＣＢＥＤ
③ＢＡＣＥＤ
④ＢＣＡＥＤ
⑤ＣＡＢＥＤ
⑥ＣＢＡＥＤ
も、「６通り」である。
従って、
（03）により、
（04）
①ＡＢＣ
②ＡＣＢ
③ＢＡＣ
④ＢＣＡ
⑤ＣＡＢ
⑥ＣＢＡ
に対して、「ＤＥ」を加へた、
①ＡＢＣＤＥ
②ＡＣＢＤＥ
③ＢＡＣＤＥ
④ＢＣＡＤＥ
⑤ＣＡＢＤＥ
⑥ＣＢＡＤＥ
も、「６通り」である。
従って、
（03）（04）により、
（05）
①ＡＢＣ
②ＡＣＢ
③ＢＡＣ
④ＢＣＡ
⑤ＣＡＢ
⑥ＣＢＡ
に対して、「ＥＤ」、
または、 「ＤＥ」を加へた、
①ＡＢＣＤＥ
②ＡＢＣＥＤ
③ＡＣＢＤＥ
④ＡＣＢＥＤ
⑤ＢＡＣＤＥ
⑥ＢＡＣＥＤ
⑦ＢＣＡＤＥ
⑧ＢＣＡＥＤ
⑨ＣＡＢＤＥ
⑩ＣＡＢＥＤ
⑪ＣＢＡＤＥ
⑫ＣＢＡＥＤ
は、「６×２＝１２通り」である。
然るに、
（06）
｛Ａ、Ｂ、Ｃ、Ｄ、Ｅ｝から｛５つを取り出して、並べた｝際の「並べ方」は、
「5Ｐ5＝５！＝５×４×３×２×１＝１２０通り」である。
従って、
（05）（06）により、
（07）
｛Ａ、Ｂ、Ｃ、Ｄ、Ｅ｝から｛５つを取り出して、並べた｝際の、
5Ｐ5＝５！＝５×４×３×２×１＝１２０通り。
の中には、
①ＡＢＣＤＥ
②ＡＢＣＥＤ
③ＡＣＢＤＥ
④ＡＣＢＥＤ
⑤ＢＡＣＤＥ
⑥ＢＡＣＥＤ
⑦ＢＣＡＤＥ
⑧ＢＣＡＥＤ
⑨ＣＡＢＤＥ
⑩ＣＡＢＥＤ
⑪ＣＢＡＤＥ
⑫ＣＢＡＥＤ
といふ「６×２＝１２通り」が、含まれてゐる。
然るに、
（08）
ＡＢＣＤＥ①
ＡＢＣＥＤ②
ＡＢＤＣＥ
ＡＢＤＥＣ
ＡＢＥＣＤ
ＡＢＥＤＣ
ＡＣＢＤＥ③
ＡＣＢＥＤ④
ＡＣＤＢＥ
ＡＣＤＥＢ
ＡＣＥＢＤ
ＡＣＥＤＢ
ＡＤＢＣＥ
ＡＤＢＥＣ
ＡＤＣＢＥ
ＡＤＣＥＢ
ＡＤＥＢＣ
ＡＤＥＣＢ
ＡＥＢＣＤ
ＡＥＢＤＣ
ＡＥＣＢＤ
ＡＥＣＤＢ
ＡＥＤＢＣ
ＡＥＤＣＢ
ＢＡＣＤＥ⑤
ＢＡＣＥＤ⑥
ＢＡＤＣＥ
ＢＡＤＥＣ
ＢＡＥＣＤ
ＢＡＥＤＣ
ＢＣＡＤＥ⑦
ＢＣＡＥＤ⑧
ＢＣＤＡＥ
ＢＣＤＥＡ
ＢＣＥＡＤ
ＢＣＥＤＡ
ＢＤＡＣＥ
ＢＤＡＥＣ
ＢＤＣＡＥ
ＢＤＣＥＡ
ＢＤＥＡＣ
ＢＤＥＣＡ
ＢＥＡＣＤ
ＢＥＡＤＣ
ＢＥＣＡＤ
ＢＥＣＤＡ
ＢＥＤＡＣ
ＢＥＤＣＡ
ＣＡＢＤＥ⑨
ＣＡＢＥＤ⑩
ＣＡＤＢＥ
ＣＡＤＥＢ
ＣＡＥＢＤ
ＣＡＥＤＢ
ＣＢＡＤＥ⑪
ＣＢＡＥＤ⑫
ＣＢＤＡＥ
ＣＢＤＥＡ
ＣＢＥＡＤ
ＣＢＥＤＡ
ＣＤＡＢＥ
ＣＤＡＥＢ
ＣＤＢＡＥ
ＣＤＢＥＡ
ＣＤＥＡＢ
ＣＤＥＢＡ
ＣＥＡＢＤ
ＣＥＡＤＢ
ＣＥＢＡＤ
ＣＥＢＤＡ
ＣＥＤＡＢ
ＣＥＤＢＡ
ＤＡＢＣＥ
ＤＡＢＥＣ
ＤＡＣＢＥ
ＤＡＣＥＢ
ＤＡＥＢＣ
ＤＡＥＣＢ
ＤＢＡＣＥ
ＤＢＡＥＣ
ＤＢＣＡＥ
ＤＢＣＥＡ
ＤＢＥＡＣ
ＤＢＥＣＡ
ＤＣＡＢＥ
ＤＣＡＥＢ
ＤＣＢＡＥ
ＤＣＢＥＡ
ＤＣＥＡＢ
ＤＣＥＢＡ
ＤＥＡＢＣ
ＤＥＡＣＢ
ＤＥＢＡＣ
ＤＥＢＣＡ
ＤＥＣＡＢ
ＤＥＣＢＡ
ＥＡＢＣＤ
ＥＡＢＤＣ
ＥＡＣＢＤ
ＥＡＣＤＢ
ＥＡＤＢＣ
ＥＡＤＣＢ
ＥＢＡＣＤ
ＥＢＡＤＣ
ＥＢＣＡＤ
ＥＢＣＤＡ
ＥＢＤＡＣ
ＥＢＤＣＡ
ＥＣＡＢＤ
ＥＣＡＤＢ
ＥＣＢＡＤ
ＥＣＢＤＡ
ＥＣＤＡＢ
ＥＣＤＢＡ
ＥＤＡＢＣ
ＥＤＡＣＢ
ＥＤＢＡＣ
ＥＤＢＣＡ
ＥＤＣＡＢ
ＥＤＣＢＡ
従って、
（07）（08）により、
（09）
｛Ａ、Ｂ、Ｃ、Ｄ、Ｅ｝から｛５つを取り出して、並べた｝際の、
5Ｐ5＝５！＝５×４×３×２×１＝１２０通り。
の中には、実際に、
①ＡＢＣＤＥ
②ＡＢＣＥＤ
③ＡＣＢＤＥ
④ＡＣＢＥＤ
⑤ＢＡＣＤＥ
⑥ＢＡＣＥＤ
⑦ＢＣＡＤＥ
⑧ＢＣＡＥＤ
⑨ＣＡＢＤＥ
⑩ＣＡＢＥＤ
⑪ＣＢＡＤＥ
⑫ＣＢＡＥＤ
といふ「６×２＝１２通り」が、含まれてゐる。
従って、
（07）（08）（09）により、
（10）
｛Ａ、Ｂ、Ｃ、Ｄ、Ｅ｝から｛５つを取り出して、並べた｝際の、
5Ｐ5＝５！＝５×４×３×２×１＝１２０通り。
の中には、
①ＤＥＣＡＢ
②ＤＥＣＢＡ
③ＤＣＥＡＢ
④ＤＣＥＢＡ
⑤ＥＤＣＡＢ
⑥ＥＤＣＢＡ
⑦ＥＣＤＡＢ
⑧ＥＣＤＢＡ
⑨ＣＤＥＡＢ
⑩ＣＤＥＢＡ
⑪ＣＥＤＡＢ
⑫ＣＥＤＢＡ
といふ「６×２＝１２通り」が、含まれてゐる。
従って、
（09）（10）により、
（11）
｛Ａ、Ｂ、Ｃ、Ｄ、Ｅ｝から、『ランダム』に、｛５つを取り出して、並べた｝際に、
｛＃、＃、＃、Ｄ、Ｅ｝または、
｛＃、＃、＃、Ｅ、Ｄ｝といふ「順番」で並ぶ「確率」は、
｛（５－２）！×２！｝÷５！＝１２÷１２０＝０．１
である。
従って、
（11）により、
（12）
｛Ａ、Ｂ、Ｃ、Ｄ、Ｅ｝や、
｛ア、イ、ウ、エ、オ｝を含む｛４１個の要素｝から、『ランダム』に、｛４１個を取り出して、並べた｝際に、
｛＃、＃、・・・・・・・、ア、イ、ウ、エ、オ｝や、
｛＃、＃、・・・・・・・、オ、エ、ウ、イ、ア｝といふ「順番」で並ぶ「確率」は、
｛（４１－５）！×５！｝÷４１！＝（１÷７４９３９４）≒0.0000013344（約７５万分の１）。
である。
従って、
（12）により、
（13）
｛ア、イ、ウ、エ、オ｝を含む｛４１個の要素｝から、『ランダム』に、｛４１個を取り出して、並べた｝際に、
｛Ａ、Ｂ、・・・・・・・、ア、イ、ウ、エ、オ｝や、
｛Ｆ、Ｑ、・・・・・・・、ウ、エ、オ、ア、イ｝や、
｛Ｒ、Ｚ、・・・・・・・、オ、エ、ウ、イ、ア｝といふ「順番」で並ぶ「確率」は、 「０.０００１４％」にも、満たない。
従って、
（14）
｛２０１８年１月２６日、２０１９年１月０４日、２０１９年１月１１日、２０１９年１月１８日、２０１９年１月２９日｝
を含む｛４１個の日付｝から、『ランダム』に、｛４１個を取り出して、並べた｝際に、
｛＃、＃、・・・・、２０１８年１月２６日、２０１９年１月０４日、２０１９年１月１１日、２０１９年１月１８日、２０１９年１月２９日｝や、
｛＃、＃、・・・・、２０１９年１月２９日、２０１９年１月１８日、２０１８年１月２６日、２０１９年１月１１日、２０１９年１月０４日｝といふ「順番」で並ぶ「確率」は、
「０.０００１４％」にも、満たない。
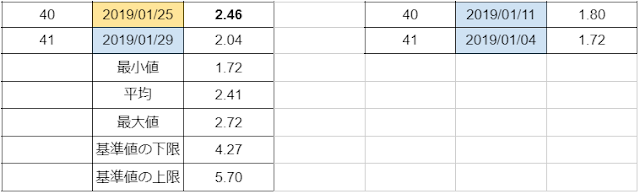
然るに、
（15）
従って、
（14）（15）により、
（16）
「０.０００１４％」にも満たない、「確率」からすれば、
｛２０１２年６月１８日｝から｛２０１９年１月２９日｝までの、｛４１回の血液検査｝に於いて、
｛２０１８年１月２６日、２０１９年１月０４日、２０１９年１月１１日、２０１９年１月１８日、２０１９年１月２９日｝といふ｛５回｝だけが、
｛点滴の最中｝であって、尚且つ、
｛２０１８年１月２６日、２０１９年１月０４日、２０１９年１月１１日、２０１９年１月１８日、２０１９年１月２９日｝といふ｛５回｝の｛数値｝が、
｛大きい順｝に並べた際に、
｛３７番目、３８番目、３９番目、４０番目、４１番目｝
である。
といふことは、「単なる偶然」ではあり得ない。
然るに、
（17）
従って、
（16）（17）により、
（18）
『点滴をすると、血液が薄くなり、血液が薄く成ると、血液検査の際の、「赤血球の値」が低くなる。』
といふ「推定」は、「正しい」。
然るに、
（19）
（16）（17）により、
（18）
『点滴をすると、血液が薄くなり、血液が薄く成ると、血液検査の際の、「赤血球の値」が低くなる。』
といふ「推定」は、「正しい」。
然るに、
（19）
従って、
（19）により、
（20）
従って、
（19）により、
（20）
①「脱水」であるならば、（「点滴」をすれば、「数値は下降する」）。
という風に、鈴木医師は、述べてゐる。
然るに、
（21）
（ⅰ）
１ （１） Ｐ→（Ｑ→ Ｒ） Ａ
２ （２） Ｑ＆～Ｒ Ａ
３（３） Ｑ→ Ｒ Ａ
２ （４） Ｑ ２＆Ｅ
２３（５） Ｒ ３４ＭＰＰ
３（６） ～Ｒ ２＆Ｅ
２３（７） Ｒ＆～Ｒ ５６＆Ｉ
２ （８） ～（Ｑ→ Ｒ） ３７ＲＡＡ
１２ （９）～Ｐ １８ＭＴＴ
１ （ア）（Ｑ＆～Ｒ）→～Ｐ ２９ＣＰ
（ⅱ）
１ （１） （Ｑ＆～Ｒ）→～Ｐ Ａ
２ （２） Ｐ Ａ
２ （３） ～～Ｐ ２ＤＮ
１２ （４）～（Ｑ＆～Ｒ） １３ＭＴＴ
５ （５） Ｑ Ａ
６（６） ～Ｒ Ａ
５６（７） Ｑ＆～Ｒ ５６＆Ｉ
１２５６（８）～（Ｑ＆～Ｒ）＆
（Ｑ＆～Ｒ） ４７＆Ｉ
１２５ （９） ～～Ｒ ６８ＲＡＡ
１２５ （ア） Ｒ ９ＤＮ
１２ （イ） Ｑ→Ｒ ５アＣＰ
１ （ウ）Ｐ→（Ｑ→Ｒ） ２イＣＰ
従って、
（21）により、
（22）
① Ｐ→（Ｑ→Ｒ）
②（Ｑ＆～Ｒ）→～Ｐ
に於いて、
①＝② は「対偶」である。
従って、
（22）により、
（23）
Ｐ＝「脱水」である。
Ｑ＝「点滴」をする。
Ｒ＝「数値は下降する」。
とするならば、
① 「脱水」であるならば、（「点滴」をすれば、「数値は下降する」）。
②（「点滴」をしても、「数値が下降しない」）のであれば、「脱水」ではない。
に於いて、 ①＝② は、「対偶」である。
然るに、
（24）
従って、
（23）（24）により、
（25）
クレアチニンの、
２０１９年１月１８日から、
２０１９年１月２５日にかけての、
といふことは、有り得ない。
従って、
（25）により、
（26）
といふ『診断』、すなはち、
２０１９年１月１８日から、
２０１９年１月２５日にかけての、『急性腎不全』の「原因」は「脱水」である。
２０１９年１月２５日にかけての、『急性腎不全』の「原因」は「脱水」である。
といふ『診断』は、『誤診』である。
（26）
出来れば、
といふ「教科書」で、『推計学』といふ「数学」を学んだ上で、「医療裁判」に臨みたいものの、『高校数学Ａ』を理解するのがやっとである私には、そのやうなことをしてゐる、「時間的な余裕」はない。
（01）
（ⅰ）
１ （１）∀ｘ（象ｘ→動物ｘ） Ａ
１ （２） 象ａ→動物ａ １ＵＥ
３（３） 象ａ Ａ
１３（４） 動物ａ ２３ＭＰＰ
１３（５） 象ａ＆動物ａ ３４＆Ｉ
１ （６） 象ａ→象ａ＆動物ａ ３５ＣＰ
１ （７）∀ｘ（象ｘ→象ｘ＆動物ｘ） ６ＵＩ
（ⅱ）
１ （１）∀ｘ（象ｘ→象ｘ＆動物ｘ） Ａ
１ （２） 象ａ→象ａ＆動物ａ １ＵＥ
３（３） 象ａ Ａ
１３（４） 象ａ＆動物ａ ２３ＭＰＰ
１３（５） 動物ａ ４＆Ｅ
１ （６） 象ａ→動物ａ ３５ＣＰ
１ （７）∀ｘ（象ｘ→動物ｘ） １ＵＩ
従って、
（01）により、
（02）
① ∀ｘ（象ｘ→動物ｘ）
② ∀ｘ（象ｘ→象ｘ＆動物ｘ）
に於いて、
①＝② である。
従って、
（02）により、
（03）
① すべてのｘについて（ｘが象であるならば、ｘは動物である）。
② すべてのｘについて（ｘが象であるならば、ｘは象であって、ｘは動物である）。
に於いて、
①＝② である。
従って、
（03）により、
（04）
① 象は、動物である。
② 象は、象といふ動物である。
に於いて、
①＝② である。
然るに、
（05）
③ 象
④ 象といふ動物
に於いて、
③＝④ であるに、違ひない。
然るに、
（02）により、
（06）
① ∀ｘ（象ｘ→～動物ｘ）
② ∀ｘ（象ｘ→象ｘ＆～動物ｘ）
に於いて、
①＝② である。
従って、
（04）（05）（06）により、
（07）
「象のクラス」が、「動物のクラスのメンバー」であるならば、そのときに限って、
「象のクラス」は、「象といふ動物のクラス」に、「等しい」。
然るに、
（08）
「象のクラス」以外にも、例へば、「ライオンのクラス」も、「動物のクラスのメンバー」である。
従って、
（08）により、
（09）
「動物のクラス」は、「象のクラス」よりも、「大きい」。
従って、
（07）（08）（09）により、
（10）
「象といふ動物のクラス」は、「動物のクラス」よりも、「小さい」。
従って、
（07）（10）により、
（11）
「内包」が「増へる」と、場合によっては、「クラス」は、「縮小」する。
（01）
①（集合Ａが集合Ｂの部分集合である）ならば、そのときに限って（集合Ａと集合Ｂの和集合は、集合Ｂに等しい）。
②（集合Ａが集合Ｂの部分集合である）ならば、そのときに限って（集合Ａと集合Ｂの積集合は、集合Ａに等しい）。
といふ「命題」は、
①（Ａ⊆Ｂ）⇔（Ａ∪Ｂ＝Ｂ）
②（Ａ⊆Ｂ）⇔（Ａ∩Ｂ＝Ａ）
といふ「集合の式」で、表すことが出来る。
然るに、
（02）
Ａ＝ｘは集合Ａの要素である（ｘ∈Ａ）。
Ｂ＝ｘは集合Ｂの要素である（ｘ∈Ｂ）。
Ａ∨Ｂ＝ｘは集合Ａの要素であるか、または、ｘは集合Ｂの要素である（ｘ∈Ａ∨ｘ∈Ｂ）。
Ａ＆Ｂ＝ｘは集合Ａの要素であって、その上、ｘは集合Ｂの要素である（ｘ∈Ａ∨ｘ∈Ｂ）。
Ａ→Ｂ＝ｘが集合Ａの要素であるならば、 ｘは集合Ｂの要素である（ｘ∈Ａ→ｘ∈Ｂ）。
とするならば、
①（Ａ⊆Ｂ）⇔（Ａ∪Ｂ＝Ｂ）
②（Ａ⊆Ｂ）⇔（Ａ∩Ｂ＝Ａ）
といふ「集合の式」は、
①（Ａ→Ｂ）⇔（Ａ∨Ｂ⇔Ｂ）
②（Ａ→Ｂ）⇔（Ａ＆Ｂ⇔Ａ）
といふ「命題論理の式」に、「相当」する。
然るに、
（03）
（ⅰ）
１ （１） Ａ→Ｂ 仮定
２ （２） Ａ∨Ｂ 仮定
３ （３） Ａ 仮定
１ ３ （４） Ｂ １３ＭＰＰ
５ （５） Ｂ 仮定
１２ （６） Ｂ ２３４５５∨Ｅ
１ （７） Ａ∨Ｂ→Ｂ ２６ＣＰ
８ （８） Ｂ 仮定
８ （９） Ａ∨Ｂ ８∨Ｉ
（ア） Ｂ→Ａ∨Ｂ ８９ＣＰ
１ （イ）（Ａ∨Ｂ→Ｂ）＆
（Ｂ→Ａ∨Ｂ） ７ア＆Ｉ
１ （ウ） Ａ∨Ｂ⇔Ｂ イＤｆ.⇔
（エ）（Ａ→Ｂ）→（Ａ∨Ｂ⇔Ｂ） １ウＣＰ
オ （オ） Ａ∨Ｂ⇔Ｂ 仮定
オ （カ）（Ａ∨Ｂ→Ｂ）＆
（Ｂ→Ａ∨Ｂ） オＤｆ.⇔
オ （キ） Ａ∨Ｂ→Ｂ カ＆Ｅ
ク（ク） Ａ 仮定
ク（ケ） Ａ∨Ｂ ク∨Ｉ
オク（コ） Ｂ キケＭＰＰ
オ （サ） Ａ→Ｂ クコＣＰ
（シ）（Ａ∨Ｂ⇔Ｂ）→（Ａ→Ｂ） オサＣＰ
（ス）（Ａ→Ｂ）→（Ａ∨Ｂ⇔Ｂ）＆
（Ａ∨Ｂ⇔Ｂ）→（Ａ→Ｂ） エシ＆Ｉ
（セ）（Ａ→Ｂ）⇔（Ａ∨Ｂ⇔Ｂ） スＤｆ.⇔
（ⅱ）
１ （１） Ａ→Ｂ 仮定
２ （２） Ａ＆Ｂ 仮定
２ （３） Ｂ ２＆Ｅ
（４） Ａ＆Ｂ→Ｂ ２３ＣＰ
５ （５） Ａ 仮定
１ ５ （６） Ｂ １５ＭＰＰ
１ ５ （７） Ａ＆Ｂ ５６＆Ｉ
１ （８） Ａ→Ａ＆Ｂ ５７ＣＰ
１ （９）（Ａ＆Ｂ→Ａ）＆
（Ａ→Ａ＆Ｂ） ４９＆Ｉ
１ （ア） Ａ＆Ｂ⇔Ａ ９Ｄｆ.⇔
（イ）（Ａ→Ｂ）→（Ａ＆Ｂ⇔Ａ） １アＣＰ
ウ （ウ）（Ａ＆Ｂ⇔Ａ） Ａ
ウ （エ）（Ａ＆Ｂ→Ａ）＆
（Ａ→Ａ＆Ｂ） ウＤｆ.⇔
ウ （オ） Ａ→Ａ＆Ｂ エ＆Ｅ
カ（カ） Ａ Ａ
ウカ（キ） Ａ＆Ｂ オカＭＰＰ
ウカ（ク） Ｂ キ＆Ｅ
ウ （ケ） Ａ→Ｂ カクＣＰ
（コ）（Ａ＆Ｂ⇔Ａ）→（Ａ→Ｂ） ウケＣＰ
（サ）（Ａ→Ｂ）→（Ａ＆Ｂ⇔Ａ）＆
（Ａ＆Ｂ⇔Ａ）→（Ａ→Ｂ） イコ＆Ｉ
（シ）（Ａ→Ｂ）⇔（Ａ＆Ｂ⇔Ａ） サＤｆ.⇔
従って、
（03）により、
（04）
①（Ａ→Ｂ）⇔（Ａ∨Ｂ⇔Ｂ）
②（Ａ→Ｂ）⇔（Ａ＆Ｂ⇔Ａ）
といふ「命題論理式」に於いて、
① は「恒真式（トートロジー）」であって、
② も「恒真式（トートロジー）」である。
従って、
（01）～（04）により、
（05）
①（Ａ→Ｂ）⇔（Ａ∨Ｂ⇔Ｂ）
②（Ａ→Ｂ）⇔（Ａ＆Ｂ⇔Ａ）
といふ「命題論理式」に於いて、
① は「恒真式（トートロジー）」であって、
② も「恒真式（トートロジー）」であるが故に、
①（Ａ⊆Ｂ）⇔（Ａ∪Ｂ＝Ｂ）
②（Ａ⊆Ｂ）⇔（Ａ∩Ｂ＝Ａ）
といふ「集合の式」に於いても、
① は「恒真式（トートロジー）」であって、
② も「恒真式（トートロジー）」であるに、違ひない。
然るに、
（06）
練習２ Ａ⊆Ｂ⇔Ａ∪Ｂ＝Ｂ，また、Ａ⊆Ｂ⇔Ａ∩Ｂ＝Ａ を証明せよ。
（数研出版、チャート式 基礎からの確率・統計、初版 昭和４２年、１３頁）
然るに、
（05）（06）により、
（07）
「証明せよ」といふ「練習問題」がある以上、
①（Ａ⊆Ｂ）⇔（Ａ∪Ｂ＝Ｂ）
②（Ａ⊆Ｂ）⇔（Ａ∩Ｂ＝Ａ）
といふ「集合の式」は、二つとも、「恒真式（トートロジー）」である。
然るに、
（08）
「集合はクラスの特別の種類のものであると解釈される（E.J.レモン著、石橋新・高橋敬吾 訳、公理的集合論入門、1972年、序論）。」
「実際、その第一の段階において、クラスの理論は命題計算よりも難しいものではなく、また、以下に見られる通り、それは密接な類似性をもっている（E.J.レモン著、竹尾治一郎・浅野楢英 訳、論理学初歩、1973年、２５９頁）。」
従って、
（05）～（08）により、
（09）
①（Ａ→Ｂ）⇔（Ａ∨Ｂ⇔Ｂ）
②（Ａ→Ｂ）⇔（Ａ＆Ｂ⇔Ａ）
といふ「命題論理式」と、
①（Ａ⊆Ｂ）⇔（Ａ∪Ｂ＝Ｂ）
②（Ａ⊆Ｂ）⇔（Ａ∩Ｂ＝Ａ）
といふ「集合（クラス）の式」には、「密接な類似性（close resemblance）」がある。
然るに、
（10）
因みに、
（ａ）「E.J.レモン著、石橋新・高橋敬吾 訳、公理的集合論入門、1972年」
（ｂ）「E.J.レモン著、竹尾治一郎・浅野楢英 訳、論理学初歩、 1973年」
を「比較」すると、私にとっては、
（ａ）の方が、「格段に難しい」。
（11）
「高校数学」で「集合」と言へば、『ベン図』であるが、
「E.J.レモン著、公理的集合論入門、1972年」には、『ベン図』は、全く登場しない。
（12）
例題１ 分配法則 （Ａ∪Ｂ）∩Ｃ＝（Ａ∩Ｃ）∪（Ｂ∩Ｃ） を証明せよ。
（数研出版、チャート式 基礎からの確率・統計、初版 昭和４２年、１２頁）
の「解答」は、
といふやうな『ベン図』で示される。
然るに、
（13）
（Ａ∪Ｂ）∩Ｃ＝（Ａ∩Ｃ）∪（Ｂ∩Ｃ）
といふ「集合の式」を、
（Ａ∨Ｂ）＆Ｃ⇔（Ａ＆Ｃ）∨（Ｂ＆Ｃ）
と書くと、「見た瞬間に、そんなの当然」である。
ｃｆ.
（ⅰ）
１ （１）（Ａ∨Ｂ）＆Ｃ 仮定
１ （２） Ａ∨Ｂ １＆Ｅ
１ （３） Ｃ １＆Ｅ
４ （４） Ａ 仮定
１４ （５） Ａ＆Ｃ ３４＆Ｉ
１４ （６）（Ａ＆Ｃ）∨（Ｂ＆Ｃ） ５∨Ｉ
７（７） Ｂ 仮定
１ ７（８） Ｂ＆Ｃ ３７＆Ｉ
１ ７（９）（Ａ＆Ｃ）∨（Ｂ＆Ｃ） ８∨Ｉ
１ （ア）（Ａ＆Ｃ）∨（Ｂ＆Ｃ） ２４６７９∨Ｅ
（ⅱ）
１ （１）（Ａ＆Ｃ）∨（Ｂ＆Ｃ） 仮定
２ （２）（Ａ＆Ｃ） 仮定
２ （３） Ａ ２＆Ｅ
２ （４） Ａ∨Ｂ ３∨Ｉ
２ （５） Ｃ ２＆Ｅ
２ （６）（Ａ∨Ｂ）＆Ｃ ４５＆Ｅ
７（７） Ｂ＆Ｃ 仮定
７（８） Ｂ ７＆Ｅ
７（９） Ａ∨Ｂ ８∨Ｉ
７（ア） Ｃ ７＆Ｅ
７（イ） （Ａ∨Ｂ）＆Ｃ ９ア＆Ｉ
１ （ウ）（Ａ∨Ｂ）＆Ｃ １２６７イ∨Ｅ
従って、
（09）～（13）により、
（14）
（Ａ∪Ｂ）∩Ｃ＝（Ａ∩Ｃ）∪（Ｂ∩Ｃ）
といふ「集合の式」を、
（Ａ∨Ｂ）＆Ｃ⇔（Ａ＆Ｃ）∨（Ｂ＆Ｃ）
といふ「命題論理の式」は、「密接な類似性（close resemblance）」があるため、
（Ａ∪Ｂ）∩Ｃ＝（Ａ∩Ｃ）∪（Ｂ∩Ｃ）
といふ「等式（集合の分配法則）」を「証明」する際に、『ベン図』は「不要」である。
（16）
「数学」⇒「論理」⇒「集合」。
といふ「連想」からすると、
「集合論は、数学者によって、さぞかし重んじられてゐるのだらう。」
と思ってゐたものの、
（13）
（Ａ∪Ｂ）∩Ｃ＝（Ａ∩Ｃ）∪（Ｂ∩Ｃ）
といふ「集合の式」を、
（Ａ∨Ｂ）＆Ｃ⇔（Ａ＆Ｃ）∨（Ｂ＆Ｃ）
と書くと、「見た瞬間に、そんなの当然」である。
ｃｆ.
（ⅰ）
１ （１）（Ａ∨Ｂ）＆Ｃ 仮定
１ （２） Ａ∨Ｂ １＆Ｅ
１ （３） Ｃ １＆Ｅ
４ （４） Ａ 仮定
１４ （５） Ａ＆Ｃ ３４＆Ｉ
１４ （６）（Ａ＆Ｃ）∨（Ｂ＆Ｃ） ５∨Ｉ
７（７） Ｂ 仮定
１ ７（８） Ｂ＆Ｃ ３７＆Ｉ
１ ７（９）（Ａ＆Ｃ）∨（Ｂ＆Ｃ） ８∨Ｉ
１ （ア）（Ａ＆Ｃ）∨（Ｂ＆Ｃ） ２４６７９∨Ｅ
（ⅱ）
１ （１）（Ａ＆Ｃ）∨（Ｂ＆Ｃ） 仮定
２ （２）（Ａ＆Ｃ） 仮定
２ （３） Ａ ２＆Ｅ
２ （４） Ａ∨Ｂ ３∨Ｉ
２ （５） Ｃ ２＆Ｅ
２ （６）（Ａ∨Ｂ）＆Ｃ ４５＆Ｅ
７（７） Ｂ＆Ｃ 仮定
７（８） Ｂ ７＆Ｅ
７（９） Ａ∨Ｂ ８∨Ｉ
７（ア） Ｃ ７＆Ｅ
７（イ） （Ａ∨Ｂ）＆Ｃ ９ア＆Ｉ
１ （ウ）（Ａ∨Ｂ）＆Ｃ １２６７イ∨Ｅ
従って、
（09）～（13）により、
（14）
（Ａ∪Ｂ）∩Ｃ＝（Ａ∩Ｃ）∪（Ｂ∩Ｃ）
といふ「集合の式」を、
（Ａ∨Ｂ）＆Ｃ⇔（Ａ＆Ｃ）∨（Ｂ＆Ｃ）
といふ「命題論理の式」は、「密接な類似性（close resemblance）」があるため、
（Ａ∪Ｂ）∩Ｃ＝（Ａ∩Ｃ）∪（Ｂ∩Ｃ）
といふ「等式（集合の分配法則）」を「証明」する際に、『ベン図』は「不要」である。
（16）
「数学」⇒「論理」⇒「集合」。
といふ「連想」からすると、
「集合論は、数学者によって、さぞかし重んじられてゐるのだらう。」
と思ってゐたものの、
（謎の数学者【アメリカ大学准教授の数学チャンネル】）
とのことである。
（01）
練習２ Ａ⊆Ｂ⇔Ａ∪Ｂ＝Ｂ，また、Ａ⊆Ｂ⇔Ａ∩Ｂ＝Ａ を証明せよ。
（数研出版、チャート式 基礎からの確率・統計、初版 昭和４２年、１３頁）
然るに、
（02）
「練習略解」は「分かり難い」ため、
「命題計算」で『証明』することにした。
然るに、
（03）
（ⅰ）
１ （１） Ａ→Ｂ 仮定
２ （２） Ａ∨Ｂ 仮定
３ （３） Ａ 仮定
１ ３ （４） Ｂ １３ＭＰＰ
５ （５） Ｂ 仮定
１２ （６） Ｂ ２３４５５∨Ｅ
１ （７） Ａ∨Ｂ→Ｂ ２６ＣＰ
８（８） Ｂ Ａ
８（９） Ａ∨Ｂ ８∨Ｉ
（ア） Ｂ→Ａ∨Ｂ ８９ＣＰ
１ （イ）（Ａ∨Ｂ→Ｂ）＆
（Ｂ→Ａ∨Ｂ） ７ア＆Ｉ
１ （ウ） Ａ∨Ｂ⇔Ｂ イＤｆ.⇔
（ⅱ）
１ （１） Ａ∨Ｂ⇔Ｂ 仮定
１ （２）（Ａ∨Ｂ→Ｂ）＆
（Ｂ→Ａ∨Ｂ） １Ｄｆ.⇔
１ （３） Ａ∨Ｂ→Ｂ ２＆Ｅ
４ （４） Ａ 仮定
４ （５） Ａ∨Ｂ ４∨Ｉ
１４ （６） Ｂ ３５ＭＰＰ
１ （７） Ａ→Ｂ ４６ＣＰ
（ⅲ）
１ （１） Ａ→Ｂ 仮定
２ （２） Ａ＆Ｂ 仮定
２ （３） Ａ ２＆Ｅ
（４） Ａ＆Ｂ→Ａ ２３ＣＰ
５（５） Ａ Ａ
１ ５（６） Ｂ １５ＭＰＰ
１ ５（７） Ａ＆Ｂ ５６＆Ｉ
１ （８） Ａ→Ａ＆Ｂ ５７ＣＰ
１ （９）（Ａ＆Ｂ→Ａ）＆
（Ａ→Ａ＆Ｂ） ４８＆Ｉ
１ （ア） Ａ＆Ｂ⇔Ａ ９Ｄｆ．⇔
（ⅳ）
１ （１） Ａ＆Ｂ⇔Ａ Ａ
１ （２）（Ａ＆Ｂ→Ａ）＆
（Ａ→Ａ＆Ｂ） １Ｄｆ.⇔
１ （３） Ａ→Ａ＆Ｂ ２＆Ｅ
４（４） Ａ Ａ
１４（５） Ａ＆Ｂ ３４ＭＰＰ
１４（６） Ｂ ５＆Ｅ
１ （７） Ａ→Ｂ ４６ＣＰ
従って、
（03）により、
（04）
「命題論理」の「言葉（記号）」で書くと、
① Ａ→Ｂ
② Ａ∨Ｂ⇔Ｂ
③ Ａ→Ｂ
④ Ａ＆Ｂ⇔Ａ
に於いて、
①＝② であって、
③＝④ である。
従って、
（04）により、
（05）
「集合」の「言葉（記号）」で書くと、
① Ａ⊆Ｂ
② Ａ∪Ｂ＝Ｂ
③ Ａ∩Ｂ＝Ａ
に於いて、
①＝②＝③ である。
（01）
「すべてのフランス人は寛大である」は一種の条件文として適切に記号化されるので、これに同化してしまって、
「幾らかのフランス人は寛大である」を、正しく「∃ｘ（Ｆｘ＆Ｇｘ）」と記号化するかわりに、
「∃ｘ（Ｆｘ→Ｇｘ）」とするのは、よくある間違いである。しかし、「∃ｘ（Ｆｘ→Ｇｘ）」は、
「それがフランス人であるならば、寛大であるようなものが存在する」ことを主張するのであって、
「これは、かりにフランス人が存在しない」としても「真」であろう。しかるに、
「幾らかのフランス人は寛大である」はそうではない。
（E.j.レモン 著、竹尾治一郎・浅野楢英 訳、論理学初歩、1973年、１２３・１２４頁）
然るに、
（02）
１（１）～∃ｘ（Ｆｘ） Ａ
１（２）∀ｘ（～Ｆｘ） １量化子の関係
１（３） ～Ｆａ １ＵＥ
１（４）∃ｘ（～Ｆｘ） ２ＥＩ
１（５）∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ） ３∨Ｉ
従って、
（02）により、
（03）
① ～∃ｘ（Ｆｘ）├ ∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ）
といふ「連式」は「妥当」である。
然るに、
（04）
（ⅱ）
１ （１）∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ） Ａ
２ （２）∃ｘ（～Ｆｘ） Ａ
３ （３） ～Ｆａ Ａ
３ （４） ～Ｆａ∨Ｇａ ３∨Ｉ
３ （５） Ｆａ→Ｇａ ４含意の定義
３ （６） ∃ｘ（Ｆｘ→Ｇｘ） ３ＥＩ
２ （７） ∃ｘ（Ｆｘ→Ｇｘ） ２３６ＥＥ
８ （８） ∃ｘ（Ｇｘ） Ａ
９（９） Ｇａ Ａ
９（ア） ～Ｆａ∨Ｇａ ９∨Ｉ
９（イ） Ｆａ→Ｇａ ア含意の定義
９（ウ） ∃ｘ（Ｆｘ→Ｇｘ） イＥＩ
８ （エ） ∃ｘ（Ｆｘ→Ｇｘ） ８９ウＥＥ
１ （オ） ∃ｘ（Ｆｘ→Ｇｘ） １２７８エ∨Ｅ
（ⅲ）
１ （１） ∃ｘ（Ｆｘ→Ｇｘ） Ａ
２ （２） Ｆａ→Ｇａ Ａ
３ （３） ∀ｘ（Ｆｘ） Ａ
３ （４） Ｆａ ３ＵＥ
２３ （５） Ｇａ Ａ
２３ （６） ∃ｘ（Ｇｘ） ５ＥＩ
２ （７） ∀ｘ（Ｆｘ）→∃ｘ（Ｇｘ） ３６ＣＰ
２ （８）～∀ｘ（Ｆｘ）∨∃ｘ（Ｇｘ） ７含意の定義
９ （９）～∀ｘ（Ｆｘ） Ａ
９ （ア）∃ｘ（～Ｆｘ） ９含意の定義
９ （イ）∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ） ア∨Ｉ
ウ（ウ） ∃ｘ（Ｇｘ） Ａ
ウ（エ）∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ） ウ∨Ｉ
２ （オ）∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ） ２９イウエ∨Ｅ
１ （カ）∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ） １２オＥＥ
従って、
（04）により、
（05）
② ∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ）
③ ∃ｘ（Ｆｘ→Ｇｘ）
に於いて、
②＝③ である。
従って、
（03）（04）（05）により、
（06）
① ～∃ｘ（Ｆｘ）├ ∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ）
② ～∃ｘ（Ｆｘ）├ ∃ｘ（Ｆｘ→Ｇｘ）
に於いて、
①＝② であって、尚且つ、
① は「妥当」である。
従って、
（06）により、
（07）
① ～∃ｘ（Ｆｘ）├ ∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ）
② ～∃ｘ（Ｆｘ）├ ∃ｘ（Ｆｘ→Ｇｘ）
といふ「連式」は、両方とも「妥当」である。
従って、
（01）（07）により、
（08）
② ～∃ｘ（Ｆｘ）├ ∃ｘ（Ｆｘ→Ｇｘ）
といふ「連式」、すなはち、
② フランス人であるｘは存在しない。故に、∃ｘ（Ｆｘ→Ｇｘ）
といふ「連式」は、「妥当」である。
従って、
（01）（08）により、
（09）
「∃ｘ（Ｆｘ→Ｇｘ）」とするのは、よくある間違いである。しかし、「∃ｘ（Ｆｘ→Ｇｘ）」は、
「それがフランス人であるならば、寛大であるようなものが存在する」ことを主張するのであって、
「これは、かりにフランス人が存在しない」としても「真」であろう。
といふ、『E.J.レモンの説明』は、確かに、「正しい」。
然るに、
（10）
① ～∃ｘ（Ｆｘ）├ ∃ｘ（～Ｆｘ）∨∃ｘ（Ｇｘ）
② ～∃ｘ（Ｆｘ）├ ∃ｘ（Ｆｘ→Ｇｘ）
に於いて、
①＝② である。
といふことは、「述語論理」を学び始めたばかりの初学者には「理解できない」。
然るに、
（11）
「証明」とは、「相手にも分かるように、説明すること」である。
従って、
（02）～（11）により、
（12）
「∃ｘ（Ｆｘ→Ｇｘ）」に関する、
「以上のやうな説明」は、「証明」であるとは、言へない（！？）。