(01)
①ABC
②ACB
③BAC
④BCA
⑤CAB
⑥CBA
従って、
(01)により、
(02)
{A、B、C}から{3つを取り出して、並べた}際の「並べ方」は、
3P3=3!=3×2×1=6通り。
従って、
(02)により、
(03)
①ABC
②ACB
③BAC
④BCA
⑤CAB
⑥CBA
に対して、「ED」を加へた、
①ABCED
②ACBED
③BACED
④BCAED
⑤CABED
⑥CBAED
も、「6通り」である。
従って、
(03)により、
(04)
①ABC
②ACB
③BAC
④BCA
⑤CAB
⑥CBA
に対して、「DE」を加へた、
①ABCDE
②ACBDE
③BACDE
④BCADE
⑤CABDE
⑥CBADE
も、「6通り」である。
従って、
(03)(04)により、
(05)
①ABC
②ACB
③BAC
④BCA
⑤CAB
⑥CBA
に対して、「ED」、
または、 「DE」を加へた、
①ABCDE
②ABCED
③ACBDE
④ACBED
⑤BACDE
⑥BACED
⑦BCADE
⑧BCAED
⑨CABDE
⑩CABED
⑪CBADE
⑫CBAED
は、「6×2=12通り」である。
然るに、
(06)
{A、B、C、D、E}から{5つを取り出して、並べた}際の「並べ方」は、
「5P5=5!=5×4×3×2×1=120通り」である。
従って、
(05)(06)により、
(07)
{A、B、C、D、E}から{5つを取り出して、並べた}際の、
5P5=5!=5×4×3×2×1=120通り。
の中には、
①ABCDE
②ABCED
③ACBDE
④ACBED
⑤BACDE
⑥BACED
⑦BCADE
⑧BCAED
⑨CABDE
⑩CABED
⑪CBADE
⑫CBAED
といふ「6×2=12通り」が、含まれてゐる。
然るに、
(08)
ABCDE①
ABCED②
ABDCE
ABDEC
ABECD
ABEDC
ACBDE③
ACBED④
ACDBE
ACDEB
ACEBD
ACEDB
ADBCE
ADBEC
ADCBE
ADCEB
ADEBC
ADECB
AEBCD
AEBDC
AECBD
AECDB
AEDBC
AEDCB
BACDE⑤
BACED⑥
BADCE
BADEC
BAECD
BAEDC
BCADE⑦
BCAED⑧
BCDAE
BCDEA
BCEAD
BCEDA
BDACE
BDAEC
BDCAE
BDCEA
BDEAC
BDECA
BEACD
BEADC
BECAD
BECDA
BEDAC
BEDCA
CABDE⑨
CABED⑩
CADBE
CADEB
CAEBD
CAEDB
CBADE⑪
CBAED⑫
CBDAE
CBDEA
CBEAD
CBEDA
CDABE
CDAEB
CDBAE
CDBEA
CDEAB
CDEBA
CEABD
CEADB
CEBAD
CEBDA
CEDAB
CEDBA
DABCE
DABEC
DACBE
DACEB
DAEBC
DAECB
DBACE
DBAEC
DBCAE
DBCEA
DBEAC
DBECA
DCABE
DCAEB
DCBAE
DCBEA
DCEAB
DCEBA
DEABC
DEACB
DEBAC
DEBCA
DECAB
DECBA
EABCD
EABDC
EACBD
EACDB
EADBC
EADCB
EBACD
EBADC
EBCAD
EBCDA
EBDAC
EBDCA
ECABD
ECADB
ECBAD
ECBDA
ECDAB
ECDBA
EDABC
EDACB
EDBAC
EDBCA
EDCAB
EDCBA
従って、
(07)(08)により、
(09)
{A、B、C、D、E}から{5つを取り出して、並べた}際の、
5P5=5!=5×4×3×2×1=120通り。
の中には、実際に、
①ABCDE
②ABCED
③ACBDE
④ACBED
⑤BACDE
⑥BACED
⑦BCADE
⑧BCAED
⑨CABDE
⑩CABED
⑪CBADE
⑫CBAED
といふ「6×2=12通り」が、含まれてゐる。
従って、
(07)(08)(09)により、
(10)
{A、B、C、D、E}から{5つを取り出して、並べた}際の、
5P5=5!=5×4×3×2×1=120通り。
の中には、
①DECAB
②DECBA
③DCEAB
④DCEBA
⑤EDCAB
⑥EDCBA
⑦ECDAB
⑧ECDBA
⑨CDEAB
⑩CDEBA
⑪CEDAB
⑫CEDBA
といふ「6×2=12通り」が、含まれてゐる。
従って、
(09)(10)により、
(11)
{A、B、C、D、E}から、『ランダム』に、{5つを取り出して、並べた}際に、
{#、#、#、D、E}または、
{#、#、#、E、D}といふ「順番」で並ぶ「確率」は、
{(5-2)!×2!}÷5!=12÷120=0.1
である。
従って、
(11)により、
(12)
{A、B、C、D、E}や、
{ア、イ、ウ、エ、オ}を含む{41個の要素}から、『ランダム』に、{41個を取り出して、並べた}際に、
{#、#、・・・・・・・、ア、イ、ウ、エ、オ}や、
{#、#、・・・・・・・、オ、エ、ウ、イ、ア}といふ「順番」で並ぶ「確率」は、
{(41-5)!×5!}÷41!=(1÷749394)≒0.0000013344(約75万分の1)。
である。
従って、
(12)により、
(13)
{ア、イ、ウ、エ、オ}を含む{41個の要素}から、『ランダム』に、{41個を取り出して、並べた}際に、
{A、B、・・・・・・・、ア、イ、ウ、エ、オ}や、
{F、Q、・・・・・・・、ウ、エ、オ、ア、イ}や、
{R、Z、・・・・・・・、オ、エ、ウ、イ、ア}といふ「順番」で並ぶ「確率」は、 「0.00014%」にも、満たない。
従って、
(14)
{2018年1月26日、2019年1月04日、2019年1月11日、2019年1月18日、2019年1月29日}
を含む{41個の日付}から、『ランダム』に、{41個を取り出して、並べた}際に、
{#、#、・・・・、2018年1月26日、2019年1月04日、2019年1月11日、2019年1月18日、2019年1月29日}や、
{#、#、・・・・、2019年1月29日、2019年1月18日、2018年1月26日、2019年1月11日、2019年1月04日}といふ「順番」で並ぶ「確率」は、
「0.00014%」にも、満たない。
然るに、
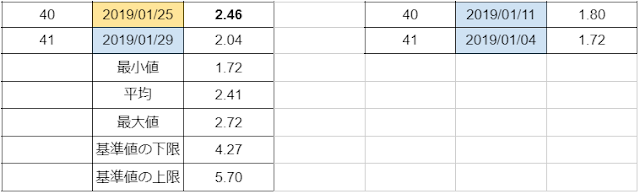
(15)
従って、
(14)(15)により、
(16)
「0.00014%」にも満たない、「確率」からすれば、
{2012年6月18日}から{2019年1月29日}までの、{41回の血液検査}に於いて、
{2018年1月26日、2019年1月04日、2019年1月11日、2019年1月18日、2019年1月29日}といふ{5回}だけが、
{点滴の最中}であって、尚且つ、
{2018年1月26日、2019年1月04日、2019年1月11日、2019年1月18日、2019年1月29日}といふ{5回}の{数値}が、
{大きい順}に並べた際に、
{37番目、38番目、39番目、40番目、41番目}
である。
といふことは、「単なる偶然」ではあり得ない。
然るに、
(17)
従って、
(19)により、
(20)
従って、
(19)により、
(20)
①「脱水」であるならば、(「点滴」をすれば、「数値は下降する」)。
という風に、鈴木医師は、述べてゐる。
然るに、
(21)
(ⅰ)
1 (1) P→(Q→ R) A
2 (2) Q&~R A
3(3) Q→ R A
2 (4) Q 2&E
23(5) R 34MPP
3(6) ~R 2&E
23(7) R&~R 56&I
2 (8) ~(Q→ R) 37RAA
12 (9)~P 18MTT
1 (ア)(Q&~R)→~P 29CP
(ⅱ)
1 (1) (Q&~R)→~P A
2 (2) P A
2 (3) ~~P 2DN
12 (4)~(Q&~R) 13MTT
5 (5) Q A
6(6) ~R A
56(7) Q&~R 56&I
1256(8)~(Q&~R)&
(Q&~R) 47&I
125 (9) ~~R 68RAA
125 (ア) R 9DN
12 (イ) Q→R 5アCP
1 (ウ)P→(Q→R) 2イCP
従って、
(21)により、
(22)
① P→(Q→R)
②(Q&~R)→~P
に於いて、
①=② は「対偶」である。
従って、
(22)により、
(23)
P=「脱水」である。
Q=「点滴」をする。
R=「数値は下降する」。
とするならば、
① 「脱水」であるならば、(「点滴」をすれば、「数値は下降する」)。
②(「点滴」をしても、「数値が下降しない」)のであれば、「脱水」ではない。
に於いて、 ①=② は、「対偶」である。
然るに、
(24)
2019年1月25日にかけての、『急性腎不全』の「原因」は「脱水」である。
(26)
出来れば、
といふ「教科書」で、『推計学』といふ「数学」を学んだ上で、「医療裁判」に臨みたいものの、『高校数学A』を理解するのがやっとである私には、そのやうなことをしてゐる、「時間的な余裕」はない。