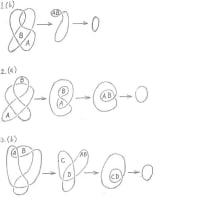今年11月13日のブログで言及したように、今年のノーベル物理学賞は、量子力学にトポロジー(位相幾何学)の概念を導入した米国の研究者に贈られた。
このニュースを伝える新聞記事によれば、「量子力学を記述する波動方程式にトポロジーを導入した」とし、トポロジーとは、「形や空間を連続的に変形させても保たれる性質のこと」とし、トポロジーによる物体の分類として、コップは穴の数がゼロ、ドーナツは一つ、メガネは二つなどと説明されていた。
波動方程式という数学的記述に、物体の形の分類方法を導入するとはどういうことか?このような説明では、専門家の間では通用したとしても、素人は全く理解できないであろう。
そこで、研究成果の概念を主体にして説明することにし、最後にこの概念と物体の分類としてのトポロジーとどう対応するのかについて言及することにした。
量子力学の波動方程式は、次のような形式をしている。
ハミルトニアン×波動関数=エネルギー×波動関数
ここで、ハミルトニアンは、系がもつ全エネルギーに対応し、各項が演算子から成る多項式である。エネルギーは、演算子の式に対してスカラーとも言われる通常の変数である。ハミルトニアンに適切な演算子の式を設定し、この方程式を解くと、解けた場合には、飛び飛びに並ぶエネルギー値と、各エネルギー値に対応する波動関数が得られる。
例えば、11月13日のブログで取り上げたバネ結合された質点のモデルについて、量子力学の波動方程式を用いて解くとどうなるか考える。すなわち、質点が原点Oからx軸方向にxだけずれたとき、バネによって質点に働く力-kxがポテンシャル(k/2)x^2から導かれるようなモデルである。質点にこのような運動を生じしめる作用子は、物理的なバネに限られるものではなく抽象的なモデルと考えてよいから、一般に調和振動子と呼ばれる。
調和振動子の波動方程式をつくり、これを解くと、そのエネルギー準位は、最低レベルの準位から始まって離散的かつ等間隔に並ぶ。各エネルギー準位は、単振動に伴う角振動数wという変数によって特徴づけられる。角振動数とは、2×パイ×振動数(周波数)のことである。また、各エネルギー準位に対応する波動関数は、古典力学の場合の解である単振動に比べて、かなり複雑な関数となる。
次に、2次元の絶縁体に磁場をかけたときの波動方程式をつくって解くとともに、絶縁体内の自由電子がどのように運動するかについて考察する。温度をパラメータとして変化させると、統計力学による取り扱いをしなければならないので、簡単のために、絶対零度にある非磁性の絶縁体を考える。
また、フェルミエネルギーというエネルギー準位のことを考慮しなければならない。結晶体に電子が存在する場所として、電子が原子的に存在する価電子帯と、自由電子として存在する伝導帯とがあり、伝導帯の方がエネルギー準位が高い。絶対零度では、フェルミエネルギーの準位より上のエネルギー準位には電子状態が存在せず、それより下のエネルギー準位に電子が詰め込まれる。従って、フェルミエネルギーより下の準位に存在する電子には、熱に起因する運動は生じないと考えられる。
x-y平面上に薄い板状の絶縁体を置き、z軸方向に一様な磁束密度Bの磁場をかけたときの波動方程式をつくり、解くとする。このとき、ハミルトニアンには磁場の強さBのパラメータをもつ項が加わることになる。
この方程式を解くと、そのエネルギー準位は、調和振動子のエネルギー準位に等価であり、角振動数wをサイクロトロン周波数wに置き換えただけであることを知る。また、各エネルギー準位に対応する波動関数は、調和振動子のそれに類似したものになることを知る。
磁場がないときに連続的なエネルギー準位であった2次元電子系は、磁場をかけることによってランダウ準位と呼ばれる離散的な準位に束ねられる。フェルミエネルギーがランダウ準位間にある場合には、それより上のエネルギー準位には電子が存在しない状態となり、「バンド絶縁体」と呼ばれる絶縁体となる。バンドとは、何らかの乱れのためにランダウ準位がそれを中心に幅をもった帯状になることを言うのであろう。
2次元電子系に磁場をかけると、電子はローレンツ力を受け、一般的にはxy平面内で円運動を行う。その振動数がサイクロトロン周波数である。ただし、絶縁体のエッジでは、電子は円運動の途中で境界にぶつかって反発するので、スキップしながらエッジに沿って移動すると考えられている。その結果として、エッジ状態にある電子は、絶縁体のエッジに沿って、磁場の向きによって時計回わり又は反時計回わりに一周することになる。これは外部から電場を印加せずに生じる電子の流れであり、「量子ホール効果」と呼ばれる。
サイクロトロン周波数wは磁場の強さBに比例するので、磁場を変化させると、ランダウ準位も変化することになる。
なお、仮にランダウ準位間のギャップ内に位置するエネルギー準位を指定すると、対応する波動関数は特異的になる。
詳しい説明は省略するが、2次元バンド絶縁体の各バンドに対してホール電流に関するホール伝導率を計算すると、そのバンドのチャーン数という数値に比例することが分かる。絶縁体全体のホール伝導率は、充填されているバンドのホール伝導率の総和になる。n番目のバンドに対応するチャーン数は必ず整数になることが証明される。ただし、注目しているn番目のバンドは他のバンドとバンドギャップで隔てられているとする。言い換えれば、2次元バンド絶縁体ではホール伝導率が必ず量子化するという整数量子ホール効果が導かれることになる。
磁場を変化させた場合にも、ホール伝導度、すなわちチャーン数は変化しない。さらに、一般的に、バンド間のギャップを閉じないように系のハミルトニアンを連続変形しても注目しているバンドのチャーン数は変化しない。それ故に、チャーン数はトポロジカル不変量と呼ばれるものの一つである。
2次元バンド絶縁体のz軸方向上向きに磁場をかけると、エッジには時計回りにホール電流が流れる。このとき、電流中の電子のスピンは磁場の方向に整列するため、上向きのスピンとなる。また、この絶縁体にz軸方向下向きに磁場をかけると、エッジには反時計回りにホール電流が流れる。これに関係する電子のスピンは磁場の方向に整列するため、下向きのスピンとなる。
そうすると、一枚の2次元絶縁体に上向きの磁場と、同時に同じ強さの下向きの磁場をかけたとき、理論上は、そのエッジには時計回りのホール電流と、反時計回りのホール電流とが同時に流れると考えられる。言い換えれば、外部から磁場を印加しない状態でも、エッジには上向きスピンと下向きスピンとが等量、逆向きに流れている状態であり、正味の電流はゼロであるが、スピン分裂のため、互いに逆向きのスピン流が生じている状態となる。このような絶縁体は、2次元トポロジカル絶縁体と呼ばれる。
2次元トポロジカル絶縁体のバルク(試料内部)では、価電子帯と伝導帯との間にはバルクのギャップと言われるギャップが開いているとし、そのギャップの中にフェルミエネルギーの準位があるとする。バルクとは異なり、同絶縁体のエッジは、ギャップレスと言われる特異的な状態となり、金属的な性質を示す。同じフェルミエネルギーの下で、エッジの伝導帯と価電子帯とが入れ替わる(バンド反転)のだろうか。
通常の絶縁体とトポロジカル絶縁体との電子素子としての違いは、絶縁体と半導体との違いから類推できる。例えばN型半導体では、結晶体に不純物を含ませることによって、ギャップの中に不純物による新たなエネルギー準位を設け、絶対零度より高い温度で不純物準位にある電子が伝導帯に移り、伝導性を示す。絶縁体のエッジがギャップレスになれば、価電子帯の電子は、低温度で伝導帯に移れるのであろう。
外部磁場がない場合でも、電子の運動によって磁場が発生するので、波動方程式のハミルトニアンには、発生する磁場の強さBのパラメータの項を加えなければならない。
通常の絶縁体と、トポロジカル絶縁体とは、互いに異なる相であり、バルクのギャップを閉じずにハミルトニアンを連続変形しても互いに移り変わることができない。
このような変形による分類を特徴づけるトポロジカル不変量が存在し、非磁性絶縁体では0、2次元トポロジカル絶縁体では1の値が与えられている。
物体の分類として、トポロジーで言う指数という不変量がある。例えばコップは穴の数がゼロであって、指数が2、ドーナツは穴の数が1であって、指数が0であり、連続変形によって互いに移り変わることができない。これは、上記トポロジカル不変量によって特徴づけられる通常の絶縁体と、トポロジカル絶縁体とに対応すると考えられる。バルクのギャップが開いている/閉じているの区別が物体の穴あり/穴なしに対応するのだろうか。
NHKの科学番組で、サイエンスライターの竹内薫さんの説明を聴いていて、次のような解釈もできるだろうと考えた。
細長い紙片の短い辺をつなぐと、単純な帯状のリングができる。このリングのおもて面という二次元空間に波動関数が存在するとすれば、リングをどう連続変形しても、この関数はうら面という別の空間に移動することはできない。つまり、おもて面とうら面との間にはギャップが存在することになる。
一方、細長い紙片を一回ひねってから短い辺をつなぐと、いわゆるメービウスの帯ができる。この帯は、単純リングとは異なる相となり、おもて面とうら面という区別がなくなる。この帯面の空間に波動関数が存在すれば、この帯をどう連続変形しても、この関数はおもて面とうら面の両方に同時に存在すると言える。つまり、波動関数はギャップレスの帯面に存在することになる。また、この波動関数は、竹内さんが言う「波がねじれた状態」となることが分かる。
参考文献
一般的な量子力学と統計力学の教科書のほかに、
斉藤英治ほか著「スピン流とトポロジカル絶縁体」(共立出版)
このニュースを伝える新聞記事によれば、「量子力学を記述する波動方程式にトポロジーを導入した」とし、トポロジーとは、「形や空間を連続的に変形させても保たれる性質のこと」とし、トポロジーによる物体の分類として、コップは穴の数がゼロ、ドーナツは一つ、メガネは二つなどと説明されていた。
波動方程式という数学的記述に、物体の形の分類方法を導入するとはどういうことか?このような説明では、専門家の間では通用したとしても、素人は全く理解できないであろう。
そこで、研究成果の概念を主体にして説明することにし、最後にこの概念と物体の分類としてのトポロジーとどう対応するのかについて言及することにした。
量子力学の波動方程式は、次のような形式をしている。
ハミルトニアン×波動関数=エネルギー×波動関数
ここで、ハミルトニアンは、系がもつ全エネルギーに対応し、各項が演算子から成る多項式である。エネルギーは、演算子の式に対してスカラーとも言われる通常の変数である。ハミルトニアンに適切な演算子の式を設定し、この方程式を解くと、解けた場合には、飛び飛びに並ぶエネルギー値と、各エネルギー値に対応する波動関数が得られる。
例えば、11月13日のブログで取り上げたバネ結合された質点のモデルについて、量子力学の波動方程式を用いて解くとどうなるか考える。すなわち、質点が原点Oからx軸方向にxだけずれたとき、バネによって質点に働く力-kxがポテンシャル(k/2)x^2から導かれるようなモデルである。質点にこのような運動を生じしめる作用子は、物理的なバネに限られるものではなく抽象的なモデルと考えてよいから、一般に調和振動子と呼ばれる。
調和振動子の波動方程式をつくり、これを解くと、そのエネルギー準位は、最低レベルの準位から始まって離散的かつ等間隔に並ぶ。各エネルギー準位は、単振動に伴う角振動数wという変数によって特徴づけられる。角振動数とは、2×パイ×振動数(周波数)のことである。また、各エネルギー準位に対応する波動関数は、古典力学の場合の解である単振動に比べて、かなり複雑な関数となる。
次に、2次元の絶縁体に磁場をかけたときの波動方程式をつくって解くとともに、絶縁体内の自由電子がどのように運動するかについて考察する。温度をパラメータとして変化させると、統計力学による取り扱いをしなければならないので、簡単のために、絶対零度にある非磁性の絶縁体を考える。
また、フェルミエネルギーというエネルギー準位のことを考慮しなければならない。結晶体に電子が存在する場所として、電子が原子的に存在する価電子帯と、自由電子として存在する伝導帯とがあり、伝導帯の方がエネルギー準位が高い。絶対零度では、フェルミエネルギーの準位より上のエネルギー準位には電子状態が存在せず、それより下のエネルギー準位に電子が詰め込まれる。従って、フェルミエネルギーより下の準位に存在する電子には、熱に起因する運動は生じないと考えられる。
x-y平面上に薄い板状の絶縁体を置き、z軸方向に一様な磁束密度Bの磁場をかけたときの波動方程式をつくり、解くとする。このとき、ハミルトニアンには磁場の強さBのパラメータをもつ項が加わることになる。
この方程式を解くと、そのエネルギー準位は、調和振動子のエネルギー準位に等価であり、角振動数wをサイクロトロン周波数wに置き換えただけであることを知る。また、各エネルギー準位に対応する波動関数は、調和振動子のそれに類似したものになることを知る。
磁場がないときに連続的なエネルギー準位であった2次元電子系は、磁場をかけることによってランダウ準位と呼ばれる離散的な準位に束ねられる。フェルミエネルギーがランダウ準位間にある場合には、それより上のエネルギー準位には電子が存在しない状態となり、「バンド絶縁体」と呼ばれる絶縁体となる。バンドとは、何らかの乱れのためにランダウ準位がそれを中心に幅をもった帯状になることを言うのであろう。
2次元電子系に磁場をかけると、電子はローレンツ力を受け、一般的にはxy平面内で円運動を行う。その振動数がサイクロトロン周波数である。ただし、絶縁体のエッジでは、電子は円運動の途中で境界にぶつかって反発するので、スキップしながらエッジに沿って移動すると考えられている。その結果として、エッジ状態にある電子は、絶縁体のエッジに沿って、磁場の向きによって時計回わり又は反時計回わりに一周することになる。これは外部から電場を印加せずに生じる電子の流れであり、「量子ホール効果」と呼ばれる。
サイクロトロン周波数wは磁場の強さBに比例するので、磁場を変化させると、ランダウ準位も変化することになる。
なお、仮にランダウ準位間のギャップ内に位置するエネルギー準位を指定すると、対応する波動関数は特異的になる。
詳しい説明は省略するが、2次元バンド絶縁体の各バンドに対してホール電流に関するホール伝導率を計算すると、そのバンドのチャーン数という数値に比例することが分かる。絶縁体全体のホール伝導率は、充填されているバンドのホール伝導率の総和になる。n番目のバンドに対応するチャーン数は必ず整数になることが証明される。ただし、注目しているn番目のバンドは他のバンドとバンドギャップで隔てられているとする。言い換えれば、2次元バンド絶縁体ではホール伝導率が必ず量子化するという整数量子ホール効果が導かれることになる。
磁場を変化させた場合にも、ホール伝導度、すなわちチャーン数は変化しない。さらに、一般的に、バンド間のギャップを閉じないように系のハミルトニアンを連続変形しても注目しているバンドのチャーン数は変化しない。それ故に、チャーン数はトポロジカル不変量と呼ばれるものの一つである。
2次元バンド絶縁体のz軸方向上向きに磁場をかけると、エッジには時計回りにホール電流が流れる。このとき、電流中の電子のスピンは磁場の方向に整列するため、上向きのスピンとなる。また、この絶縁体にz軸方向下向きに磁場をかけると、エッジには反時計回りにホール電流が流れる。これに関係する電子のスピンは磁場の方向に整列するため、下向きのスピンとなる。
そうすると、一枚の2次元絶縁体に上向きの磁場と、同時に同じ強さの下向きの磁場をかけたとき、理論上は、そのエッジには時計回りのホール電流と、反時計回りのホール電流とが同時に流れると考えられる。言い換えれば、外部から磁場を印加しない状態でも、エッジには上向きスピンと下向きスピンとが等量、逆向きに流れている状態であり、正味の電流はゼロであるが、スピン分裂のため、互いに逆向きのスピン流が生じている状態となる。このような絶縁体は、2次元トポロジカル絶縁体と呼ばれる。
2次元トポロジカル絶縁体のバルク(試料内部)では、価電子帯と伝導帯との間にはバルクのギャップと言われるギャップが開いているとし、そのギャップの中にフェルミエネルギーの準位があるとする。バルクとは異なり、同絶縁体のエッジは、ギャップレスと言われる特異的な状態となり、金属的な性質を示す。同じフェルミエネルギーの下で、エッジの伝導帯と価電子帯とが入れ替わる(バンド反転)のだろうか。
通常の絶縁体とトポロジカル絶縁体との電子素子としての違いは、絶縁体と半導体との違いから類推できる。例えばN型半導体では、結晶体に不純物を含ませることによって、ギャップの中に不純物による新たなエネルギー準位を設け、絶対零度より高い温度で不純物準位にある電子が伝導帯に移り、伝導性を示す。絶縁体のエッジがギャップレスになれば、価電子帯の電子は、低温度で伝導帯に移れるのであろう。
外部磁場がない場合でも、電子の運動によって磁場が発生するので、波動方程式のハミルトニアンには、発生する磁場の強さBのパラメータの項を加えなければならない。
通常の絶縁体と、トポロジカル絶縁体とは、互いに異なる相であり、バルクのギャップを閉じずにハミルトニアンを連続変形しても互いに移り変わることができない。
このような変形による分類を特徴づけるトポロジカル不変量が存在し、非磁性絶縁体では0、2次元トポロジカル絶縁体では1の値が与えられている。
物体の分類として、トポロジーで言う指数という不変量がある。例えばコップは穴の数がゼロであって、指数が2、ドーナツは穴の数が1であって、指数が0であり、連続変形によって互いに移り変わることができない。これは、上記トポロジカル不変量によって特徴づけられる通常の絶縁体と、トポロジカル絶縁体とに対応すると考えられる。バルクのギャップが開いている/閉じているの区別が物体の穴あり/穴なしに対応するのだろうか。
NHKの科学番組で、サイエンスライターの竹内薫さんの説明を聴いていて、次のような解釈もできるだろうと考えた。
細長い紙片の短い辺をつなぐと、単純な帯状のリングができる。このリングのおもて面という二次元空間に波動関数が存在するとすれば、リングをどう連続変形しても、この関数はうら面という別の空間に移動することはできない。つまり、おもて面とうら面との間にはギャップが存在することになる。
一方、細長い紙片を一回ひねってから短い辺をつなぐと、いわゆるメービウスの帯ができる。この帯は、単純リングとは異なる相となり、おもて面とうら面という区別がなくなる。この帯面の空間に波動関数が存在すれば、この帯をどう連続変形しても、この関数はおもて面とうら面の両方に同時に存在すると言える。つまり、波動関数はギャップレスの帯面に存在することになる。また、この波動関数は、竹内さんが言う「波がねじれた状態」となることが分かる。
参考文献
一般的な量子力学と統計力学の教科書のほかに、
斉藤英治ほか著「スピン流とトポロジカル絶縁体」(共立出版)