4 部分積分の公式
∫x³logxdx を計算する
積分を計算するさいに, たいへん便利な公式があります.
部分積分の公式とよばれる計算法です. まず, かんたんな例を使って説明することにしましょう.
つぎの積分を考えます.
∫x³logxdx
この積分はかんたんに求められそうにありません. そこで





部分積分の公式


5 むずかしい積分を計算する
部分積分の応用
部分積分の公式を使って, ふくざつな積分の計算をしてみましょう.
つぎの積分を計算しなさい.

解答


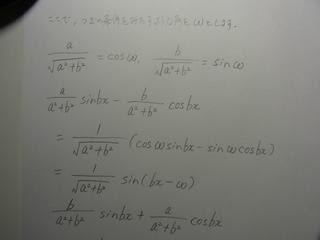

オイラーの公式との関係
上の計算は, オイラーの公式とよばれるつぎの関係式をつかうとかんたんにできます.

ここでx は実数, i は虚数単位です.
オイラーの公式については第8章でくわしくお話することにしますが, …… 『好きになる数学入門 第6巻 第2章』 宇沢弘文
と、ここで、私たちは、第8章に飛ぶ(笑)。
しかし、オイラーの説明が終わったら、すぐに戻るので、安心してほしい(笑)。
オイラーへ行く理由は、そこに、「フリードリッヒ大王」が出て来るからである。
連想はバッハへ繋がり、言葉はゲームのように、藤田弓子にも到達するであろう。
附録 『俳句の精神』 寺田寅彦
一例として「荒海や佐渡に横とう天の川」という句をとって考えてみる。西洋人流の科学的な態度から見た客観的写生的描写だと思って見れば、これは実につまらない短い記載的なセンテンスである。最も有利な見方をしても結局一枚の水彩画の内容の最も簡単なる説明書き以外の何物でもあり得ないであろう。それだのにこの句が多くの日本人にとって異常に美しい「詩」でありうるのはいったいどういうわけであろうか。この句の表面にはあらわな主観はきわめて希薄である。「横とう」という言葉にわずかな主観のにおいを感ずるくらいである。それだのにわれわれはこの句によって限り無き情緒の活動を喚起されるは何ゆえであろうか。
われわれにとっては「荒海」は単に航海学教科書におけるごとき波高く舟行に危険なる海面ではない。四面に海をめぐらす大八州国(おおやしまのくに)に数千年住み着いた民族の遠い祖先からの数限りもない海の幸いと海の禍い(わざわい)との記憶でいろどられた無始無終の絵巻物である。そうしてこの荒海は一面においてはわれわれの眼前に展開する客観の荒海でもあると同時にまたわれわれの頭脳を通してあらゆる過去の日本人の心にまで広がり連なる主観の荒海でもあるのである。「大海(おおうみ)に島もあらなくに海原(うなばら)のたゆとう波に立てる白雲」という万葉の歌に現れた「大海」の水はまた爾来千年の歳月を通してこの芭蕉翁の「荒海」とつながっているとも言われる。
もちろん西洋にも荒海とほぼ同義の言葉はある。またその言葉が多数の西洋人にいろいろの連想を呼び出す力をもっていることも事実である。しかしそれらの連想はおそらく多くは現実的功利的のものであろう。またもしそれが夢幻的空想的であるとしても、日本人のそれのように濃厚に圧縮されたそうして全国民に共通で固有な民族的記憶でいろどられたものではおそらくあり得ないであろうと思われる。
「佐渡」でも「天の川」でも同様である。いったいに俳句の季題と名づけられたあらゆる言葉がそうである。「春雨」「秋風」というような言葉は、日本人にとっては決して単なる気象学上の術語ではなくて、それぞれ莫大な空間と時間との間に広がる無限の事象とそれにつながる人間の肉体ならびに精神の活動の種々相を極度に圧縮し、煎じ詰めたエッセンスである。また、それらの言葉を耳に聞き目に見ることによって、その中に圧縮された内容を一度に呼び出し、出現させる呪文の役目をつとめるものである。そういう意味での「象徴」なのである。
こういう不思議な魔術がなかったとしたら俳句という十七字詩は畢竟(ひっきょう)ある無理解な西洋人の言ったようにそれぞれ一つの絵の題目のようなものになってしまう。
この魔術がどうして可能になったか、その理由はだいたい二つに分けて考えることができる。一つはすでに述べたとおり、日本人の自然観の特異性によるのである。ひと口に言えば自然の風物にわれわれの主観的生活を化合させ吸着(アドソープ)させて自然と人間との化合物ないし膠質物(こうしつぶつ)を作るという可能性である。これがなかったらこの魔術は無効である。しかしこれだけの理由ではまだ不十分である。もう一つの重大な理由と思われるのは日本古来の短い定型詩の存在とその流行によってこの上述の魔術に対するわれわれの感受性が養われて来たことである。換言すればわれわれが、長い修行によって「象徴国の国語」に習熟して来たせいである。 (昭和十年十月)

昭和36年版 『寺田寅彦全集 第12巻』
∫x³logxdx を計算する
積分を計算するさいに, たいへん便利な公式があります.
部分積分の公式とよばれる計算法です. まず, かんたんな例を使って説明することにしましょう.
つぎの積分を考えます.
∫x³logxdx
この積分はかんたんに求められそうにありません. そこで





部分積分の公式


5 むずかしい積分を計算する
部分積分の応用
部分積分の公式を使って, ふくざつな積分の計算をしてみましょう.
つぎの積分を計算しなさい.

解答


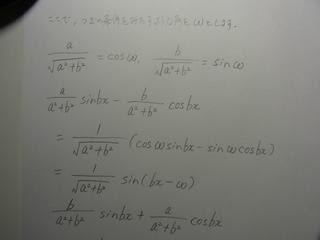

オイラーの公式との関係
上の計算は, オイラーの公式とよばれるつぎの関係式をつかうとかんたんにできます.

ここでx は実数, i は虚数単位です.
オイラーの公式については第8章でくわしくお話することにしますが, …… 『好きになる数学入門 第6巻 第2章』 宇沢弘文
と、ここで、私たちは、第8章に飛ぶ(笑)。
しかし、オイラーの説明が終わったら、すぐに戻るので、安心してほしい(笑)。
オイラーへ行く理由は、そこに、「フリードリッヒ大王」が出て来るからである。
連想はバッハへ繋がり、言葉はゲームのように、藤田弓子にも到達するであろう。
附録 『俳句の精神』 寺田寅彦
一例として「荒海や佐渡に横とう天の川」という句をとって考えてみる。西洋人流の科学的な態度から見た客観的写生的描写だと思って見れば、これは実につまらない短い記載的なセンテンスである。最も有利な見方をしても結局一枚の水彩画の内容の最も簡単なる説明書き以外の何物でもあり得ないであろう。それだのにこの句が多くの日本人にとって異常に美しい「詩」でありうるのはいったいどういうわけであろうか。この句の表面にはあらわな主観はきわめて希薄である。「横とう」という言葉にわずかな主観のにおいを感ずるくらいである。それだのにわれわれはこの句によって限り無き情緒の活動を喚起されるは何ゆえであろうか。
われわれにとっては「荒海」は単に航海学教科書におけるごとき波高く舟行に危険なる海面ではない。四面に海をめぐらす大八州国(おおやしまのくに)に数千年住み着いた民族の遠い祖先からの数限りもない海の幸いと海の禍い(わざわい)との記憶でいろどられた無始無終の絵巻物である。そうしてこの荒海は一面においてはわれわれの眼前に展開する客観の荒海でもあると同時にまたわれわれの頭脳を通してあらゆる過去の日本人の心にまで広がり連なる主観の荒海でもあるのである。「大海(おおうみ)に島もあらなくに海原(うなばら)のたゆとう波に立てる白雲」という万葉の歌に現れた「大海」の水はまた爾来千年の歳月を通してこの芭蕉翁の「荒海」とつながっているとも言われる。
もちろん西洋にも荒海とほぼ同義の言葉はある。またその言葉が多数の西洋人にいろいろの連想を呼び出す力をもっていることも事実である。しかしそれらの連想はおそらく多くは現実的功利的のものであろう。またもしそれが夢幻的空想的であるとしても、日本人のそれのように濃厚に圧縮されたそうして全国民に共通で固有な民族的記憶でいろどられたものではおそらくあり得ないであろうと思われる。
「佐渡」でも「天の川」でも同様である。いったいに俳句の季題と名づけられたあらゆる言葉がそうである。「春雨」「秋風」というような言葉は、日本人にとっては決して単なる気象学上の術語ではなくて、それぞれ莫大な空間と時間との間に広がる無限の事象とそれにつながる人間の肉体ならびに精神の活動の種々相を極度に圧縮し、煎じ詰めたエッセンスである。また、それらの言葉を耳に聞き目に見ることによって、その中に圧縮された内容を一度に呼び出し、出現させる呪文の役目をつとめるものである。そういう意味での「象徴」なのである。
こういう不思議な魔術がなかったとしたら俳句という十七字詩は畢竟(ひっきょう)ある無理解な西洋人の言ったようにそれぞれ一つの絵の題目のようなものになってしまう。
この魔術がどうして可能になったか、その理由はだいたい二つに分けて考えることができる。一つはすでに述べたとおり、日本人の自然観の特異性によるのである。ひと口に言えば自然の風物にわれわれの主観的生活を化合させ吸着(アドソープ)させて自然と人間との化合物ないし膠質物(こうしつぶつ)を作るという可能性である。これがなかったらこの魔術は無効である。しかしこれだけの理由ではまだ不十分である。もう一つの重大な理由と思われるのは日本古来の短い定型詩の存在とその流行によってこの上述の魔術に対するわれわれの感受性が養われて来たことである。換言すればわれわれが、長い修行によって「象徴国の国語」に習熟して来たせいである。 (昭和十年十月)

昭和36年版 『寺田寅彦全集 第12巻』














