一辺の長さが2の正方形の内部には半径1の単位円を内接できる。その円の面積はパイ×r^2=パイである。また一稜の長さが2の立方体の内部には半径1の単位球が内接できる。その球の体積は(4/3)×パイ×r^3=(4/3)パイである。
一般に一稜の長さが2のn次元立方体にちょうど収容できる単位n次元球体を考える。円はn=2、球はn=3である。
nが大きくなるに従って、立方体の中で球体が占める体積の割合は劇的に小さくなる。100次元空間では、球体は消滅したも同然で、それが占める割合は約1/10^70しかない。
一辺または一稜の長さがsのn立方体の体積はs^nである。r=1の単位球体を取り囲む立方体はs=2なので、その面積または体積は2^nであり、その値は4,8,16,32,…と続く。
n球体の体積を求めるための公式が知られている。その公式に従ってn球体の体積を計算すると、nが2~5では次元数の増大とともにn球体の体積は増大し、n=5でピークに達する。5次元を超えると、nが増加するに従って単位n球体の体積は減少する。参考文献によれば、n=20で約0.0258、n=100では10^-40に近い値になるという。
立方体が指数関数的に膨張するのと同時に、球体は微々たるものへと収縮する。100次元空間では、立方体の体積は1.3×10^30にまで増大するのに対して、球体は2.4×10^-40にまで収縮する。立方体の体積のうち球体が占める割合は1.9×10^-70である。
単位n球体がn立方体に内接するのであれば、直感的にはn立方体の体積の増大と歩調を合わせてn球体の体積も増大してしかるべきと思える。ところがそうはならないのである。
そこで、まずn球体は本当にn立方体に内接するのかどうかを確認する。
例えば、3次元球体についてその球面を表す方程式は、次のように表すことができる。なお球体の中心を原点にとっている。
x^2+y^2+z^2=1
そうすると、この球面は、次の式で表される6つの平面と6点で接触する。
x=-1,x=1;y=-1,y=1;z=-1,z=1
同様に、n次元球体についてその球面は次の方程式で表せる。
x1^2+x2^2+…+xn^2=1
そうすると、この球面は、次の式で表される2n個の(n-1)球体の中の平面と接点をもつことは間違いないので、これを内接と呼べない理由は見当たらない。
x1=-1,x1=1;x2=-1,x2=1;…;xn=-1,xn=1
次に、n次元球体の体積は、その半径rにどのように依存しているのかについて調べる。
20次元球体についてその球面は次の式で表せる。
x1^2+x2^2+…+xi^2+…+x20^2=1
仮にすべてのxiが同じ値であるとしたとき、20xi^2=1である。そうすると、xiは約0.2236と計算できる。
そうであれば、xiの絶対値であるABS(xi)<0.2236ならば任意のxiについて次の式が必ず成立するので、すべてのxiの組合せがこの球体に含まれる。
x1^2+x2^2+…+xi^2+…+x20^2<1
逆にABS(xi)>0.2236の条件を満たすどのようなxiの組合せについても
x1^2+x2^2+…+x20^2>1
となり、そのようなすべてのxiの座標値の集合は単位20次元球体には含まれない。
100次元球体についても同様である。100xi^2=1とすると、同じ値のxiについてxiは0.1と計算できるので、すべてのxiの絶対値<0.1であればこの空間の座標値(x1,x2,…,x100)はこの100次元球体に含まれる。
逆にすべてのxiがこの条件を満たさないようなxiの組合せは、この100次元球体に含まれない。
xiについての条件がない任意のxiの組合せについては、計算式
x1^2+x2^+…+x100^2
の期待値はこの式の値そのものである。多くのxiの組合せについてその値は1より大きくなり、単位n次元球体には含まれない。つまり、そのようなxiの組合せは、単位100次元球体の体積には寄与しない。
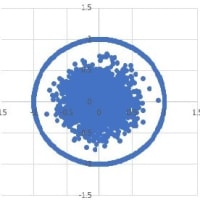
こうしてみると、高次元空間の単位球体の体積は球体の中心付近に集中する理由が分かる。
ここで、積分の技法を用いてn次元球体のうちn=3とn=4の場合の体積を計算してみる。
n=3の場合、球の方程式はf(x,y,z)=r^2であるから、x-y平面上に円をとり、z方向に円板の刻み幅dzをとる。円の半径はx-z平面上でx軸からの角度をt(シータ)とするとrcostであるから、円の面積はパイ×(rcost)^2となり、微小円板の体積はパイ×(rcost)^2×dzとなる。z=rsintであるからdz=rcostdtとすればよい。
そうすると、体積V3は、関数2×パイ×(rcost)^2×rcostdtをt=0からパイ/2まで積分したものになる。(cost)^3の積分公式を使って計算すると、V3=(4/3)×パイ×r^3を得る。
n=4の場合も同様であり、4次元球体の方程式はf(x,y,z,w)=r^2であるから、x-y-z平面(球平面)上に球をとり、w方向にこの球の平面領域の刻み幅dwをとる。この領域の半径はrcostであるから、球の体積は(4/3)×パイ×(rcost)^3となり、微小な4次元球体の体積は(4/3)×パイ×(rcost)^3×dwとなる。
そうすると、体積V4は、2×(4/3)×パイ×(rcost)^3×rcostdtをt=0からパイ/2まで積分したものになる。(cost)^4の積分公式を使って計算すると、V4=(1/2)×パイ^2×r^4を得る。
n=5,6,…についても同様である。一般に、n球体の体積は、次の漸化式が成り立つ。
n球体の体積=(n-2)球体の体積×2パイ×r^2/n
ところで、次元を越えて体積を比較することは実際に意味があるのかという問題がある。それぞれの次元にはそれ自体の測定単位(例えば平方メートルや立方メートル)が必要であり、したがってそれらの単位を伴う数の相対的な大きさにあまり意味はない。
ただ、それぞれの次元において体積比を考えることは意味があるのかも知れない。つまり、各次元においてn立方体の体積に対して、この立方体に内接する単位n球体の体積の割合を比較する場合である。それぞれの次元における体積は、その次元の標準的な体積を単位として測定するのであるから、それこそディメンション(次元)がそろっているというわけである。
それにしても、空間の次元が大きくなるに従って、ものを見つけることやその大きさや形状を測ることが難しくなる。数学者リチャード・ベルマンはこの現象を称して「次元の呪い」と名づけた。
参考文献
ブライアン・ヘイズ著「数学そぞろ歩き」(共立出版)
一般に一稜の長さが2のn次元立方体にちょうど収容できる単位n次元球体を考える。円はn=2、球はn=3である。
nが大きくなるに従って、立方体の中で球体が占める体積の割合は劇的に小さくなる。100次元空間では、球体は消滅したも同然で、それが占める割合は約1/10^70しかない。
一辺または一稜の長さがsのn立方体の体積はs^nである。r=1の単位球体を取り囲む立方体はs=2なので、その面積または体積は2^nであり、その値は4,8,16,32,…と続く。
n球体の体積を求めるための公式が知られている。その公式に従ってn球体の体積を計算すると、nが2~5では次元数の増大とともにn球体の体積は増大し、n=5でピークに達する。5次元を超えると、nが増加するに従って単位n球体の体積は減少する。参考文献によれば、n=20で約0.0258、n=100では10^-40に近い値になるという。
立方体が指数関数的に膨張するのと同時に、球体は微々たるものへと収縮する。100次元空間では、立方体の体積は1.3×10^30にまで増大するのに対して、球体は2.4×10^-40にまで収縮する。立方体の体積のうち球体が占める割合は1.9×10^-70である。
単位n球体がn立方体に内接するのであれば、直感的にはn立方体の体積の増大と歩調を合わせてn球体の体積も増大してしかるべきと思える。ところがそうはならないのである。
そこで、まずn球体は本当にn立方体に内接するのかどうかを確認する。
例えば、3次元球体についてその球面を表す方程式は、次のように表すことができる。なお球体の中心を原点にとっている。
x^2+y^2+z^2=1
そうすると、この球面は、次の式で表される6つの平面と6点で接触する。
x=-1,x=1;y=-1,y=1;z=-1,z=1
同様に、n次元球体についてその球面は次の方程式で表せる。
x1^2+x2^2+…+xn^2=1
そうすると、この球面は、次の式で表される2n個の(n-1)球体の中の平面と接点をもつことは間違いないので、これを内接と呼べない理由は見当たらない。
x1=-1,x1=1;x2=-1,x2=1;…;xn=-1,xn=1
次に、n次元球体の体積は、その半径rにどのように依存しているのかについて調べる。
20次元球体についてその球面は次の式で表せる。
x1^2+x2^2+…+xi^2+…+x20^2=1
仮にすべてのxiが同じ値であるとしたとき、20xi^2=1である。そうすると、xiは約0.2236と計算できる。
そうであれば、xiの絶対値であるABS(xi)<0.2236ならば任意のxiについて次の式が必ず成立するので、すべてのxiの組合せがこの球体に含まれる。
x1^2+x2^2+…+xi^2+…+x20^2<1
逆にABS(xi)>0.2236の条件を満たすどのようなxiの組合せについても
x1^2+x2^2+…+x20^2>1
となり、そのようなすべてのxiの座標値の集合は単位20次元球体には含まれない。
100次元球体についても同様である。100xi^2=1とすると、同じ値のxiについてxiは0.1と計算できるので、すべてのxiの絶対値<0.1であればこの空間の座標値(x1,x2,…,x100)はこの100次元球体に含まれる。
逆にすべてのxiがこの条件を満たさないようなxiの組合せは、この100次元球体に含まれない。
xiについての条件がない任意のxiの組合せについては、計算式
x1^2+x2^+…+x100^2
の期待値はこの式の値そのものである。多くのxiの組合せについてその値は1より大きくなり、単位n次元球体には含まれない。つまり、そのようなxiの組合せは、単位100次元球体の体積には寄与しない。
こうしてみると、高次元空間の単位球体の体積は球体の中心付近に集中する理由が分かる。
ここで、積分の技法を用いてn次元球体のうちn=3とn=4の場合の体積を計算してみる。
n=3の場合、球の方程式はf(x,y,z)=r^2であるから、x-y平面上に円をとり、z方向に円板の刻み幅dzをとる。円の半径はx-z平面上でx軸からの角度をt(シータ)とするとrcostであるから、円の面積はパイ×(rcost)^2となり、微小円板の体積はパイ×(rcost)^2×dzとなる。z=rsintであるからdz=rcostdtとすればよい。
そうすると、体積V3は、関数2×パイ×(rcost)^2×rcostdtをt=0からパイ/2まで積分したものになる。(cost)^3の積分公式を使って計算すると、V3=(4/3)×パイ×r^3を得る。
n=4の場合も同様であり、4次元球体の方程式はf(x,y,z,w)=r^2であるから、x-y-z平面(球平面)上に球をとり、w方向にこの球の平面領域の刻み幅dwをとる。この領域の半径はrcostであるから、球の体積は(4/3)×パイ×(rcost)^3となり、微小な4次元球体の体積は(4/3)×パイ×(rcost)^3×dwとなる。
そうすると、体積V4は、2×(4/3)×パイ×(rcost)^3×rcostdtをt=0からパイ/2まで積分したものになる。(cost)^4の積分公式を使って計算すると、V4=(1/2)×パイ^2×r^4を得る。
n=5,6,…についても同様である。一般に、n球体の体積は、次の漸化式が成り立つ。
n球体の体積=(n-2)球体の体積×2パイ×r^2/n
ところで、次元を越えて体積を比較することは実際に意味があるのかという問題がある。それぞれの次元にはそれ自体の測定単位(例えば平方メートルや立方メートル)が必要であり、したがってそれらの単位を伴う数の相対的な大きさにあまり意味はない。
ただ、それぞれの次元において体積比を考えることは意味があるのかも知れない。つまり、各次元においてn立方体の体積に対して、この立方体に内接する単位n球体の体積の割合を比較する場合である。それぞれの次元における体積は、その次元の標準的な体積を単位として測定するのであるから、それこそディメンション(次元)がそろっているというわけである。
それにしても、空間の次元が大きくなるに従って、ものを見つけることやその大きさや形状を測ることが難しくなる。数学者リチャード・ベルマンはこの現象を称して「次元の呪い」と名づけた。
参考文献
ブライアン・ヘイズ著「数学そぞろ歩き」(共立出版)












※コメント投稿者のブログIDはブログ作成者のみに通知されます