ナカナカピエロのうわのそら（情報量について）【改訂版】
以下の本が殊の外良かったので、自分が良かったなと思った情報量に関する事項を纏めておきたいと思う。
・社会科学のための ベイズ統計モデリング (統計ライブラリー) 浜田 宏
●情報量とは何か。
一般に場合の数、
について、以下の条件を満たす
関数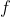
を情報量として定義する。
(1) = f(m) + f(n))
(2)
ならば %5Cleq f(m) )
(3) = 0)
これらの条件を満たす情報量の関数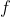として = K%5Clog(n) = -K%5Clog %5Cfrac{1}{n})
が定まる。（以下では
を仮定する。）
【証明】
場合の数を連続変数と仮定した場合の証明方法を記載します。
 = f(x) + f(y))
ここで)
とおくと
)=f(x + x%5Cepsilon) = f(x) + f(1 + %5Cepsilon))
)
を移行して、両辺を
で割ると、
 - f(x)}{x%5Cepsilon} = %5Cfrac{f(1 + %5Cepsilon)}{%5Cepsilon}%5Cfrac{1}{x})
を得る。
のとき、左辺は導関数の定義となり、
 = K%5Cfrac{1}{x})
ただし、/%5Cepsilon)
です。この両辺を積分することで、
 = K%5Clog x + C)
条件(3)から
。QED。
ここで導き出された情報量は確率の関数であり、具体的には確率の対数を取って符号を反転させた関数ともみなせる。
そこでより一般に（自己）情報量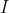
を確率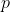
によって以下に定義する。
 = - %5Clog p)
確率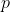が低いほど情報量が大きく、確率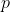が高いほど情報量は小さくなります。
●エントロピー
情報量の期待値のことをエントロピーと定義します。
確率密度関数が正において、連続確率変数
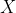のエントロピーを
 = H(f) = - %5Cint f(x)log f(x) dx)
と定義する。
●カルバックライブラー情報量
確率分布)
を基準にして)
がどれぐらい近いかの指標としてカルバックライブラー情報量があります。
 = %5Cint q(x) %5Clog %5Cfrac{q(x)}{p(x)} dx)
●交差エントロピー
確率分布, p(x))
について、交差エントロピーを
 = - %5Cint q(x)log p(x) dx)
と定義する。すると
 - D(q %5Cparallel p_2) = H_{q}(p_1) - H_{q}(p_2))
となり、交差エントロピーの差と等しくなる。よって交差エントロピーがデータから推定できれば、モデルの真の分布への相対的な近さを評価できる。
ここまでは一般的なお話。ここからベイズ統計の話をしたいのだが、以下のURLに書いてあるのでとりあえずここまで。
・渡辺澄夫 ベイズ統計の理論と方法
以下の本が殊の外良かったので、自分が良かったなと思った情報量に関する事項を纏めておきたいと思う。
・社会科学のための ベイズ統計モデリング (統計ライブラリー) 浜田 宏
●情報量とは何か。
一般に場合の数、
関数
(1)
(2)
(3)
これらの条件を満たす情報量の関数
【証明】
場合の数を連続変数と仮定した場合の証明方法を記載します。
ここで
を得る。
ただし、
条件(3)から
ここで導き出された情報量は確率の関数であり、具体的には確率の対数を取って符号を反転させた関数ともみなせる。
そこでより一般に（自己）情報量
確率
●エントロピー
情報量の期待値のことをエントロピーと定義します。
確率密度関数
と定義する。
●カルバックライブラー情報量
確率分布
●交差エントロピー
確率分布
と定義する。すると
となり、交差エントロピーの差と等しくなる。よって交差エントロピーがデータから推定できれば、モデルの真の分布への相対的な近さを評価できる。
ここまでは一般的なお話。ここからベイズ統計の話をしたいのだが、以下のURLに書いてあるのでとりあえずここまで。
・渡辺澄夫 ベイズ統計の理論と方法
