人間の脳に関する参考文献を読んで、長らく待たれていた脳機能の統一理論が提案されるようになったのかという感がある。
しかし、入門書と言ってもその内容は難解であり、自由エネルギー原理にしろ、その数学的記述にしろ、我々の認知機能と容易になじむものではない。
そこで、まず脳機能の統一原理の核になっている知覚モデルの部分を、主観的な説明になることは承知の上で、平易な言葉で語りたい。
知覚モデルについて、参考文献の文章を引用しながら説明する。網膜に映った画像をつくった原因は、直接知ることができないという意味で、「隠れ状態」と呼ばれる。これは「隠れた情報」という意味であり、「隠れた」とは、「分からない」という意味である。「状態」と呼ぶのは、熱力学で脳の内部エネルギーからそのエントロピーが決まり、エントロピーから状態が決まり、状態が情報に対応するためである。
以下は、参考文献からの引用である。「脳の仕事は、(網膜など感覚器官から入力された)感覚信号sから隠れ状態uを推論することである。この推論を行うため、とりあえず、頭の中で隠れ状態uの想定u0を定めて、それに基づいて予測信号g(u0)を計算する(注:g(u)はuの関数である)。実際に観測された感覚信号sとこの予測信号とのずれs-g(u0)が予測誤差信号である。脳はこの予測誤差信号が小さくなるように推定内容をu0からu1に更新する。次に、更新した想定u1に基づいて予測信号g(u1)を計算して再び予測誤差信号s-g(u1)を求め、これが小さくなるように推定内容をu2に更新する。この作業を繰り返し行うと、最終的な推定内容が求められる。」
感覚信号を大量に集めると、例えば新聞、テレビ、インターネット、文献などの情報源から入力した情報となる。このような情報はファクトと呼ばれる。脳は、少なくとも読解するための辞書を備えていて、入力された情報の意味を解釈する必要がある。
しかし、ファクトだけでは、パズルを解いたり、ゲームをしたり、家事をしたり、将来の予測をしたり、新しい製品をデザインするには不充分である。ファクトに加えてイマジネーションがどうしても必要になる。ファクトがマクロな形に整理された感覚信号であるとすれば、イマジネーションは、隠れ状態に相当するモデルを形成するためのマクロな予測信号ということになる。
そうすると、人は、推論によってイマジネーションと現実のファクトのギャップができるだけ小さくなるように両者を整合させていることになる。
イマジネーションに乏しいと、現在および過去のファクトに拘泥することになり、命令されたことしかやらない人間、前例を破るような新しい企画を立案できない人間、弱い立場の人の気持を想像できない人間、自分の過去の成功例を繰り返し語る人間などをつくることになる。逆に、イマジネーションが大き過ぎると、現実から遊離することになり、立案した計画が失敗したり、誰も利用しない発明品を作ったりすることになる。
知覚モデルの説明に戻り、状態uと信号sが一致するという理想的な場合には、s=g(u0)となるから、予測誤差が生じることなく、脳は信号sを認知できる。
ここでベイズの定理を用いて認知結果が正しいものとみなせる確率について考察する(一般的には関数の形をした確率分布であり、定数の確率も含めて「確率」と呼ぶ)。ベイズの定理は、事後確率=事前確率×条件付き確率と表せる。事前確率は、まだ結果がない状態の確率であり、p(u)と表せる。条件付き確率は、信号sが生じたという条件の下で、状態(原因)uによって信号sが生じる確率であり、p(s|u)と表せる。事後確率は、出た結果に基づく確率、あるいは信号sによって原因uが生じる確率であり、p(u|s)と表せる。
そうすると、p(u)×p(s|u)は事後確率に相当するが、仮にu=sとすれば、p(u)=p(s)であり、ともに確率1.0ということになる。また、原因と結果をとり替えても構わないから、p(u|s)=p(s|u)が成り立つ。従って、p(u)×p(s|u)=p(s)×p(u|s)が成り立つから、一般に事後確率p(u|s)は、次の式で表せる。
p(u|s)=p(u)×p(s|u)/p(s)
確率1.0の場合にしか成り立たない式を確率的に扱うと、1.0以外の確率の場合にも成り立ってしまうのだから面白い。
最初に状態uと信号sが一致しない場合には、sとg(u0)が一致しないから、状態uの候補をu1,u2,…のように変更するか、視点を変えるなどして信号sの入力条件を変更して新しいsを入力し直し、事後確率の計算を繰り返す。自分の身体を動かすことによって予測された感覚信号を再度観察すると、生起確率の高い感覚信号が得られる。このような推論は、「能動的推論」と呼ばれる。これは、予測する信号を確認する機能であるともいえる。
p(u0|s)
p(u1|s)=p(u0)×p(s|u1)/p(s)
と表現できる。ここでは、u0の結果が存在するから、p(u0)=p(u0|s)である。P(s|u0)は存在しない。信号sが変わらないので、p(s)は定数となる。
上記の知覚モデルでは、原因と結果をとり替えても構わないし、状態uの候補をu1,u2,…のように変更してもよいし、信号sについてもs1,s2,…のように事後確率を高めるために別の選択肢を選んでもよいのであった。そうであれば、イマジネーションのモデルにおいても、イマジネーションの候補I1,I2,…からどの候補を選択してもよい。定式化すれば、
p(I|f)=p(I)×p(f|I)/p(f)
で定められる事後確率を最大にするようなIとfの組(I,f)を選択すればよいのである。
さらに言えば、現実のファクトの代わりに理想とするイマジネーションのモデルを固定し、想起するイマジネーションの候補の中からギャップの小さな候補を選択してもよい。
脳機能は、リアルなパートとイマジナリーなパートから構成されていることをみても、自然は、複素数によって記述されねばならないことを示唆しているように思える。
脳機能をシミュレーションするような場合に、真の事後確率を直接的に計算して求めることは一般に困難である。そこで、事後確率を求める代わりにこれに近似する別の量である「認識確率」を計算する。脳は、事後確率を求める代わりに認識確率を計算していると考える。事後確率p(u|s)が知られないのであれば、その大小関係を知ることはできない。そうすると、p(u0|s)
そうであれば、脳は、予測誤差信号が小さくなるように、すなわち認識確率を大きくする方向で推論していると考えてよい。認識確率と真の事後確率(最終的な事後確率と言ってもよい)の差の絶対値をダイバージェンスと呼んでいる。この用語を用いるならば、脳は、ダイバージェンスを最小化するような認識確率を求めるように推論していると言ってもよい。
なお、ベイズ推論において、事前確率を認識確率で近似し、この認識確率と事後確率の差の絶対値をダイバージェンスとしてもよい。
参考文献の著者は、「自由エネルギー原理(注:脳の統一原理)は概念的なものではなく、数式を使って具体的に記述されたもので、ニューラルネットワークでの処理として表すことが可能です。」と言っている。引き続き、知覚モデルをニューラルネットワークでの処理として表し、その動作をシミュレーションしたい。
参考文献
乾敏郎など著「脳の大統一理論」(岩波科学ライブラリー)
しかし、入門書と言ってもその内容は難解であり、自由エネルギー原理にしろ、その数学的記述にしろ、我々の認知機能と容易になじむものではない。
そこで、まず脳機能の統一原理の核になっている知覚モデルの部分を、主観的な説明になることは承知の上で、平易な言葉で語りたい。
知覚モデルについて、参考文献の文章を引用しながら説明する。網膜に映った画像をつくった原因は、直接知ることができないという意味で、「隠れ状態」と呼ばれる。これは「隠れた情報」という意味であり、「隠れた」とは、「分からない」という意味である。「状態」と呼ぶのは、熱力学で脳の内部エネルギーからそのエントロピーが決まり、エントロピーから状態が決まり、状態が情報に対応するためである。
以下は、参考文献からの引用である。「脳の仕事は、(網膜など感覚器官から入力された)感覚信号sから隠れ状態uを推論することである。この推論を行うため、とりあえず、頭の中で隠れ状態uの想定u0を定めて、それに基づいて予測信号g(u0)を計算する(注:g(u)はuの関数である)。実際に観測された感覚信号sとこの予測信号とのずれs-g(u0)が予測誤差信号である。脳はこの予測誤差信号が小さくなるように推定内容をu0からu1に更新する。次に、更新した想定u1に基づいて予測信号g(u1)を計算して再び予測誤差信号s-g(u1)を求め、これが小さくなるように推定内容をu2に更新する。この作業を繰り返し行うと、最終的な推定内容が求められる。」
感覚信号を大量に集めると、例えば新聞、テレビ、インターネット、文献などの情報源から入力した情報となる。このような情報はファクトと呼ばれる。脳は、少なくとも読解するための辞書を備えていて、入力された情報の意味を解釈する必要がある。
しかし、ファクトだけでは、パズルを解いたり、ゲームをしたり、家事をしたり、将来の予測をしたり、新しい製品をデザインするには不充分である。ファクトに加えてイマジネーションがどうしても必要になる。ファクトがマクロな形に整理された感覚信号であるとすれば、イマジネーションは、隠れ状態に相当するモデルを形成するためのマクロな予測信号ということになる。
そうすると、人は、推論によってイマジネーションと現実のファクトのギャップができるだけ小さくなるように両者を整合させていることになる。
イマジネーションに乏しいと、現在および過去のファクトに拘泥することになり、命令されたことしかやらない人間、前例を破るような新しい企画を立案できない人間、弱い立場の人の気持を想像できない人間、自分の過去の成功例を繰り返し語る人間などをつくることになる。逆に、イマジネーションが大き過ぎると、現実から遊離することになり、立案した計画が失敗したり、誰も利用しない発明品を作ったりすることになる。
知覚モデルの説明に戻り、状態uと信号sが一致するという理想的な場合には、s=g(u0)となるから、予測誤差が生じることなく、脳は信号sを認知できる。
ここでベイズの定理を用いて認知結果が正しいものとみなせる確率について考察する(一般的には関数の形をした確率分布であり、定数の確率も含めて「確率」と呼ぶ)。ベイズの定理は、事後確率=事前確率×条件付き確率と表せる。事前確率は、まだ結果がない状態の確率であり、p(u)と表せる。条件付き確率は、信号sが生じたという条件の下で、状態(原因)uによって信号sが生じる確率であり、p(s|u)と表せる。事後確率は、出た結果に基づく確率、あるいは信号sによって原因uが生じる確率であり、p(u|s)と表せる。
そうすると、p(u)×p(s|u)は事後確率に相当するが、仮にu=sとすれば、p(u)=p(s)であり、ともに確率1.0ということになる。また、原因と結果をとり替えても構わないから、p(u|s)=p(s|u)が成り立つ。従って、p(u)×p(s|u)=p(s)×p(u|s)が成り立つから、一般に事後確率p(u|s)は、次の式で表せる。
p(u|s)=p(u)×p(s|u)/p(s)
確率1.0の場合にしか成り立たない式を確率的に扱うと、1.0以外の確率の場合にも成り立ってしまうのだから面白い。
最初に状態uと信号sが一致しない場合には、sとg(u0)が一致しないから、状態uの候補をu1,u2,…のように変更するか、視点を変えるなどして信号sの入力条件を変更して新しいsを入力し直し、事後確率の計算を繰り返す。自分の身体を動かすことによって予測された感覚信号を再度観察すると、生起確率の高い感覚信号が得られる。このような推論は、「能動的推論」と呼ばれる。これは、予測する信号を確認する機能であるともいえる。
p(u0|s)
と表現できる。ここでは、u0の結果が存在するから、p(u0)=p(u0|s)である。P(s|u0)は存在しない。信号sが変わらないので、p(s)は定数となる。
上記の知覚モデルでは、原因と結果をとり替えても構わないし、状態uの候補をu1,u2,…のように変更してもよいし、信号sについてもs1,s2,…のように事後確率を高めるために別の選択肢を選んでもよいのであった。そうであれば、イマジネーションのモデルにおいても、イマジネーションの候補I1,I2,…からどの候補を選択してもよい。定式化すれば、
p(I|f)=p(I)×p(f|I)/p(f)
で定められる事後確率を最大にするようなIとfの組(I,f)を選択すればよいのである。
さらに言えば、現実のファクトの代わりに理想とするイマジネーションのモデルを固定し、想起するイマジネーションの候補の中からギャップの小さな候補を選択してもよい。
脳機能は、リアルなパートとイマジナリーなパートから構成されていることをみても、自然は、複素数によって記述されねばならないことを示唆しているように思える。
脳機能をシミュレーションするような場合に、真の事後確率を直接的に計算して求めることは一般に困難である。そこで、事後確率を求める代わりにこれに近似する別の量である「認識確率」を計算する。脳は、事後確率を求める代わりに認識確率を計算していると考える。事後確率p(u|s)が知られないのであれば、その大小関係を知ることはできない。そうすると、p(u0|s)
そうであれば、脳は、予測誤差信号が小さくなるように、すなわち認識確率を大きくする方向で推論していると考えてよい。認識確率と真の事後確率(最終的な事後確率と言ってもよい)の差の絶対値をダイバージェンスと呼んでいる。この用語を用いるならば、脳は、ダイバージェンスを最小化するような認識確率を求めるように推論していると言ってもよい。
なお、ベイズ推論において、事前確率を認識確率で近似し、この認識確率と事後確率の差の絶対値をダイバージェンスとしてもよい。
参考文献の著者は、「自由エネルギー原理(注:脳の統一原理)は概念的なものではなく、数式を使って具体的に記述されたもので、ニューラルネットワークでの処理として表すことが可能です。」と言っている。引き続き、知覚モデルをニューラルネットワークでの処理として表し、その動作をシミュレーションしたい。
参考文献
乾敏郎など著「脳の大統一理論」(岩波科学ライブラリー)










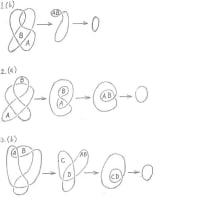


※コメント投稿者のブログIDはブログ作成者のみに通知されます