2018年12月2日付のブログで、単純な「平均顔」の画像をデザインし、いくつかの特徴領域のカテゴリを選択し、各特徴領域のデータをランダム化して、多数の変形顔の画像をつくることに言及した。
変形顔の輪郭は、ランダム・データに基づいているので折れ線となるであろう。この折れ線をなめらかな曲線に変えたいという欲求が生じる。
そこで、スプラインという技法を学んで、設定されたデータ点をなめらかな曲線で補間する技術を習得することにした。
スプライン技法によれば、目的とする曲線は、Bスプラインと呼ばれる基底関数にその係数を掛けたものの線形結合で表現される。この基底は、少なくとも一つの多項式片を連結したもので表される。2次曲線ならば3個までの2次式片を連結したもの、3次曲線ならば4個までの3次式片を連結したものとなる。
つまり、スプラインによって表現される曲線は、3層の階層構成をもつアーキテクチャとなっているのである。分かってくると、このアーキテクチャの華麗さとでも言えるものに魅了される。スプライン補間するための計算の手間は半端ではないが、定型計算をライブラリ化したり、数学ツールを使うことによって、その手間を軽減できるであろう。
基底となるBスプラインは、Nr,i(x)と表される。rは階数と呼ばれ、次数+1となる数である。iはその階数に属するBスプラインの番号を表している。
例えば、r=2(1次)のBスプラインN2,i(x)は、x軸上のxi-2=<x<xi,xi-2<xi-1<xiの区間に存在し、次の式で表される。
N2,i(x)=(x-xi-2)/(xi-1-xi-2)+(xi-x)/(xi-xi-1)
N2,i(x)は、xi-2=<x<xi-1にある第1項の1次式と区間xi-1=<x<xiにある第2項の1次式とを連結したものである。x<xi-2,x=>xiの区間ではN2,i(x)=0になる。xi-2,xi-1,xiを節点という。
N2,i-1(x)とは、N2,i(x)のiをi-1に変えたものであり、N2,i(x)の存在区間を左方向にシフトしたものであり、次の式で表される。
N2,i-1(x)=(x-xi-3)/(xi-2-xi-3)+(xi-1-x)/(xi-1-xi-2)
x<xi-3,x=>xi-1の区間ではN2,i-1(x)=0になる。
N3,i(x)は2次のBスプラインであり、次の漸化式で定義される。
N3,i(x)=(x-xi-3)N2,i-1(x)/(xi-1-xi-3)+(xi-x)N2,i(x)/(xi-xi-2)
N3,i(x)は、4つの2次式で構成されるが、区間xi-2=<x<xi-1に存在する2つの2次式は加算によって1つの2次式にまとまる。従って、N3,i(x)は、3つの2次式を連結したものとなる。x<xi-3,x=>xiの区間ではN3,i(x)=0になる。
この漸化式を用いると、関数N3,i(x)は、x=xi-2およびx=xi-1において関数値と一次微分係数が連続な曲線になることが確かめられる。
N4,i(x)など高次階のNr,i(x)も同様の漸化式で定義されるが、詳細は省略する。
N3,i(x)のxi-3をxi-2の方向に移動させ、xi-3=xi-2と重ねると、両節点は多重化される。こうすると、区間xi-1=<x<xiにある第3の2次式は変わらないが、区間xi-3=xi-2=<x<xi-1の第2の2次式は更新される。
更新された第2の2次式をy=ax^2+bx+cとすると、「x=xi-2のときy=0;x=xi-1のときyは正規化条件から決まる関数値;x=xi-1のときの一次微分係数が第3の2次式の同係数に一致」の3条件からa,b,cが求められる。これによってN3,i(x)は2つの2次式を連結したものに更新される。なお、第2の条件によって、x=xi-1のときの関数値は、第3の2次式の関数値に一致することが要請される。
同様に、N3,i(x)のxiをxi-1の方向に移動させ、節点xi-1=xiのように多重化したときも、区間xi-3=<x<xi-2の第1の2次式は変わらないが、区間xi-2=<x<xi-1=xiの第2の2次式は更新される。
同様に、N3,i(x)のxi-1,xi-2,xi-3をxi-1=xi-2=xi-3のように三重節点とすると、N3,i(x)の第3の2次式のみが更新されて残る。更新された第3の2次式をy=a(x-xi)^2とすると、x=xiのときy=0であるから、x=xi-1のときa(xi-1-xi)^2=1の正規化条件からaが求められる。N3,i(x)のxi,xi-1,xi-2を三重節点とする場合も同様の類推でy=a(x-xi-3)^2が決まる。
N3,i(x)に関し、x軸上の節点をx-2=x-1=x0=<x1<x2<...<xn=<xn+1=xn+2=xn+3とするとき、区間[x0,xn+1]において、2次のスプラインS(x)は2次のBスプラインの線形結合として表され、
S(x)=c1N3,1(x)+c2N3,2(x)+...+cn+3N3,n+3(x)
となる。nは多重節点以外にこの区間の内部に配置する節点の数である。ciは、Bスプライン係数である。
データ(Xj,Yj)(j=1,2,...,N)が与えられているとき、このデータをスプラインで補間する場合には、補間条件
S(Xj)=Yj
によってBスプライン係数ciを決定する。ここで、データの数(N)はパラメータの数n+3に一致させる必要がある。
Bスプラインの局所性により、区間[x0,xn+1]内の[x0,x1]など各小区間には3個のN3,i(x)のみが実際の計算に関与する。
例として、n=3とし、x0=0,x1=1,x2=2,x3=3,x4=4とする。X1=0,X2=0.5,X3=1.5,X4=2.5,X5=3.5,X6=4と設定すると、c1=Y1,c6=Y6が決定する。
残りのc2~c5を決定するためのS(Xj)に関する連立方程式は次の通りである。
c1N3,1(X2)+c3N3,3(X2)+c5N3,5(X2)=Y2
c2N3,2(X3)+c3N3,3(X3)+c5N3,5(X3)=Y3
c2N3,2(X4)+c4N3,4(X4)+c5N3,5(X4)=Y4
c2N3,2(X5)+c4N3,4(X5)+c6N3,6(X5)=Y5
ここで、N3,1(x)は(0,1);(1,0)を境界とする三重節点をもつBスプライン、N3,2(x)は(1,0);(4,0)を境界とする3連のBスプライン、N3,3(x)は(0,0);(2,0)を境界とする2連、N3,4(x)は(2,0);(4,0)を境界とする2連、N3,5(x)は(0,0);(3,0)を境界とする3連のBスプライン、N3,6(x)は(3,0);(4,0)を境界とする三重節点をもつBスプラインである。
例えば、小区間[1,2]において、N3,2(x)+N3,3(x)+N3,5(x)=1であることが確かめられる。すなわち、区間[0,4]においてN3,1(x)+...+N3,6(x)=1に正規化されていることを知る。
この方程式を解いてc2~c5が求められたら、各小区間について上式のXjの代わりにxの刻みを代入してyの値を計算する。
当然のことながら、S(x=Xj)=Yjとならなければならないから、この計算は、c2~c5の計算過程およびN3,1(x)~N3,6(x)の計算式のチェックにもなる。
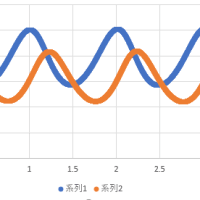
下図は、Y1=2.1,Y2=2.3,Y3=1.9,Y4=1.7,Y5=2.4,Y6=2.6と設定し、Excelを用いてy=S(x)を計算し、グラフ表示したものである。

(X1,Y1)~(X6,Y6)をマーカー表示とし、スプライン補間した部分と区別した方が分かりやすくなるが、一部のデータ点(Xj,Yj)のみをマーカー表示する方法が見当たらないので、すべてのデータについてマーカー表示なしとした。
参考文献
吉本富士市著「インターネット時代の数学―スプライン」(共立出版)
変形顔の輪郭は、ランダム・データに基づいているので折れ線となるであろう。この折れ線をなめらかな曲線に変えたいという欲求が生じる。
そこで、スプラインという技法を学んで、設定されたデータ点をなめらかな曲線で補間する技術を習得することにした。
スプライン技法によれば、目的とする曲線は、Bスプラインと呼ばれる基底関数にその係数を掛けたものの線形結合で表現される。この基底は、少なくとも一つの多項式片を連結したもので表される。2次曲線ならば3個までの2次式片を連結したもの、3次曲線ならば4個までの3次式片を連結したものとなる。
つまり、スプラインによって表現される曲線は、3層の階層構成をもつアーキテクチャとなっているのである。分かってくると、このアーキテクチャの華麗さとでも言えるものに魅了される。スプライン補間するための計算の手間は半端ではないが、定型計算をライブラリ化したり、数学ツールを使うことによって、その手間を軽減できるであろう。
基底となるBスプラインは、Nr,i(x)と表される。rは階数と呼ばれ、次数+1となる数である。iはその階数に属するBスプラインの番号を表している。
例えば、r=2(1次)のBスプラインN2,i(x)は、x軸上のxi-2=<x<xi,xi-2<xi-1<xiの区間に存在し、次の式で表される。
N2,i(x)=(x-xi-2)/(xi-1-xi-2)+(xi-x)/(xi-xi-1)
N2,i(x)は、xi-2=<x<xi-1にある第1項の1次式と区間xi-1=<x<xiにある第2項の1次式とを連結したものである。x<xi-2,x=>xiの区間ではN2,i(x)=0になる。xi-2,xi-1,xiを節点という。
N2,i-1(x)とは、N2,i(x)のiをi-1に変えたものであり、N2,i(x)の存在区間を左方向にシフトしたものであり、次の式で表される。
N2,i-1(x)=(x-xi-3)/(xi-2-xi-3)+(xi-1-x)/(xi-1-xi-2)
x<xi-3,x=>xi-1の区間ではN2,i-1(x)=0になる。
N3,i(x)は2次のBスプラインであり、次の漸化式で定義される。
N3,i(x)=(x-xi-3)N2,i-1(x)/(xi-1-xi-3)+(xi-x)N2,i(x)/(xi-xi-2)
N3,i(x)は、4つの2次式で構成されるが、区間xi-2=<x<xi-1に存在する2つの2次式は加算によって1つの2次式にまとまる。従って、N3,i(x)は、3つの2次式を連結したものとなる。x<xi-3,x=>xiの区間ではN3,i(x)=0になる。
この漸化式を用いると、関数N3,i(x)は、x=xi-2およびx=xi-1において関数値と一次微分係数が連続な曲線になることが確かめられる。
N4,i(x)など高次階のNr,i(x)も同様の漸化式で定義されるが、詳細は省略する。
N3,i(x)のxi-3をxi-2の方向に移動させ、xi-3=xi-2と重ねると、両節点は多重化される。こうすると、区間xi-1=<x<xiにある第3の2次式は変わらないが、区間xi-3=xi-2=<x<xi-1の第2の2次式は更新される。
更新された第2の2次式をy=ax^2+bx+cとすると、「x=xi-2のときy=0;x=xi-1のときyは正規化条件から決まる関数値;x=xi-1のときの一次微分係数が第3の2次式の同係数に一致」の3条件からa,b,cが求められる。これによってN3,i(x)は2つの2次式を連結したものに更新される。なお、第2の条件によって、x=xi-1のときの関数値は、第3の2次式の関数値に一致することが要請される。
同様に、N3,i(x)のxiをxi-1の方向に移動させ、節点xi-1=xiのように多重化したときも、区間xi-3=<x<xi-2の第1の2次式は変わらないが、区間xi-2=<x<xi-1=xiの第2の2次式は更新される。
同様に、N3,i(x)のxi-1,xi-2,xi-3をxi-1=xi-2=xi-3のように三重節点とすると、N3,i(x)の第3の2次式のみが更新されて残る。更新された第3の2次式をy=a(x-xi)^2とすると、x=xiのときy=0であるから、x=xi-1のときa(xi-1-xi)^2=1の正規化条件からaが求められる。N3,i(x)のxi,xi-1,xi-2を三重節点とする場合も同様の類推でy=a(x-xi-3)^2が決まる。
N3,i(x)に関し、x軸上の節点をx-2=x-1=x0=<x1<x2<...<xn=<xn+1=xn+2=xn+3とするとき、区間[x0,xn+1]において、2次のスプラインS(x)は2次のBスプラインの線形結合として表され、
S(x)=c1N3,1(x)+c2N3,2(x)+...+cn+3N3,n+3(x)
となる。nは多重節点以外にこの区間の内部に配置する節点の数である。ciは、Bスプライン係数である。
データ(Xj,Yj)(j=1,2,...,N)が与えられているとき、このデータをスプラインで補間する場合には、補間条件
S(Xj)=Yj
によってBスプライン係数ciを決定する。ここで、データの数(N)はパラメータの数n+3に一致させる必要がある。
Bスプラインの局所性により、区間[x0,xn+1]内の[x0,x1]など各小区間には3個のN3,i(x)のみが実際の計算に関与する。
例として、n=3とし、x0=0,x1=1,x2=2,x3=3,x4=4とする。X1=0,X2=0.5,X3=1.5,X4=2.5,X5=3.5,X6=4と設定すると、c1=Y1,c6=Y6が決定する。
残りのc2~c5を決定するためのS(Xj)に関する連立方程式は次の通りである。
c1N3,1(X2)+c3N3,3(X2)+c5N3,5(X2)=Y2
c2N3,2(X3)+c3N3,3(X3)+c5N3,5(X3)=Y3
c2N3,2(X4)+c4N3,4(X4)+c5N3,5(X4)=Y4
c2N3,2(X5)+c4N3,4(X5)+c6N3,6(X5)=Y5
ここで、N3,1(x)は(0,1);(1,0)を境界とする三重節点をもつBスプライン、N3,2(x)は(1,0);(4,0)を境界とする3連のBスプライン、N3,3(x)は(0,0);(2,0)を境界とする2連、N3,4(x)は(2,0);(4,0)を境界とする2連、N3,5(x)は(0,0);(3,0)を境界とする3連のBスプライン、N3,6(x)は(3,0);(4,0)を境界とする三重節点をもつBスプラインである。
例えば、小区間[1,2]において、N3,2(x)+N3,3(x)+N3,5(x)=1であることが確かめられる。すなわち、区間[0,4]においてN3,1(x)+...+N3,6(x)=1に正規化されていることを知る。
この方程式を解いてc2~c5が求められたら、各小区間について上式のXjの代わりにxの刻みを代入してyの値を計算する。
当然のことながら、S(x=Xj)=Yjとならなければならないから、この計算は、c2~c5の計算過程およびN3,1(x)~N3,6(x)の計算式のチェックにもなる。
下図は、Y1=2.1,Y2=2.3,Y3=1.9,Y4=1.7,Y5=2.4,Y6=2.6と設定し、Excelを用いてy=S(x)を計算し、グラフ表示したものである。

(X1,Y1)~(X6,Y6)をマーカー表示とし、スプライン補間した部分と区別した方が分かりやすくなるが、一部のデータ点(Xj,Yj)のみをマーカー表示する方法が見当たらないので、すべてのデータについてマーカー表示なしとした。
参考文献
吉本富士市著「インターネット時代の数学―スプライン」(共立出版)












※コメント投稿者のブログIDはブログ作成者のみに通知されます