流体力学の計算を楽しむ

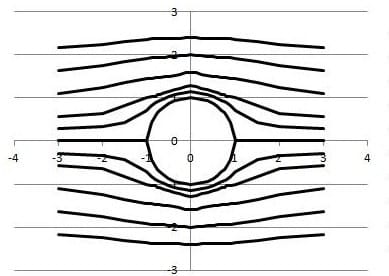
　流体力学を少しかじったのが縁で、一様流中に静止する円柱について、その流線を計算し、図示してみたくなった。流線とは、時間の経過とともに流れが変化しない定常流の場合には、流れのみちすじを示す曲線のことである。

　一般に流体について数学的モデルをつくるときの手順は、次のようなものであろう。まず流体の流線についてのデータを実験的に採取し、そのデータを表すような関数を求める。このとき、実変数の関数よりも、複素数を変数とする複素関数を求めるのがよいということになる。

　ここで、複素関数として、複素速度ポテンシャルという物理量を考えるのが正規の手順となっている。

　複素速度ポテンシャルｆは、ｉを虚数単位として、
　　　　　ｆ＝速度ポテンシャル＋ｉ×流れの関数
で与えられる。速度ポテンシャルは、流体に流速を生ぜしめるようなポテンシャル関数である。流れの関数は、流線を示す関数の集まりと考えられる。２次元の流れの場合、流れの関数（ｘ，ｙ）＝定数が流線を表す関数である。

　速度ポテンシャルと流れの関数とは、コーシー・リーマンの関係式で結ばれているので、流れの関数が求められれば、速度ポテンシャルを計算によって求めることができる。あるいは、複素関数ｆ（ｚ）をローラン展開したものの虚数部分が流れの関数を表現するように近似できれば、その実数部分はこの関係式を満たすことになる。

　以下の説明は、縮まない完全流体（粘性のない流体）の２次元の渦なし運動に関するものである。

　一様な流れについて、ｘ軸方向の速度をＵとすると、複素速度ポテンシャルは、ｚを複素変数として
　　　ｆ＝Ｕｚ，　Ｕ＞０
で与えられる。ｚ＝ｘ＋ｉｙであるから、
　　　速度ポテンシャル＝Ｕｘ
　　　流れの関数＝Ｕｙ
となる。

　次に、この一様流中の原点をその中心として静止する円柱を置いたときの複素速度ポテンシャルを考える。

　ここで、ｘ－ｙ平面上の点（ａ，０）に「わき出し」、点（－ａ，０）に「すいこみ」のある「二重わき出し」を考える。わき出した流体と同量の流体がすいこまれるとする。ａを無限に小さくとると、その複素速度ポテンシャルｆは、係数／ｚとなる。

　このような「二重わき出し」の流線は、ｙ＞０面内にあり原点に接する半径の異なる複数の円で構成される流線群と、ｙ＜０面にあり、この流線群と対称な流線群とより構成される。

　静止する円柱によってひきおこされる流れは、円柱の中心に「二重わき出し」をおいたときの流れと同等であるという。境界条件として、円柱の半径をａとし、一様流の速度をＵとすると、その複素速度ポテンシャルは、Ｕａ＾２／ｚとなる（＾はべき乗を表す）。

　速度ポテンシャルはラプラス方程式の解であるから、方程式は線形、流れの関数が解となるような方程式も線形であるから、上記２つの複素速度ポテンシャルは重ね合わせることができるので、結局、一様流中に静止する円柱に関する複素速度ポテンシャルは、
　　　ｆ＝Ｕｚ＋Ｕａ＾２／ｚ　　　　　（１）
となる。

　ここで、一様な流れは現実の流れに基づいているが、「二重わき出し」による流れは仮想的な流れであるから、両者を重ね合わせるということは、常識に反するような気がする。

　しかし、理論というものは、所詮は仮説であり、その結果がいかに現実をよく説明できるかだけが問題になるのだから、上記のような考えでよいのであろう。

　円柱から遠く離れると（Ｕａ＾２よりｚがはるかに大きくなると）、（１）式のｆはＵｚとなり、一様流を表す。

　簡単のためにａ＝１とする。ｚ＝ｘ＋ｉｙとおいて、ｆの虚数部分をとり出すと、
　　　流れの関数＝Ｕｙ－Ｕｙ／（ｘ＾２＋ｙ＾２）
が得られる。充分遠方の流線の１つは、ｙの一定値をｃとすると、Ｕｃとしてよいから、この流れと同一のみちすじとなる流線を表す関数は、
　　　ｙ－ｙ／（ｘ＾２＋ｙ＾２）＝ｃ
すなわち、
　　　ｙ＾３－ｃｙ＾２＋（ｘ＾２－１）ｙ＝ｃｘ＾２
で与えられる。

　そうすると、ｃ、すなわちｙの一定値を設定し、そのｃに関してｘのキザミを順次変えてｙについての３次方程式を解けばよい。これで１つの流線の軌跡が求められるから、ｃを変えて別の流線について３次方程式を作成し、同様の計算を繰り返せばよい。あるいは、ｘの一定値を設定し、そのｘに関してｃのキザミを順次変えてｙについての３次方程式をつくってもよい。

　この関数の形をみると、絶対値が同一のｘが正でも負でも同じ結果となるから、流線はｙ軸に関して対称となる。また、ｃ＞０，ｙ＞０とするこの関数の両辺に－１を掛けても成り立つから、ｃ＜０に変えると同一のｙが負に変わるだけであり、流線はｘ軸に関しても対称である。

　ｃ＝０に設定した流れのみちすじは、ｘ＜－１ではｘ軸上を流れ、ｘ＝－１で上下に分離し、ｘ＝１まで円柱の円周にまとわりつき、ｘ＞１からは再びｘ軸上を流れることがわかる。

　（１）式の実数部分は速度ポテンシャルであるから、これをｘで偏微分すると流速のｘ成分、ｙで偏微分すると流速のｙ成分が求められる。

　特に、円柱の表面の流速を求めるために、（１）式でｚ＝ａｅｘｐ（ｉｔ）とおくと（ｔはｘ軸からの偏角）、ｆは実数部分のみとなる。従って、速度ポテンシャルは、
　　　ｆ＝Ｕａｅｘｐ（ｉｔ）＋Ｕａｅｘｐ（－ｉｔ）＝２Ｕａｃｏｓｔ
により求められる。表面の流速は、
　　　ｖ（ｔ）＝（１／ａ）（ｆのｔに関する微分値）＝－２Ｕｓｉｎｔ
で求められる。－がつくのは、ｔの進む方向が流速の方向と逆になるためである。ｔ＝＋パイ／２（角度９０度）または－パイ／２では、一様流の速度Ｕの２倍になる。

　円柱表面での流体の圧力は、ベルヌーイの定理からおよその見当がつけられる。すなわち、流速が０のとき圧力は最大であり、流速の増加とともに圧力が減少していく。

　そうすると、円柱表面の各点にかかる圧力の大きさはｘ軸に関して対称、ｙ軸に関しても対称となる。圧力ベクトルの方向に関しても同様である。その結果、円柱表面全体が受ける圧力の総和は０である。言い換えれば、一様な流れに垂直におかれた円柱は、流体から力をうけないことになる。このことは、あきらかに日常の経験と反しているので、ダランベールの背理と呼ばれる。その原因は、流体が円柱表面と接するときに働く粘性力を無視したためである。

　Ｅｘｃｅｌのグラフ機能を使って、流線の計算結果をグラフ表示することにした。

　流線は、ｙ＞０領域に６本、ｙ＜０領域に６本、合計１２系列つくることにし、－３＜ｘ＜３を設定する列にｘのキザミ値を入力し、各系列に計算結果のデータを入力した。円柱に沿った流線のデータを入力するために、ＥｘｃｅｌのＳＱＲＴ関数を利用した。



　参考文献
　今井功著「物理テキストシリーズ　流体力学」（岩波書店）
　金丸隆志著「理系のためのＥｘｃｅｌグラフ入門」（ブルーバックス）