三次元空間内で共有点をもたない単純閉折線と呼ばれる多辺形を「結び目」という。この結び目をz軸と平行に二次元平面上に射影すると、一般に多重点をもつ閉折線が得られる。空間上の単純閉折線の辺の位置を移動することによって、二次元平面上の閉折線が有限個の2重点のみをもつようにできる。平面上の2重点、すなわち交差点は、空間上でz座標の大きい方の上交差点と、小さい方の下交差点とが重なった点である。
結び目の射影像の各2重点について、下交差点を含む辺に対応する辺に図のように切れ目を入れて空間的な感じを出すように表示する。なお、位相幾何学では直線と曲線の区別はないので、閉折線を閉曲線に代えて表示している。
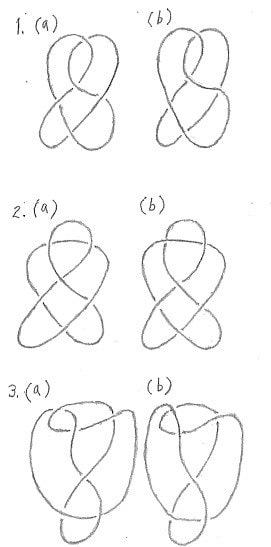
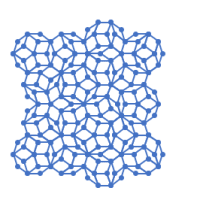
図の1に示す結び目は5個の交差点をもち、2に示す結び目は6個の交差点をもつ。結び目には、交差点のいくつかを解消できるタイプと、解消できないタイプとがある。交差点を解消できずに残る交差点の個数を最小交差数という。最小交差数は、結び目の型を決める最も単純な不変量となる。一方、交差点が解消されてその個数がゼロになった結び目は、単純閉曲線、すなわち円であり、平凡型と呼ばれる。
図1(a)(b)の一方は最小交差数をもつ結び目、他方は平凡型である。図2(a)(b)および図3(a)(b)についても同様である。ここで(a)(b)のうち、どちらが平凡型かを当てるのが演習問題である。
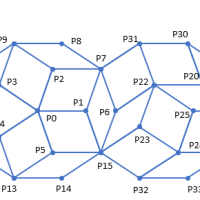
図1(b)は、下図に示すように、領域Aの外周線が上交差線なので、下交差線より内側に引き込むと領域Bと合併するとともに、交差点が2つ消える。領域ABの外周線は、もう一つの下交差線の外に移動できてさらに交差点が2つ消えて交差点はただ1つだけとなる。この形の結び目は、交差点なしと同値なので、結局、平凡型であることが分かる。図1(a)は、どの交差点も解消できないので、最小交差数5の結び目型である。
図2(a)は、領域Aの外周線を移動することによって交差点を2つ消すことができる。領域Bの外周線も同様の移動によって、さらに交差点2つを消せる。領域Aと領域Bは合併できて、交差点が1つ消え、領域ABとなる。これは交差点なしの結び目と同値なので、結局、平凡型となる。図2(b)は、最小交差数6の結び目型である。
図3(b)の領域AとBは合併によって交差点が2つ消え、同値関係からさらに交差点が1つ消える。領域CとDは合併によって交差点が2つ消え、残った1つの交差点も同値関係から消えて、結局、平凡型となる。図3(a)は、最小交差数6の結び目型である。
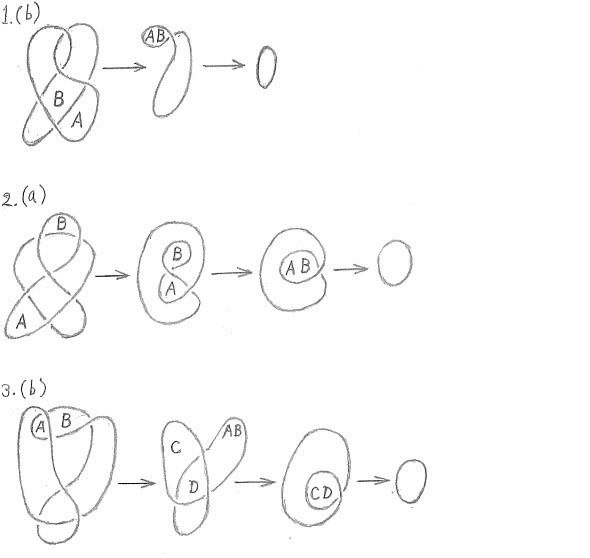
参考文献
鈴木普一著「結び目理論入門」(サイエンス社)
結び目の射影像の各2重点について、下交差点を含む辺に対応する辺に図のように切れ目を入れて空間的な感じを出すように表示する。なお、位相幾何学では直線と曲線の区別はないので、閉折線を閉曲線に代えて表示している。

図の1に示す結び目は5個の交差点をもち、2に示す結び目は6個の交差点をもつ。結び目には、交差点のいくつかを解消できるタイプと、解消できないタイプとがある。交差点を解消できずに残る交差点の個数を最小交差数という。最小交差数は、結び目の型を決める最も単純な不変量となる。一方、交差点が解消されてその個数がゼロになった結び目は、単純閉曲線、すなわち円であり、平凡型と呼ばれる。
図1(a)(b)の一方は最小交差数をもつ結び目、他方は平凡型である。図2(a)(b)および図3(a)(b)についても同様である。ここで(a)(b)のうち、どちらが平凡型かを当てるのが演習問題である。
図1(b)は、下図に示すように、領域Aの外周線が上交差線なので、下交差線より内側に引き込むと領域Bと合併するとともに、交差点が2つ消える。領域ABの外周線は、もう一つの下交差線の外に移動できてさらに交差点が2つ消えて交差点はただ1つだけとなる。この形の結び目は、交差点なしと同値なので、結局、平凡型であることが分かる。図1(a)は、どの交差点も解消できないので、最小交差数5の結び目型である。
図2(a)は、領域Aの外周線を移動することによって交差点を2つ消すことができる。領域Bの外周線も同様の移動によって、さらに交差点2つを消せる。領域Aと領域Bは合併できて、交差点が1つ消え、領域ABとなる。これは交差点なしの結び目と同値なので、結局、平凡型となる。図2(b)は、最小交差数6の結び目型である。
図3(b)の領域AとBは合併によって交差点が2つ消え、同値関係からさらに交差点が1つ消える。領域CとDは合併によって交差点が2つ消え、残った1つの交差点も同値関係から消えて、結局、平凡型となる。図3(a)は、最小交差数6の結び目型である。
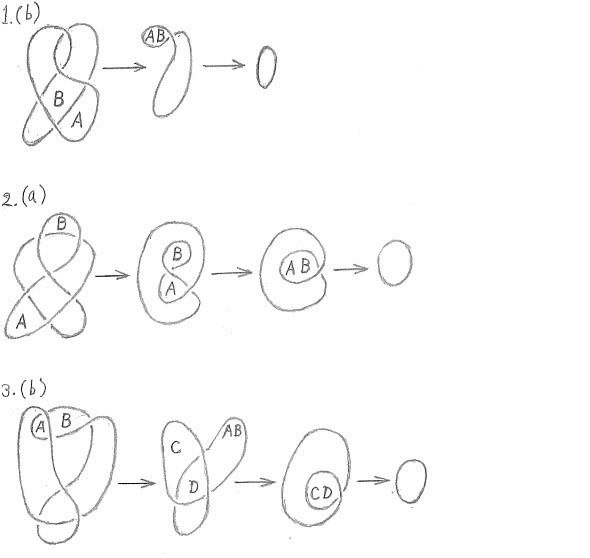
参考文献
鈴木普一著「結び目理論入門」(サイエンス社)












※コメント投稿者のブログIDはブログ作成者のみに通知されます