3次元球面S3とは、方程式
x^2+y^2+z^2+w^2=1
で表される図形である。この方程式を満足する解は4次元空間上の点(x,y,z,w)であるため、S3の図形を描くには目には見えない4次元空間を考える必要がある。
2次元球面S2であれば、地球の表面のように目に見える図形であるので、その形態を想像するのは容易である。S2上に、北極点pと赤道に相当する大円を設定することができる。赤道とは、1次元球面(円)S1であり、赤道面とも言える2次元球体(円板)B2のヘリとなる円のことである。S2上の各点と点pとを結ぶ直線は、点p自身を除いて(x,y)平面上にその点の像を射影する。よって赤道もこの平面上に拡大された円として射影される。そうすると、S2の南半球の各点は射影された赤道円の内部に、北半球の点はその外部に射影されることになる。
3次元球面S3の赤道は、2次元球面S2であり、赤道面に相当するものは3次元球体(球の中身)B3である。赤道は、このB3のヘリとなる。S3は赤道面の写像であり、赤道を境界として北半球部分と南半球部分とに分かれる。S3上の各点とS3の北極点pとを結ぶ直線は、点p自身を除いて(x,y,z)空間上にその点の像を射影する。
S3の赤道は、円ではなく、赤道軸に沿って球面S2が一周したものであるため、その形状を想像するのが難しい。また、S3の各点は、3次元空間(x,y,z)内に射影されるため、赤道部分の射影像を境界として、南半球部分の各点と北半球部分の各点の射影像がどのように分布するのか、その図形の構造を想像できそうもない。
ここで、複素数を用いて3次元球面S3を表現することにする。z1,z2を次のような複素数
z1=x+iy; z2=z+iw
とする。そうすると、
ABS(z1)^2=x^2+y^2; ABS(z2)^2=z^2+w^2
と表現できる。
3次元球面S3を構成する4次元空間の点(x,y,z,w)は、複素数の組(z1,z2)の全体がつくる集合と1対1に対応するので、S3を複素数z1,z2を変数とする疑似的な2次元平面において、
S3={(z1,z2)|ABS(z1)^2+ABS(z2)^2=1}
と表せる。
つまり、(z1,z2)平面において複素数の組(z1,z2)の全体は半径1の円をつくる。この円は、S3の大円であり、無数の大円を含むが、特に
ABS(z1)^2=1/2かつABS(z2)^2=1/2
の条件を満足する点(x,y,z,w)の集合を、赤道部分が1つの円に縮約されたものとみなしてよい。
ABS(z1)^2=1/2は、点(x,y)の集合が半径SQR(1/2)の円をつくり、ABS(z2)^2=1/2は、点(z,w)の集合が同じ半径の円をつくる。赤道部分は、両者を併せたもので構成されているのである。つまり、赤道部分は、実は半径SQR(1/2)の円の切り口をもつトーラス(ドーナツの表面)の形状をしていることがわかる。
4次元空間にある赤道部分を3次元空間に射影すると、トポロジカルな構造は保存されるが、そのサイズは変更される。
S3を次の2つの部分に分割する。
V1: (z1,z2)はS3に含まれ、ABS(z1)^2=<1/2
V2: (z1,z2)はS3に含まれ、ABS(z2)^2=<1/2
このとき、S3はV1とV2から構成され、北極p(0,0,0,1)はV1に含まれる。V1とV2の共通部分V0は、上記の条件を満たす赤道部分である。
S3から北極pを取りさると、S3のすべての点は3次元空間内に射影された図形として見ることができる。S3の赤道部分(V0)はトーラスの形状が射影され、V2はトーラスとその中身(中身の詰まったトーラス)に対応し、その外部が点pを除いたV1に対応する。
上記V1とV2の定義からわかるように、V1とV2は、z1とz2を入れ替えただけなので、V1が中身の詰まったトーラスであってもよい。いずれにしても、V1とV2は、それぞれ共通の境界であるトーラスV0と接している。
3次元球面S3の図形を表現するために複素数を用いることによって、S3のトポロジカルな構造が明確になる。
参考文献
西川青季著「見えないものを見えるようにして考える幾何学」(数学セミナー2022.04)
x^2+y^2+z^2+w^2=1
で表される図形である。この方程式を満足する解は4次元空間上の点(x,y,z,w)であるため、S3の図形を描くには目には見えない4次元空間を考える必要がある。
2次元球面S2であれば、地球の表面のように目に見える図形であるので、その形態を想像するのは容易である。S2上に、北極点pと赤道に相当する大円を設定することができる。赤道とは、1次元球面(円)S1であり、赤道面とも言える2次元球体(円板)B2のヘリとなる円のことである。S2上の各点と点pとを結ぶ直線は、点p自身を除いて(x,y)平面上にその点の像を射影する。よって赤道もこの平面上に拡大された円として射影される。そうすると、S2の南半球の各点は射影された赤道円の内部に、北半球の点はその外部に射影されることになる。
3次元球面S3の赤道は、2次元球面S2であり、赤道面に相当するものは3次元球体(球の中身)B3である。赤道は、このB3のヘリとなる。S3は赤道面の写像であり、赤道を境界として北半球部分と南半球部分とに分かれる。S3上の各点とS3の北極点pとを結ぶ直線は、点p自身を除いて(x,y,z)空間上にその点の像を射影する。
S3の赤道は、円ではなく、赤道軸に沿って球面S2が一周したものであるため、その形状を想像するのが難しい。また、S3の各点は、3次元空間(x,y,z)内に射影されるため、赤道部分の射影像を境界として、南半球部分の各点と北半球部分の各点の射影像がどのように分布するのか、その図形の構造を想像できそうもない。
ここで、複素数を用いて3次元球面S3を表現することにする。z1,z2を次のような複素数
z1=x+iy; z2=z+iw
とする。そうすると、
ABS(z1)^2=x^2+y^2; ABS(z2)^2=z^2+w^2
と表現できる。
3次元球面S3を構成する4次元空間の点(x,y,z,w)は、複素数の組(z1,z2)の全体がつくる集合と1対1に対応するので、S3を複素数z1,z2を変数とする疑似的な2次元平面において、
S3={(z1,z2)|ABS(z1)^2+ABS(z2)^2=1}
と表せる。
つまり、(z1,z2)平面において複素数の組(z1,z2)の全体は半径1の円をつくる。この円は、S3の大円であり、無数の大円を含むが、特に
ABS(z1)^2=1/2かつABS(z2)^2=1/2
の条件を満足する点(x,y,z,w)の集合を、赤道部分が1つの円に縮約されたものとみなしてよい。
ABS(z1)^2=1/2は、点(x,y)の集合が半径SQR(1/2)の円をつくり、ABS(z2)^2=1/2は、点(z,w)の集合が同じ半径の円をつくる。赤道部分は、両者を併せたもので構成されているのである。つまり、赤道部分は、実は半径SQR(1/2)の円の切り口をもつトーラス(ドーナツの表面)の形状をしていることがわかる。
4次元空間にある赤道部分を3次元空間に射影すると、トポロジカルな構造は保存されるが、そのサイズは変更される。
S3を次の2つの部分に分割する。
V1: (z1,z2)はS3に含まれ、ABS(z1)^2=<1/2
V2: (z1,z2)はS3に含まれ、ABS(z2)^2=<1/2
このとき、S3はV1とV2から構成され、北極p(0,0,0,1)はV1に含まれる。V1とV2の共通部分V0は、上記の条件を満たす赤道部分である。
S3から北極pを取りさると、S3のすべての点は3次元空間内に射影された図形として見ることができる。S3の赤道部分(V0)はトーラスの形状が射影され、V2はトーラスとその中身(中身の詰まったトーラス)に対応し、その外部が点pを除いたV1に対応する。
上記V1とV2の定義からわかるように、V1とV2は、z1とz2を入れ替えただけなので、V1が中身の詰まったトーラスであってもよい。いずれにしても、V1とV2は、それぞれ共通の境界であるトーラスV0と接している。
3次元球面S3の図形を表現するために複素数を用いることによって、S3のトポロジカルな構造が明確になる。
参考文献
西川青季著「見えないものを見えるようにして考える幾何学」(数学セミナー2022.04)










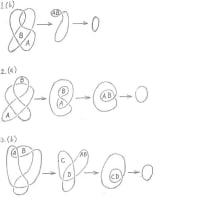


※コメント投稿者のブログIDはブログ作成者のみに通知されます