写経 11.「積分」（その4） 『好きになる数学入門 第6巻』 宇沢弘文

「東京帝大におけるアインシュタイン教授特別講演（1922年〔大正11年〕11月）　聴講者　　　『アインシュタインの東京大学講義録』杉本賢治　編著

京都帝大理学博士　西内貞吉
横濱商工教授　　　池内本
　〃　　　　　　　中西勝治
東京帝大工科講師　谷　安正
東京帝大理学博士　竹内端三
東京高工教授　　　竹内時男
第一高等学校教授　竹内潔
東京帝大理学博士　寺田寅彦　　　　　


　と、寺田寅彦の名前も見える。以下、学生まで含めて、聴講者135名。ただ、名簿の配列が、微妙にアイウエオ順のような、そうでないような奇妙な感じ（笑）。まんなか位に、東京帝大理科学長　長岡半太郎の名前がある。
　ここでこの本を紹介したのは、同じく講義を聴講した荒木俊馬（砲工学校教授）の残した講義録に、「アインシュタインは∫を下から書いた」　と載っていたからである。





　“広田先生が、こんな事を云う。「どうも物理学者は自然派じゃ駄目の様だね」
　物理学者と自然派の二字は少なからず満場の興味を刺激した。
　「それはどう云う意味ですか」と本人の野々宮さんが聞き出した。広田先生は説明しなければならなくなった。”　『三四郎』夏目漱石　1908年（明治41年）9～12月、「朝日新聞」に連載。













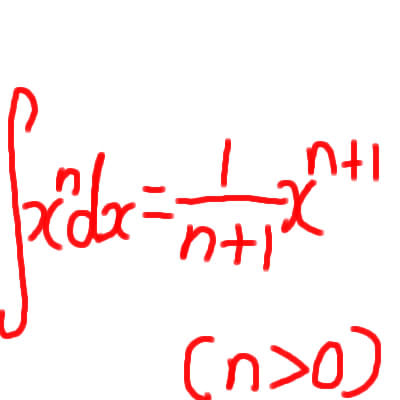
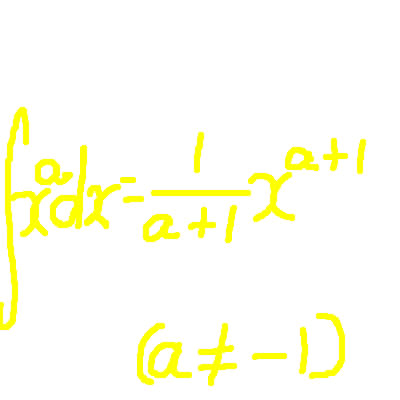
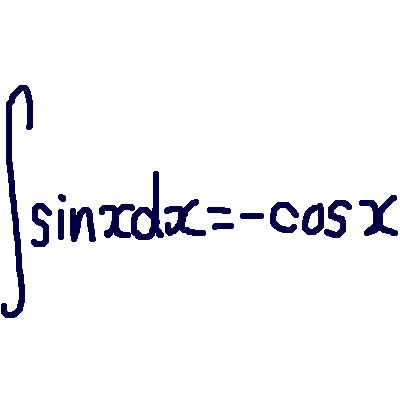
「第2章　積分の計算　（扉）」宇沢弘文

写経 10.「積分」（その3） 『好きになる数学入門 第6巻』 宇沢弘文

　“語学を修得するに〔は〕まず単語を覚え文法を覚えなければならない。しかしただそれを一通り理解し暗記しただけでは自分で話す事も出来なければ文章も書けない。永い修練によってそれをすっかり体得した上で、始めて自分自身の考えを運ぶ道具にする事が出来る。
　数学でも、ただ教科書や講義のノートにある事柄を全部理解しただけではなかなか自分の用には立たない。やはり色々な符号の意味をすっかり徹底的にのみ込む事は勿論、また色々な公式をかなりの程度まで暗記して、一度わがものにしてしまわなければ実際の計算は困難である。”　寺田寅彦







　「第２章　積分の計算」


　第１章の第３節では,任意に与えられた関数ｆ（ｘ）の不定積分Ｆ（ｘ)は変数ｘで微分するともとの関数ｆ（ｘ）にもどるという性質によって特徴づけられることを証明しました.不定積分



　　　　　　　　　　　　　　Ｆ（ｘ）＝∫ｆ（ｘ）ｄｘ


をｘについて微分すると,




　　　　　　　　　　　　　　Ｆ’（ｘ）＝ｆ（ｘ）



　この性質を使って,まずいくつかのかんたんな関数の不定積分を計算し,だんだんとむずかしい関数の不定積分を扱っていくことにします.（不定積分をたんに積分ということもあります・）


　宇沢弘文

写経 9.「積分」（その2） 『岩波数学入門辞典』

　“数学では最初に若干の公理前提を置いて、あとは論理に従って前提の中に含まれているものを分析し、分析したものを組み立ててゆくのであるが、我々の言語に依って考えを運んでゆく過程もかなりこれと似た所がある。勿論、数学の公理や論理は極めて簡単明瞭であり、使用される概念も明確に制定されているに反して、言語による思考の場合では、これらすべてのものが複雑に多義的であるから、一見同様な前提から多種多様な結論が生れ出るように見える。しかし実際の場合に前提の数が非常に多いから全く同一な前提群から出発するという事は実はあり得ないのである。”　寺田寅彦　（寺田の引用は全集から）








　「積分」　integral　　　

　
　積分と称されるものは数多いが,2種類に大別される.
　第1は微分の逆演算を定める積分で,不定積分がこれに当る.例えば時刻０からｔ　までに動点が進む道のりＦ（ｔ）を,動転の速度ｆ（ｔ）から求めることは,Ｆ（ｔ)の微分がｆ（ｔ）であるから,微分の逆演算である.微分方程式を解くことを「積分する」というのもこの見方の例である.

　第2の積分は,微小な量の「無限個の和」を求める操作であり,定積分と呼ばれる.例えば,2次元の図形を無限個の線分の集まりとみなして面積を求めることが,それに当る.正値関数のグラフ
ｙ＝ｆ（ｘ）と直線ｘ＝ａ,　ｘ＝ｂ,　ｙ＝０　で囲まれた図形の場合,線分｛（ｘ,ｙ）｜ｘ＝ｔ,０≦ｙ≦ｆ（ｔ）｝の長さがｆ（ｔ）であるから,その面積は積分




　　　　　　　　　　　　　　　　　　　　　　　　　　　　




である.歴史的には,ギリシア時代のアルキメデスによる球面積の公式の導出などにこの考え方は現れている.ちなみに,積分の記号∫は和（sum）を表す ｓ を縦に長くのばした形である.
　
　これら2種類の積分が同じものであるということが,微分積分学の基本定理であり,その発見によって,面積などを組織的に計算する方法が確立し,微分積分学が成立した.定積分は,リーマン積分として厳密な形で定式化される.また,微分積分学の基本定理は,その多次元版である微分形式の積分とストークスの定理に一般化される.

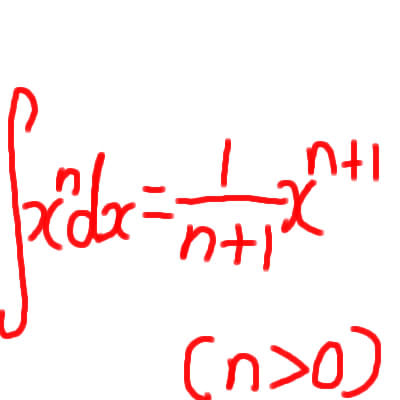
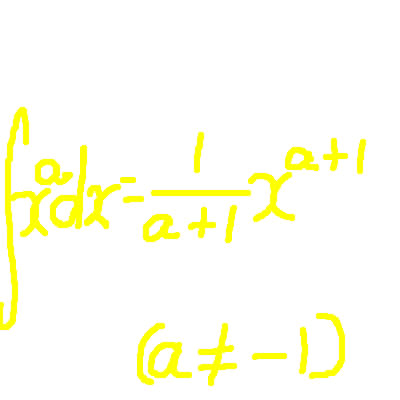
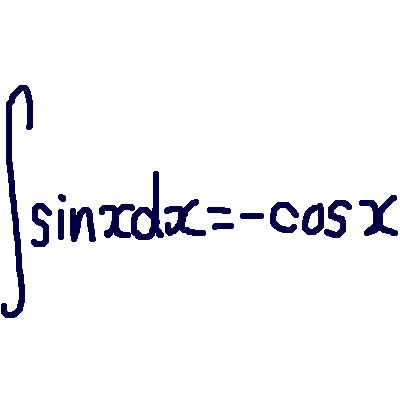
　物の「密度」（微小な部分にある物の量）が各点で定まっているとき,その総和を求めることも積分である.これは密度積分と呼ばれる.関数ｆ（ｘ）の重み付き積分∫ｆ（ｘ）ｗ（ｘ）ｄｘ　やスティルチェス積分∫ｆ（ｘ）ｄＦ（ｘ）はその例である.この見方は,測度および測度に関する積分に発展した（ルベーグ積分）.ここからは,測度に関する微分（ラドン-ニコディム微分という）の概念なども誕生しており,微分積分学は別の方向へ拡張される.