図のように、円の内側に一辺の長さが円の半径に等しい正方形ABCDがある。この正方形ABCDが円の内側に沿って矢印の方向に滑ることなく回転しながら移動するとき、頂点Aの描く軌跡として最も妥当なのはどれか。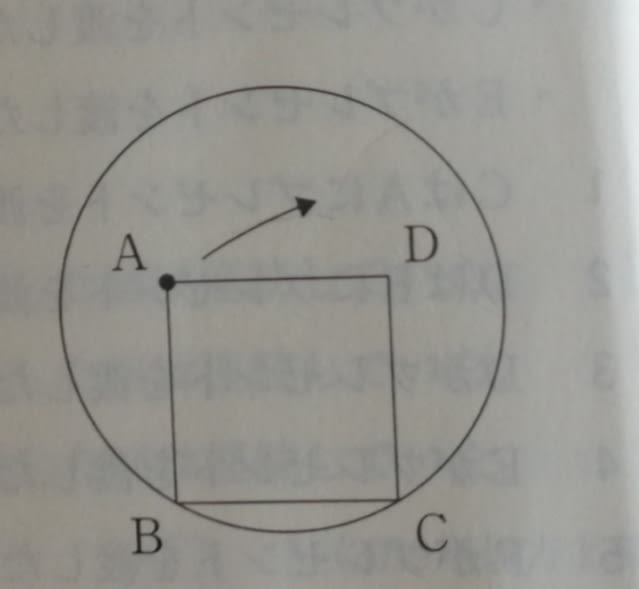

結論から言うと、「ピョン、ピョン、ピョンで3分の1(3分の2でもOK)だから正解は肢2」なのです。 図を一つ左に転がすと、点Aは円周上にきます。そこから、右に3回転がると、点Aは再び円周上にきます。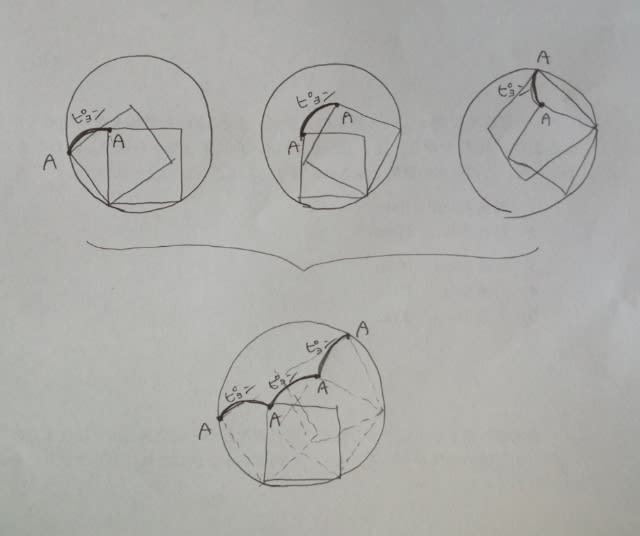
そして、はじめのAから、最後のAまでの距離は、円周上では約3分の1(実際ピッタリ3分の1)。逆回りで見ると3分の2。
そのような選択肢は2しかありません。
ここをポチッとお願いします。→


結論から言うと、「ピョン、ピョン、ピョンで3分の1(3分の2でもOK)だから正解は肢2」なのです。 図を一つ左に転がすと、点Aは円周上にきます。そこから、右に3回転がると、点Aは再び円周上にきます。

そして、はじめのAから、最後のAまでの距離は、円周上では約3分の1(実際ピッタリ3分の1)。逆回りで見ると3分の2。

そのような選択肢は2しかありません。
ここをポチッとお願いします。→
にほんブログ村













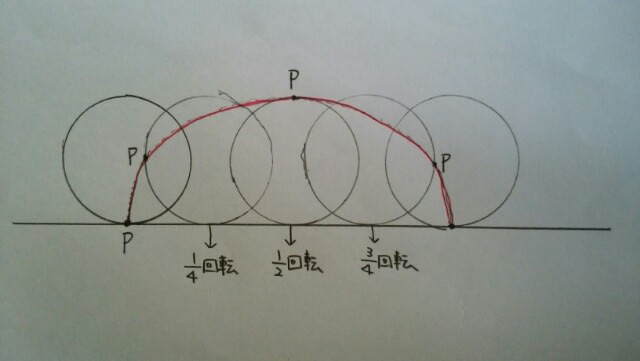
 サイクロイド曲線や、円周上の点の軌跡について不明な人は、1つ前の記事を参考にして下さいね。小さい円の円周は、2πだから、
サイクロイド曲線や、円周上の点の軌跡について不明な人は、1つ前の記事を参考にして下さいね。小さい円の円周は、2πだから、 ゆえに、P1からP2までは、サイクロイド曲線。(緑色)
ゆえに、P1からP2までは、サイクロイド曲線。(緑色) P3からP4も同じ。
P3からP4も同じ。 組み合わせて、(緑色)
組み合わせて、(緑色) 次に、P2からP3。(赤色)
次に、P2からP3。(赤色) 右側も左側も同じですから、
右側も左側も同じですから、 となり、正解は肢②です。
となり、正解は肢②です。

 この曲線は、扇形とは違う形です。もしも、円の半径が1だったら、
この曲線は、扇形とは違う形です。もしも、円の半径が1だったら、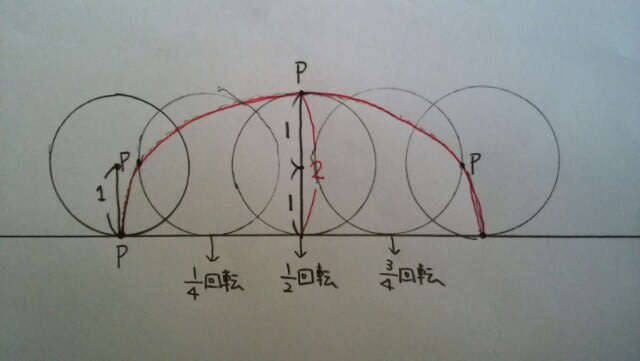 ですね。では、その次。半径が1の円が、半径が2の円の内側を回転すると、円周上の点は、半径が2の円の直径上を動きます。えっ?何を言ってるのか分からない?とにかく、次の図を見て、覚えて下さい。
ですね。では、その次。半径が1の円が、半径が2の円の内側を回転すると、円周上の点は、半径が2の円の直径上を動きます。えっ?何を言ってるのか分からない?とにかく、次の図を見て、覚えて下さい。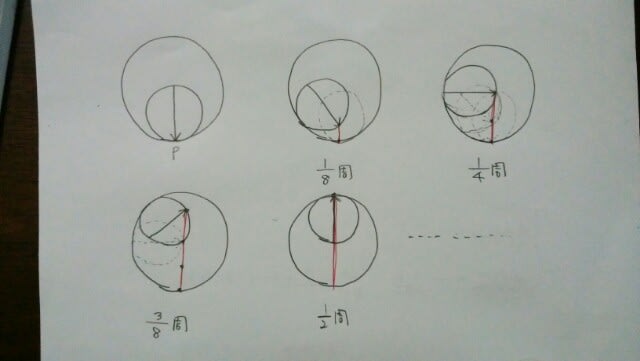
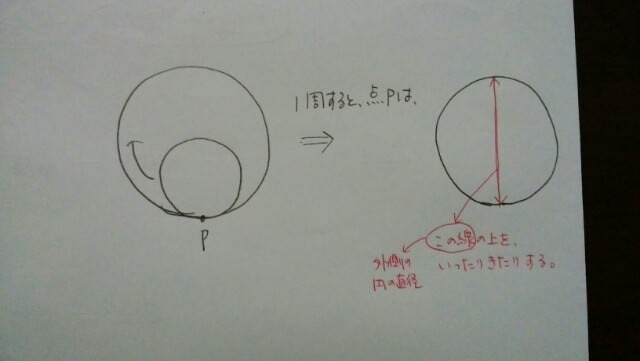 それ以外にも、覚えておくことがあります。①円が円の外側を転がるとき。
それ以外にも、覚えておくことがあります。①円が円の外側を転がるとき。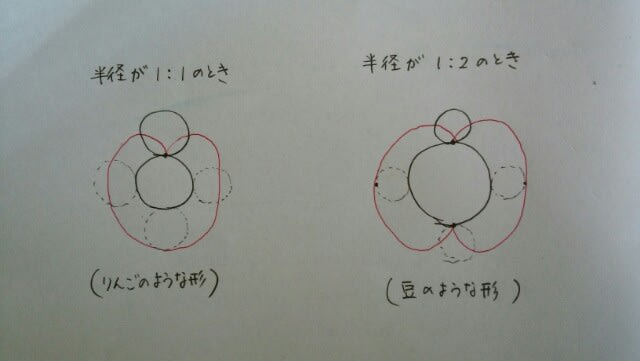
 ②円が円の外側を転がるとき。
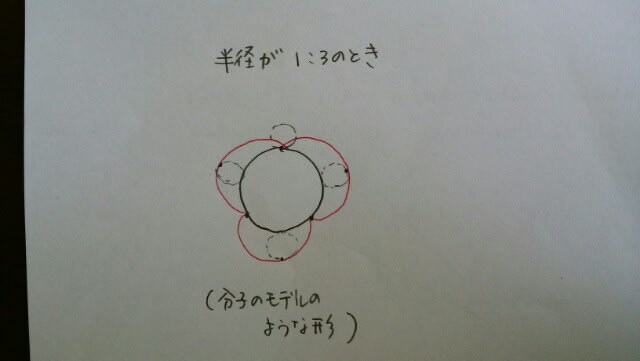
②円が円の外側を転がるとき。 半径が1:3のときは、円周を3等分する点をとって、少し内側にくびれた曲線になっています。だから、半径が1:4であれば、円周を4等分する点をとって、少し内側にくびれた曲線を描けばOK。何対何でも同じようにすればよいのです。次回、東京消防庁1類の問題を紹介します。
半径が1:3のときは、円周を3等分する点をとって、少し内側にくびれた曲線になっています。だから、半径が1:4であれば、円周を4等分する点をとって、少し内側にくびれた曲線を描けばOK。何対何でも同じようにすればよいのです。次回、東京消防庁1類の問題を紹介します。
 必要な知識は、次の3つです。
必要な知識は、次の3つです。
 本問は、半径が1:4なので、
本問は、半径が1:4なので、 そして、半円Bに沿って回転するので、
そして、半円Bに沿って回転するので、 正解は肢⑤です。
正解は肢⑤です。
 ①ア②イ③ウ④エ⑤オ 円が転がるときの、円の中心の軌跡と、円周上の点の軌跡は、次のようになります。
①ア②イ③ウ④エ⑤オ 円が転がるときの、円の中心の軌跡と、円周上の点の軌跡は、次のようになります。 扇形の場合は、次のようになります。
扇形の場合は、次のようになります。
 ポイントは、ここです。
ポイントは、ここです。 そうすると、本問では、
そうすると、本問では、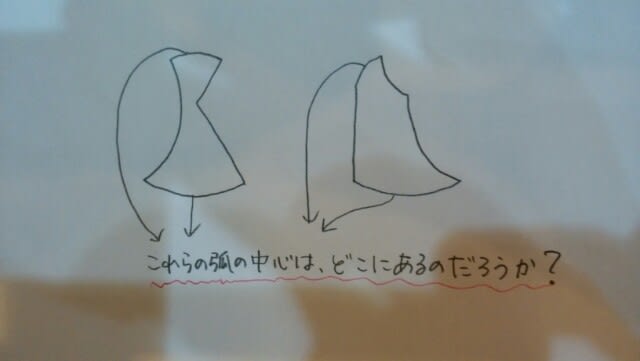 ということになりますね。
ということになりますね。 次に、
次に、 同じ記号どうしは、同じ軌跡になっています。○、△、×、□、☆で、元に戻っています。その間に、横一直線が2回出てきますね。(×と☆)そして、地面にくっつくときがあります。点アは、図形の内側にある点だから、地面にくっつくことはありません。
同じ記号どうしは、同じ軌跡になっています。○、△、×、□、☆で、元に戻っています。その間に、横一直線が2回出てきますね。(×と☆)そして、地面にくっつくときがあります。点アは、図形の内側にある点だから、地面にくっつくことはありません。 結局、○地面にくっつかない。○横一直線の軌跡が二つある。以上二つの理由で、正解は肢3です。要するに、図形Aと図形Bは、このような形に変形して考えれば速かったのです。
結局、○地面にくっつかない。○横一直線の軌跡が二つある。以上二つの理由で、正解は肢3です。要するに、図形Aと図形Bは、このような形に変形して考えれば速かったのです。
