問題再掲。三つの正の整数a、b、cが次の条件を満たすとき、a+b+cはいくらか。 ・a<b<c<10である。 ・aは奇数である。 ・bとcの差は3である。 ・aとcの平均は、bより小さい整数である。 3番目と4番目の条件をどうとらえるかで、解き方が微妙に違ってきますが、もちろん正解は一つです。数直線で考えると、 となりますが、4番目の条件を図に書き込むことが難しくなります。 でも、たかが10までの整数(厳密には9まで)の話なので、なんとなればすべて書き出して調べまくれば、何とでもなるだろう!と、お気楽派。やってみましょう。bとcは差が3なので、
となりますが、4番目の条件を図に書き込むことが難しくなります。 でも、たかが10までの整数(厳密には9まで)の話なので、なんとなればすべて書き出して調べまくれば、何とでもなるだろう!と、お気楽派。やってみましょう。bとcは差が3なので、 ところで、4番目の条件より、もしもcが偶数だったら、a+cが奇数になってしまい、aとcの平均は、整数になりません。よって、cは奇数。
ところで、4番目の条件より、もしもcが偶数だったら、a+cが奇数になってしまい、aとcの平均は、整数になりません。よって、cは奇数。 aとcの平均はbより小さいという条件から、
aとcの平均はbより小さいという条件から、 これを満たすものは一つだけです。
これを満たすものは一つだけです。 以上より、a=1、b=6、c=9。a+b+c=1+6+9=16。正解は16でした。数直線ではなく、方程式や不等式で考えると、
以上より、a=1、b=6、c=9。a+b+c=1+6+9=16。正解は16でした。数直線ではなく、方程式や不等式で考えると、 ②式より、b=c-3。これを③式に代入して、
②式より、b=c-3。これを③式に代入して、 なので、いきなり、c=9、b=6、a=1です。
なので、いきなり、c=9、b=6、a=1です。 ここをポチッとお願いします。→
ここをポチッとお願いします。→
にほんブログ村

 となりますが、4番目の条件を図に書き込むことが難しくなります。 でも、たかが10までの整数(厳密には9まで)の話なので、なんとなればすべて書き出して調べまくれば、何とでもなるだろう!と、お気楽派。やってみましょう。bとcは差が3なので、
となりますが、4番目の条件を図に書き込むことが難しくなります。 でも、たかが10までの整数(厳密には9まで)の話なので、なんとなればすべて書き出して調べまくれば、何とでもなるだろう!と、お気楽派。やってみましょう。bとcは差が3なので、 ところで、4番目の条件より、もしもcが偶数だったら、a+cが奇数になってしまい、aとcの平均は、整数になりません。よって、cは奇数。
ところで、4番目の条件より、もしもcが偶数だったら、a+cが奇数になってしまい、aとcの平均は、整数になりません。よって、cは奇数。 aとcの平均はbより小さいという条件から、
aとcの平均はbより小さいという条件から、 これを満たすものは一つだけです。
これを満たすものは一つだけです。 以上より、a=1、b=6、c=9。a+b+c=1+6+9=16。正解は16でした。数直線ではなく、方程式や不等式で考えると、
以上より、a=1、b=6、c=9。a+b+c=1+6+9=16。正解は16でした。数直線ではなく、方程式や不等式で考えると、 ②式より、b=c-3。これを③式に代入して、
②式より、b=c-3。これを③式に代入して、 なので、いきなり、c=9、b=6、a=1です。
なので、いきなり、c=9、b=6、a=1です。 ここをポチッとお願いします。→
ここをポチッとお願いします。→にほんブログ村













 前回と同じタイプの問題です。五角形のまわりに四角形が二つと三角形が三つありますね。なので、
前回と同じタイプの問題です。五角形のまわりに四角形が二つと三角形が三つありますね。なので、 前回と同じで、対頂角は等しいので、対頂角どうしは同じ記号にしてあります。図より、a+b+c+d+e+f+g+2h+2i+2j+2k+2l=360+360+180+180+180=1260º。ところで、何角形でも、外角の和は360ºです。(重要定理)ゆえに、
前回と同じで、対頂角は等しいので、対頂角どうしは同じ記号にしてあります。図より、a+b+c+d+e+f+g+2h+2i+2j+2k+2l=360+360+180+180+180=1260º。ところで、何角形でも、外角の和は360ºです。(重要定理)ゆえに、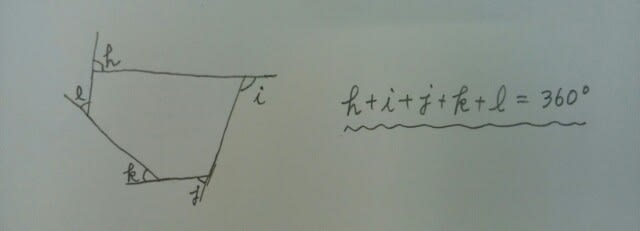 なので、2h+2i+2j+2k+2l=720ºです。さあ、必要なくなったら、ポイッ(-_- )ノ⌒。
なので、2h+2i+2j+2k+2l=720ºです。さあ、必要なくなったら、ポイッ(-_- )ノ⌒。 正解は、540ºでした。ここをポチッとお願いします。→
正解は、540ºでした。ここをポチッとお願いします。→
 正解は、明日午前中。分かった人はポチしてね。分からなかったときもポチしてね。→
正解は、明日午前中。分かった人はポチしてね。分からなかったときもポチしてね。→
 三角形の内角の和は180º、四角形は360º、五角形は540ºです。なので、
三角形の内角の和は180º、四角形は360º、五角形は540ºです。なので、 角j、k、lは求める角の和には入っていないのですが、まあ、とりあえず仲間に入れてあげます。そうしないと、180º、360º、540ºにならないからです。 ①+②+③より、a+b+c+d+e+f+g+h+i+j+k+l=180+360+540=1080ºです。ところで、対頂角は等しいので、j+k+l=180º。
角j、k、lは求める角の和には入っていないのですが、まあ、とりあえず仲間に入れてあげます。そうしないと、180º、360º、540ºにならないからです。 ①+②+③より、a+b+c+d+e+f+g+h+i+j+k+l=180+360+540=1080ºです。ところで、対頂角は等しいので、j+k+l=180º。 j、k、lはもう必要ありませんので、ポイッ(-_- )ノ⌒。
j、k、lはもう必要ありませんので、ポイッ(-_- )ノ⌒。 正解は、900ºでした。ここをポチッとお願いします。→
正解は、900ºでした。ここをポチッとお願いします。→ 昨日は、久しぶりに四条大橋を渡りました。あの大雨のとき以来です。鴨川、元に戻ってました。
昨日は、久しぶりに四条大橋を渡りました。あの大雨のとき以来です。鴨川、元に戻ってました。
 河原町通り、交通規制でがら~ん…
河原町通り、交通規制でがら~ん…