地方上級の判断推理 5

2021年出題。　　　　　　　　　　　　　　　　　　　　　　6つの作業A〜Fからなるプロジェクトがあり、それぞれの作業について、一日の作業人数、作業日程、先行作業（開始までに終わらせていなければいけない作業）が次の表のとおりである。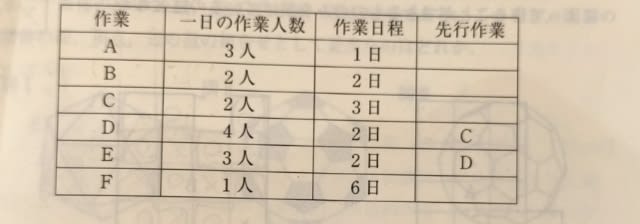
プロジェクトは連続する7日間で行い、一日の作業人数が最大5人になるように日程を組んだ。　　　　　　　　　　　　　　　　　　　　　このとき正しく言えることは次のうちどれか。　　　　　　　　　　　　　　　　　　　　　　　　なお、各作業日程は連続して行うものとする。　　　　　　　　　　　　　　　　　　　　　　①作業Bが終わった翌日から作業Dを行う。　　　　　　　　　　　　　　　　　　　　　　②作業Fが終わった翌日から作業Aを行う。　　　　　　　　　　　　　　　　　　　　③作業Bは2日間とも作業Eと同時に行う。　　　　　　　　　　　　　　　　　　　　　　④作業Cは3日間とも作業Fと同時に行う。　　　　　　　　　　　　　　　　　　　　　　　⑤1日の作業人数が3人になる日が1日だけある。　　　　　　　　　　　　　　　　　　　　　　作業Eに先行して作業D、作業Dに先行して作業Cを行わなければならないので、C→D→Eの順で、これで3＋2＋2＝7日間です。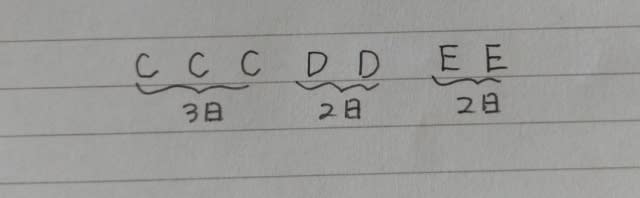

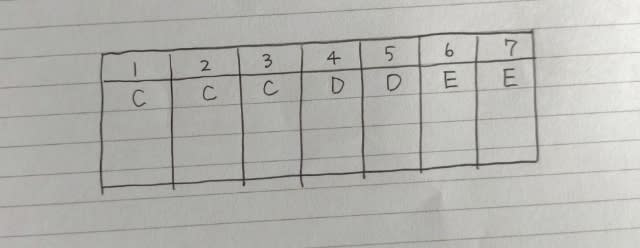作業Fは6日かかるので、Ⅰ、Ⅱのどちらかです。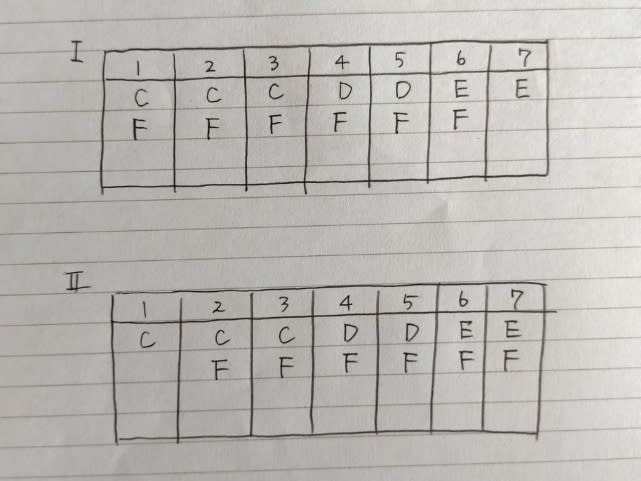
作業人数も考えて、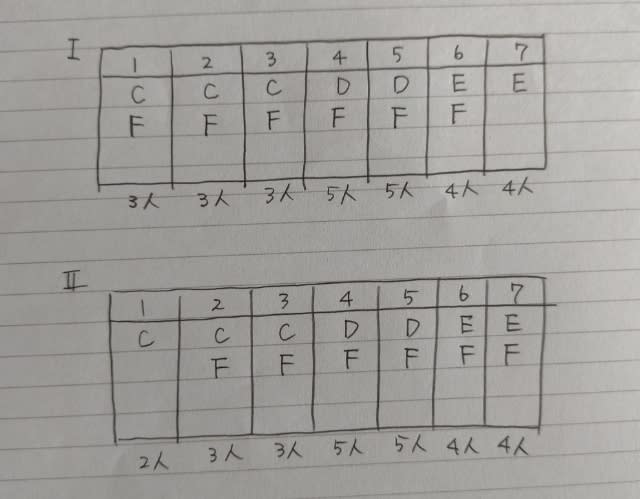　　　　　　　　　　　　　　　　　ところが、Ⅰは、早くもアウト！　　　　　　　　　　　　　作業Aができません。（作業Aは3人必要だから、どこに入れても作業人数が5人を超えてしまう）　　　　　　　　　　　　　　　　　　　　どうやら作業Aは、Ⅱの1日目にするしかありませんね。　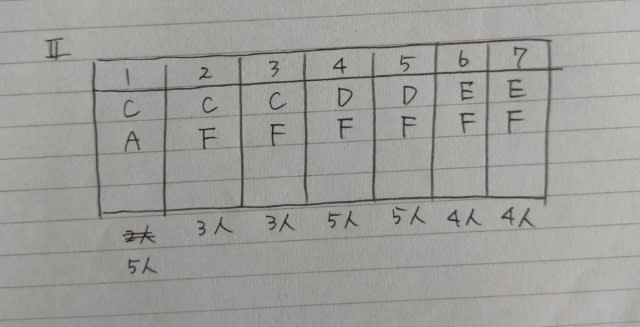　　　　　　　　　　　　　　　　残る作業Bは、人数からして2日目と3日目です。（Bは2人）
正解は、肢①です。

地方上級の判断推理 4

2021年出題。　　　　　　　　　　　　　　　　　　　　　　A〜Eの5人が青果店でトマト、レタス、にんじん、セロリの4種類のうち、何種類かの野菜を買った。　　　　　　　　　　　　　　　　　　　　　　4種類のうち、5人が買った野菜について次のことが分かっているとき、正しく言えるのはどれか。　　　　　　　　　　　　　　　　　　　・4種類のうち、Aは3種類、Bは2種類、Cは2種類を買った。　　　　　　　　　　　　　　　　　　　　・Cはにんじんを買い、Dはセロリを買った。　　　　　　　　　　　　　　　　　　　　　　　　・にんじんを買った人は5人のうち3人であった。　　　　　　　　　　　　　　　　　　　　　　・にんじんとセロリの両方を買った人は1人だけであった。　　　　　　　　　　　　　　　　　　　　　・レタスを買った人は2人だけであり、トマトを買った人はその2人にEを加えた3人であった。　　　　　　　　　　　　　　　　　　　①Aはセロリを買った。　　　　　　　　　　　　　　　　　②Bはにんじんを買った。　　　　　　　　　　　　③4種類の野菜のうち、Dは2種類を買った。　　　　　　　　　　　　　　　　④4種類の野菜のうち、Eは2種類を買った。　　　　　　　　　　　　　　　　　　　　　⑤セロリを買ったのは5人のうち3人であった。　　　　　　　　　　　　　　　　　　　　　　　ざっと表に条件を入れます。
最後の条件は、こういうことですね。よって、
トマトもレタスも両方買った人が2人いるのですが、それはCではありません。　　　　　　　　　　　　　　　　　　　　　　　Cはにんじんと、もう一つの2種類しか買っていないからです。


ってことは、Cはにんじんとセロリを買い、4つ目の条件に出てくる「にんじんとセロリの両方を買った人」はCのことであり、それ以外の人はにんじんとセロリを買っちゃだめだから、Dはにんじんを買っていない。　　　　　　　　　　　　　　　　　　　ここで、トマトとレタスの図を見て下さい。　　　　　　　　　　　　　　　　　　　　　　　　CとE以外の人は、両方買ったか、両方買わなかったかのどちらかです。　　　　　　　　　　　　　　Aは3種類買ったのだから、前者です。


Bがトマトもレタスも買わなかったらどうでしょうか?　　　　　　　　　　　　　　　　　　　　　　にんじんとセロリを買うことになる。　　　　　　　　　　　　そうすると4つ目の条件「にんじんとセロリの両方を買った人は1人」という条件に違反します。　　　　　　　　　　　　　　　　　　　なので、


にんじんを買った3人はA、C、E。　　　　　　　　　　　　　　Aは3種類だからセロリは買わない。
またもや4つ目の条件より、Eはセロリを買わない。　　　　　　　　　　　　　　　　　　　　　　　これで完成です。
肢①‥‥Aはセロリを買っていない。　　　　　　　　　　　肢②‥‥Bはにんじんを買っていない。　　　　　　　　　肢③‥‥Dは1種類しか買っていない。　　　　　　　　　　　肢⑤‥‥セロリを買ったのは2人。　　　　　　　　　　　　　　正解は肢④です。

地方上級の判断推理 3

2021年出題。　　　　　　　　　　　　　　　　　　　　　青、白、黄、緑、ピンク、オレンジの6色の同じ大きさの立方体の積み木がある。　　　　　　　　　　　　　　　その積み木が各色1個ずつ入ったセットが3つあり、春子ちゃん、夏子ちゃん、冬子ちゃんの3人が、各々1セット分の積み木6個を真っすぐ積み上げて、全部で3本の塔を作った。　　　　　　　　　　　　　　　　　　　　　　　　3人の積み木の積み方について次のことがわかっているとき、確実に言えるのはどれか。　　　　　　　　　　　　　　　　　　　　　　　　　・春子ちゃんは青を一番下に積み、冬子ちゃんは青を一番上に積んだ。　　　　　　　　　　　　　　・3人とも、黄の2個下に緑を積んだ。黄を積んだ位置は3人とも異なっていた。　　　　　　　　　　　　・白を積んだ位置は3人とも同じであった。　　　　　　　　　　　　　　　　　　　　　　　・ピンクを積んだ位置は3人とも異なり、春子ちゃんの一つ上が夏子ちゃん、夏子ちゃんの一つ上が冬子ちゃんであった。　　　　　　　　　　　　　　　　　　①春子ちゃんは、黄と緑の間にオレンジを積んだ。　　　　　　　　　　　　　　　　　　　　　②夏子ちゃんは、黄と緑の間に青を積んだ。　　　　　　　　　　　　　　　　　　　　　　　　　　③冬子ちゃんは、緑を下から2番目に積んだ。　　　　　　　　　　　　　　　　　　　　　　　　④春子ちゃんが積んだオレンジと夏子ちゃんが積んだピンクは同じ高さであった。　　　　　　　　　　　　　　　　　　　　　　　　　　⑤夏子ちゃんが積んだ黄と冬子ちゃんが積んだピンクは同じ高さであった。　　　　　　　　　　　　はじめの条件より、　　　　　　　　　　　　　　　　　　最後の条件より、（Ⅰ）、（Ⅱ）のどちらかです。

（Ⅰ）からやってみます。　　　　　　　　　　　　　　　3つ目の条件（白を積んだ位置は3人とも同じ）より、3人とも上から2番目に白を積んでいます。ここに、2つ目の条件（黄の2個下が緑）を入れます。春子と冬子は決定。夏子の黄は、一番上か上から3番目ですが、「黄を積んだ位置は3人とも異なっていた」という条件があるので、夏子の黄は上から3番目。空いているところに残っている色を入れて完成。選択肢は、④と⑤に絞られます。　　　　　　　　　　　　　　　　　次に（Ⅱ）の場合。　　　　　　　　　　　　　　　　　　　3つ目の条件より、白は下から2番目。
2つ目の条件より、春子と冬子の黄、緑は決定。
同じく2つ目の条件より、黄色は3人とも異なる位置だから、夏子の黄は上から2番目。　　　　　　　　　　　　　　　　　　　　　　　　春子と冬子の空いているところに残っているオレンジを入れて、
夏子の青とオレンジは入れかえ可。
結局、2通りあり得ます。


どちらにも共通する選択肢を探します。正解は、肢⑤です。

地方上級の判断推理 2

2021年出題。　　　　　　　　　　　　　　　　　　　　　　　身長の異なるA〜Fの6人がいる。　　　　　　　　　　　　この6人のうちから何人かを選び、身長の高い順に並んでもらい、高い方から数えて奇数番目の人だけに手を挙げてもらうようにした。　　　　　　　　　　　　　　　　　　　　　A、B、C、D、Eの5人の中では、A、B、Dが手を挙げ、B、C、D、E、Fの5人の中では、B、D、Fが手を挙げ、A〜Fの6人の中では、A、B、Cが手を挙げた。　　　　　　　　　　　　　　　　このとき、正しく言えるのはどれか。　　　　　　　　　①AはBよりも身長が高い。　　　　　　　　　　　②BはEよりも身長が高い。　　　　　　　　　　　　③CはFよりも身長が高い。　　　　　　　　　　　　　④DはCよりも身長が高い。　　　　　　　　　　　　　⑤FはEよりも身長が高い。　　　　　　　　　　　　例え話から始めます。　　　　　　　　　　　　　　ア、イ、ウ、エ、オ、カの6人がいて、この順に身長が高いとします。　　　　　　　　　　　　　高い方から奇数番目の人が手を挙げるとすると、ア、ウ、オの3人が手を挙げています。　　　　　　　　　　　　　　　　　　　　　　　　手を挙げている人に○をつけておきますね。
　　　　　　　　　　　　　　　　　　　　　　　　　　　ここでウが離脱したら？
　　　　　　　　　　　　　　　　　　　　　　　　　　　　文字だけ縦に並べてみます。
　　　　　　　　　　　　　　　　　　　　　　　　何か気がつきましたか〜？　　　　　　　　　　　　　　そうです!　　　　　　　　　　　　　　　　　　　　　　　　　ウよりも身長が高いアとイには変化がなく、ウよりも身長が低いエ、オ、カは、手を挙げていた人は手を下ろし、手を挙げていなかった人は手を挙げました。　　　　　　　　　　　　　　　　　でも、これは、たまたま手を挙げていたウが離脱したからそうなっただけじゃないの?と思った人もいるでしょう。　　　　　　　　　　　　　　　　今度は、イが離脱したとする。
　　　　　　　　　　　　　　　　　　　　　　　　　この場合も同じですね。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　つまり、ある人が離脱すると、その人より上位の人には変化が起こらず、その人より下位の人には変化が起こる。　　　　　　　　　　　　　　　　　逆に言うと、変化が起こらなかった人は、離脱した人より上位、変化が起こった人は離脱した人より下位だったということですね。　　　　　　　　　　　　　　　　　　　　　　　では、本問です。　　　　　　　　　　　　　　　　　　　　　例えと同様、手を挙げている人は○で囲みます。　　　　　　　　　　　　　　　　　　　　　　6人全員並んでいたときにはA、B、Cが手を挙げていたが、Fが離脱するとA、B、Dが手を挙げていたので、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　Aが離脱すると、B、D、Fが手を挙げていたので、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　この2つをまとめると、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　全員が並んでいたときに、背の高いBとEのうち、Bが手を挙げていたのだから、Bが一番背が高い。　　　　　　　　　　　　　　　　　二番目がE。　　　　　　　　　　　　　　　　　　　　三番目はA、四番目はF。　　　　　　　　　　　　　　　　背の低いCとDのうち、Cが手を挙げていたのだから、五番目がCで六番目がDです。
　　　　　　　　　　　　　　　　　　　　　　　　　　　正解は、肢②です。　　　　　　　　　　　　　　　　　　Aが離脱したところだけ考えれば、BとEが1番2番で、はじめにBが手を挙げていたからBが一番。　　　　　　　　　　　　　　　　　　　　　じゃあ肢②が確実にいえるとなりますね。