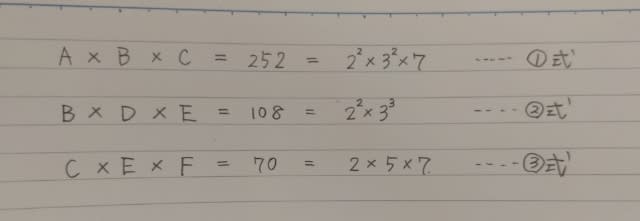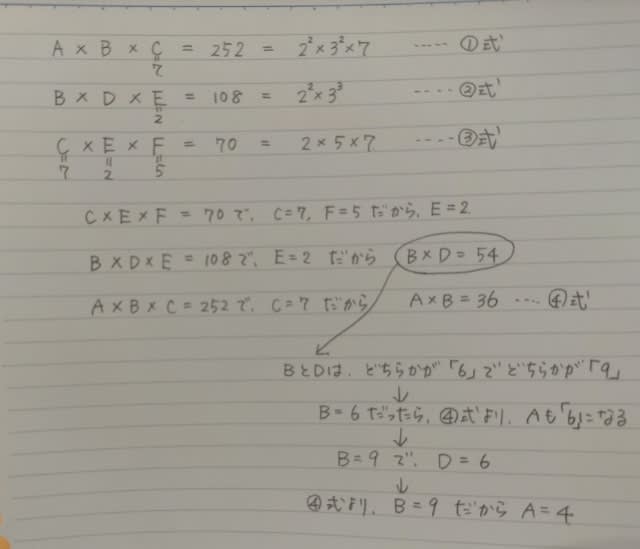あなたが生徒会長に立候補したとしましょう。 立候補者は、結構います。 結構じゃ現実味がないので、じゃあ7人いたとします。(2人以上いれば、何人でもこのお話しに関係ない) 全部で600票あるとして、さて、最低何票集めれば、確実に当選できるでしょうか? 答えは、301票です。 そりゃあ、500票くらいとれば、絶対当選しますよ! でも、最低何票かと聞かれたので、「500票くらい」というのは正解にはならないですね。 実際には、100票くらいでも当選するかもしれませんよ。 たとえば、
こんなことになるかもしれませんからねえ。 でも、確実に当選するかというと、そうとも限りません。 例えば、あなたが100票で、A君が500票で、その他が0票とか。 なんかややこしくなってきましたか? でも、よく考えると、「過半数」取ればいいのではないですか? 自分が過半数とっていれば、他がどうであろうが、絶対に当選ですし、もしぎりぎり過半数に到らないとき、つまり300票だったら、あなたが300票で、A君も300票で、他が0票だったら、決戦投票とか、じゃんけんとか、何らかの方法であなたが負けるかもしれません。 だから、もう一票必要。 つまり、301票以上とれば、あなたは確実に当選します。(301票以上取らないと当選できないという意味ではありません。 301票以上取れば、残りの299票がどの立候補者にどう流れていっても確実に当選するということ) ちょっとまとめます。 当選人数が1人のとき、投票数の2分の1より多く票を取れば当選確実です。 では、当選人数が2人のときはどうでしょうか? 正解は201票です。 200票獲得しても、ぎりぎり当選できないことがあります。 このときです。
3人で決戦投票かじゃんけんになります。(普通は立候補者は自分に1票入れるので、こういうことにはならないが) 201票あれば、自分以上のものが2人現れようとしたら投票数が603票以上必要になりますね。 少しそれますが、あなたが全くやる気のない立候補者で、自分で自分に投票することもせず、0票だったとします。 それでも、あなたは当選するかもしれません。 こういうこともあるからです。
当選者は2名ですから、A以外の人でじゃんけん。 じゃんけんですから、あなたの意志に反して勝っちゃったとか。 ここまでまとめますと、当選者数が1のとき、投票数の1/2より多く獲得すればOK。 当選者数が2のとき、投票数の1/3より多く獲得すればOK。 実は、これは当選者数が何でも同じことになって、当選者数がnのとき、投票数の1/(n+1)より多く獲得すれば当選確実になります。 では、練習問題ってか、2019年の海上保安学校の過去問です。 あるクラスには、44人の生徒がいる。 このクラスでは、今学期の体育の授業で行う競技を全生徒による投票で決めており、各生徒が8種目の中から一つだけ選んで1票ずつ投票する。 以下のA、Bの状況において、ある種目が「実施確実」となるのに最低必要な得票数の組合せとして最も妥当なのはどれか。 A:実施する競技が2種目 B:実施する競技が4種目 ただし、「実施確実」とは、他の種目の得票状況にかかわらず、Aの状況であれば上位2位以内、Bの状況であれば上位4位以内になると判断できることをいう。
Aの場合は、投票数(44票)の1/3より多く得票すればよい。 Bの場合は1/5より多く得票すればよいのだから、
正解は肢4ですね。 まとめ 当選確実=投票数×1/(n+1)より多。(割り切れるときは1を足す。)







こんなことになるかもしれませんからねえ。 でも、確実に当選するかというと、そうとも限りません。 例えば、あなたが100票で、A君が500票で、その他が0票とか。 なんかややこしくなってきましたか? でも、よく考えると、「過半数」取ればいいのではないですか? 自分が過半数とっていれば、他がどうであろうが、絶対に当選ですし、もしぎりぎり過半数に到らないとき、つまり300票だったら、あなたが300票で、A君も300票で、他が0票だったら、決戦投票とか、じゃんけんとか、何らかの方法であなたが負けるかもしれません。 だから、もう一票必要。 つまり、301票以上とれば、あなたは確実に当選します。(301票以上取らないと当選できないという意味ではありません。 301票以上取れば、残りの299票がどの立候補者にどう流れていっても確実に当選するということ) ちょっとまとめます。 当選人数が1人のとき、投票数の2分の1より多く票を取れば当選確実です。 では、当選人数が2人のときはどうでしょうか? 正解は201票です。 200票獲得しても、ぎりぎり当選できないことがあります。 このときです。

3人で決戦投票かじゃんけんになります。(普通は立候補者は自分に1票入れるので、こういうことにはならないが) 201票あれば、自分以上のものが2人現れようとしたら投票数が603票以上必要になりますね。 少しそれますが、あなたが全くやる気のない立候補者で、自分で自分に投票することもせず、0票だったとします。 それでも、あなたは当選するかもしれません。 こういうこともあるからです。

当選者は2名ですから、A以外の人でじゃんけん。 じゃんけんですから、あなたの意志に反して勝っちゃったとか。 ここまでまとめますと、当選者数が1のとき、投票数の1/2より多く獲得すればOK。 当選者数が2のとき、投票数の1/3より多く獲得すればOK。 実は、これは当選者数が何でも同じことになって、当選者数がnのとき、投票数の1/(n+1)より多く獲得すれば当選確実になります。 では、練習問題ってか、2019年の海上保安学校の過去問です。 あるクラスには、44人の生徒がいる。 このクラスでは、今学期の体育の授業で行う競技を全生徒による投票で決めており、各生徒が8種目の中から一つだけ選んで1票ずつ投票する。 以下のA、Bの状況において、ある種目が「実施確実」となるのに最低必要な得票数の組合せとして最も妥当なのはどれか。 A:実施する競技が2種目 B:実施する競技が4種目 ただし、「実施確実」とは、他の種目の得票状況にかかわらず、Aの状況であれば上位2位以内、Bの状況であれば上位4位以内になると判断できることをいう。

Aの場合は、投票数(44票)の1/3より多く得票すればよい。 Bの場合は1/5より多く得票すればよいのだから、

正解は肢4ですね。 まとめ 当選確実=投票数×1/(n+1)より多。(割り切れるときは1を足す。)


















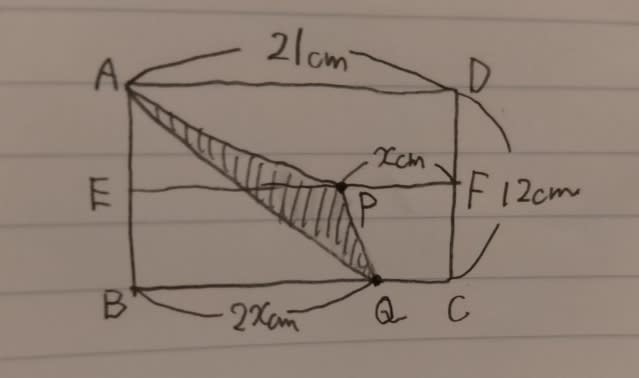
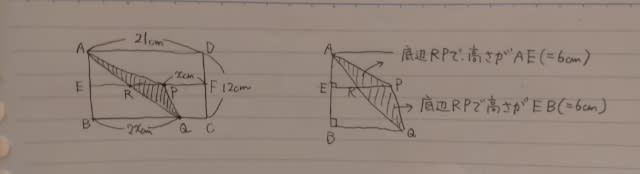











 A、B、Cが受け取った利息の比は、0.12a:0.1b:0.08cですが、これをできるだけ簡単にしましょう。
A、B、Cが受け取った利息の比は、0.12a:0.1b:0.08cですが、これをできるだけ簡単にしましょう。