下は割り算の筆算の一部を□で隠したものであり、□にはそれぞれ1桁の数字が入る。A、B、Cの和はいくらか。 ①20②21③22④23⑤24 九九の1の段、3の段、7の段、9の段の答えは、1の位がバラバラになっています。例えば、7の段の場合は、
①20②21③22④23⑤24 九九の1の段、3の段、7の段、9の段の答えは、1の位がバラバラになっています。例えば、7の段の場合は、 まず、無条件で決まるところは、
まず、無条件で決まるところは、 □7×Cをしたときに、1の位が9なので、Cは7しかありません。また、よくみると、丸で囲ったところには、6しか入りません。
□7×Cをしたときに、1の位が9なので、Cは7しかありません。また、よくみると、丸で囲ったところには、6しか入りません。 すると今度は、□7×Bをしたときに、1の位が6なので、B=8です。
すると今度は、□7×Bをしたときに、1の位が6なので、B=8です。 丸で囲った隣が3なので、割る数□7の□は6しかありません。
丸で囲った隣が3なので、割る数□7の□は6しかありません。 よって、下の方はどんどん決まっていきます。
よって、下の方はどんどん決まっていきます。 すると、三角で囲ったところには、2しか入らないのですから、A=6です。
すると、三角で囲ったところには、2しか入らないのですから、A=6です。 最後までやってみると、
最後までやってみると、 A+B+C=6+8+7=21。正解は、肢②です。ここをポチッとお願いします。→
A+B+C=6+8+7=21。正解は、肢②です。ここをポチッとお願いします。→
にほんブログ村

 ①20②21③22④23⑤24 九九の1の段、3の段、7の段、9の段の答えは、1の位がバラバラになっています。例えば、7の段の場合は、
①20②21③22④23⑤24 九九の1の段、3の段、7の段、9の段の答えは、1の位がバラバラになっています。例えば、7の段の場合は、 まず、無条件で決まるところは、
まず、無条件で決まるところは、 □7×Cをしたときに、1の位が9なので、Cは7しかありません。また、よくみると、丸で囲ったところには、6しか入りません。
□7×Cをしたときに、1の位が9なので、Cは7しかありません。また、よくみると、丸で囲ったところには、6しか入りません。 すると今度は、□7×Bをしたときに、1の位が6なので、B=8です。
すると今度は、□7×Bをしたときに、1の位が6なので、B=8です。 丸で囲った隣が3なので、割る数□7の□は6しかありません。
丸で囲った隣が3なので、割る数□7の□は6しかありません。 よって、下の方はどんどん決まっていきます。
よって、下の方はどんどん決まっていきます。 すると、三角で囲ったところには、2しか入らないのですから、A=6です。
すると、三角で囲ったところには、2しか入らないのですから、A=6です。 最後までやってみると、
最後までやってみると、 A+B+C=6+8+7=21。正解は、肢②です。ここをポチッとお願いします。→
A+B+C=6+8+7=21。正解は、肢②です。ここをポチッとお願いします。→にほんブログ村












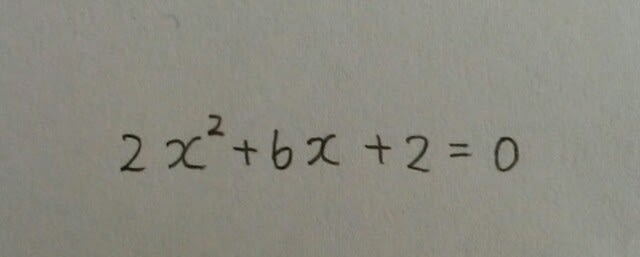 の解として正しいものを、次の1~4の中から1つ選びなさい。
の解として正しいものを、次の1~4の中から1つ選びなさい。 まず両辺を2で割って、
まず両辺を2で割って、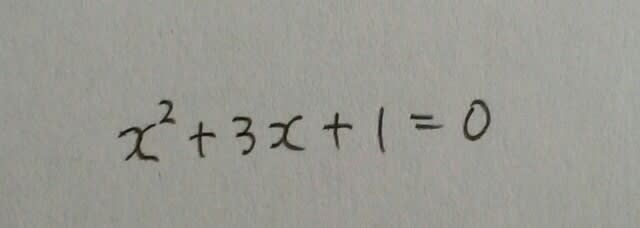 左辺は因数分解できないので、解の公式に当てはめます。
左辺は因数分解できないので、解の公式に当てはめます。
 正解は、肢2です。ここをポチッとお願いします。→
正解は、肢2です。ここをポチッとお願いします。→

 円に四角形が内接するとき、四角形の向かい合う角の和は180ºです。よって、∠DAF=70º。(正解は1か5)。
円に四角形が内接するとき、四角形の向かい合う角の和は180ºです。よって、∠DAF=70º。(正解は1か5)。 次に、AB=BC=CDという条件を使いましょう。 BとOをむすんで…。 AO、BO、COはこの円の半径で、長さは等しいので、△ABO≡△BCO≡△CDO。 よって、∠ABCの140ºは2等分されて、70ºずつになります。なので、
次に、AB=BC=CDという条件を使いましょう。 BとOをむすんで…。 AO、BO、COはこの円の半径で、長さは等しいので、△ABO≡△BCO≡△CDO。 よって、∠ABCの140ºは2等分されて、70ºずつになります。なので、 ∠CODは40º(正解は5)。中心角は、円周角の2倍ですから、∠DOF=140º。
∠CODは40º(正解は5)。中心角は、円周角の2倍ですから、∠DOF=140º。 よって、∠AOF=360-(40+40+40+140)=100ºです。
よって、∠AOF=360-(40+40+40+140)=100ºです。 すると、∠AGFは弧ADFの円周角だから、260÷2=130ºです。
すると、∠AGFは弧ADFの円周角だから、260÷2=130ºです。 ここをポチッとお願いします。→
ここをポチッとお願いします。→

 次のア~エが分かっているとき確実にいえるのはどれか。 ア スタートしてからゴールするまで順序が入れ替わることはない。 イ Aが最初にすれ違ったのはCであり、Cが最初にすれ違ったのはAである。 ウ Bが最後にすれ違ったのはFであり、Fが最後にすれ違ったのはBである。 エ Dが3番目にすれ違ったのはEであり、4番目にすれ違ったのはFである。 ①1番前はAである。 ②前から2番目はCである。 ③前から3番目はEである。 ④後ろから3番目はDである。 ⑤後ろから2番目はFである。 条件アより、この公式が使えます。 条件イより、CとAは共に1位か2位。 条件ウより、FとBは共に5位か6位。 条件エより、Eは3位か4位で、Fは4位か5位。 すると、Fは5位か6位でもあるし、4位か5位でもあるのだから、5位。正解は、肢⑤です。 もう少しやってみると、Fが5位と決まれば、自動的にBは6位。1位2位は、どちらがCでどちらがAかは決まりません。3位4位も、どちらがDでどちらがEか決まりません。 ここをポチッとお願いします。→
次のア~エが分かっているとき確実にいえるのはどれか。 ア スタートしてからゴールするまで順序が入れ替わることはない。 イ Aが最初にすれ違ったのはCであり、Cが最初にすれ違ったのはAである。 ウ Bが最後にすれ違ったのはFであり、Fが最後にすれ違ったのはBである。 エ Dが3番目にすれ違ったのはEであり、4番目にすれ違ったのはFである。 ①1番前はAである。 ②前から2番目はCである。 ③前から3番目はEである。 ④後ろから3番目はDである。 ⑤後ろから2番目はFである。 条件アより、この公式が使えます。 条件イより、CとAは共に1位か2位。 条件ウより、FとBは共に5位か6位。 条件エより、Eは3位か4位で、Fは4位か5位。 すると、Fは5位か6位でもあるし、4位か5位でもあるのだから、5位。正解は、肢⑤です。 もう少しやってみると、Fが5位と決まれば、自動的にBは6位。1位2位は、どちらがCでどちらがAかは決まりません。3位4位も、どちらがDでどちらがEか決まりません。 ここをポチッとお願いします。→