同じ大きさのひし形を組み合わせた6個の図形ア〜カがある。 これらのうち5個の図形を選んで、重なることなく、かつ裏返さずに並べると、下の図のような平行四辺形ができた。 カの図形が下図のような位置に配置される場合、5つの図形ア〜オのうち選ばれなかった図形はどれか。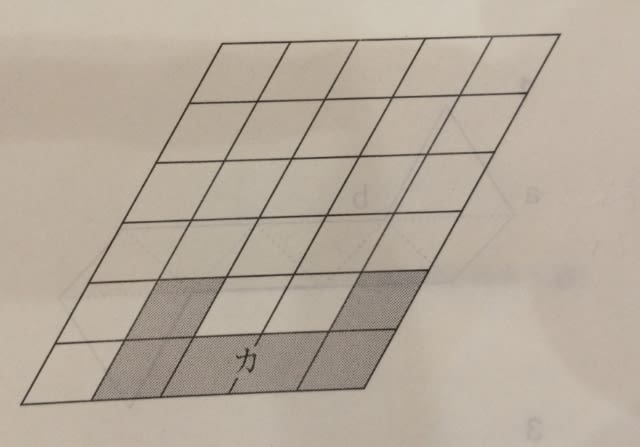
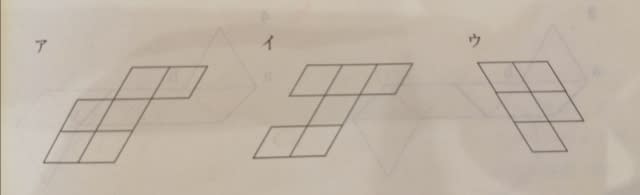
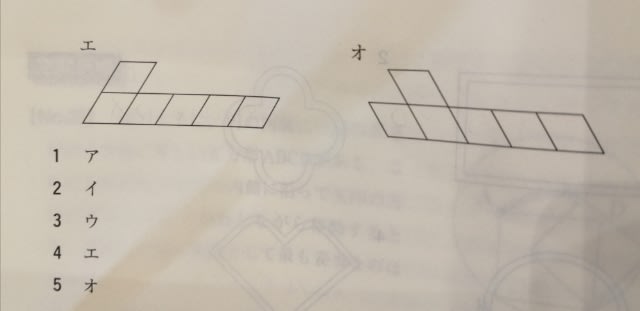
「裏返さずに」がポイントになりそうですが、な〜んも関係ありません。 全部で30マスあり、そのうちの6マスにカが配置されています。 残る24マスに、どのピースをどう配置するか? と真面目に考える前に、まずは数合わせですよね。 ア〜オまで全部で、6＋6＋5＋6＋6＝29マスあるので、なるほど全てのピースを入れる訳にはいきません。(残りが24マスしかない) すると、5マス分は不要。 じゃあ正解は肢3しかないでしょうということですねえ。 もう少し補足すると、例えば選ばれなかった図形がアだとしたら、イとウとエとオとカを選んだということですが、それでは6＋5＋6＋6＝23マスだから、どこかに1マス分の空白部分ができてしまいます。 選ばれなかった図形がイだとしてもエだとしてもオだとしても同じことですね。 えっ?やってみないとズルい?一例ですが、こんなふうになりました。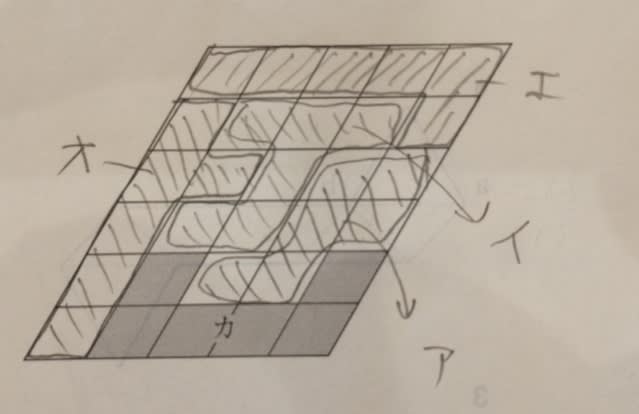
ここをポチッとお願いします。→
「裏返さずに」がポイントになりそうですが、な〜んも関係ありません。 全部で30マスあり、そのうちの6マスにカが配置されています。 残る24マスに、どのピースをどう配置するか? と真面目に考える前に、まずは数合わせですよね。 ア〜オまで全部で、6＋6＋5＋6＋6＝29マスあるので、なるほど全てのピースを入れる訳にはいきません。(残りが24マスしかない) すると、5マス分は不要。 じゃあ正解は肢3しかないでしょうということですねえ。 もう少し補足すると、例えば選ばれなかった図形がアだとしたら、イとウとエとオとカを選んだということですが、それでは6＋5＋6＋6＝23マスだから、どこかに1マス分の空白部分ができてしまいます。 選ばれなかった図形がイだとしてもエだとしてもオだとしても同じことですね。 えっ?やってみないとズルい?一例ですが、こんなふうになりました。
ここをポチッとお願いします。→
にほんブログ村
そんなの人によって答えはそれぞれ違うのですが、平面図形の問題を解いている人にとっては、「平行四辺形を6分の1と6分の5に分割している図」なのです。
では、これは何の図でしょう？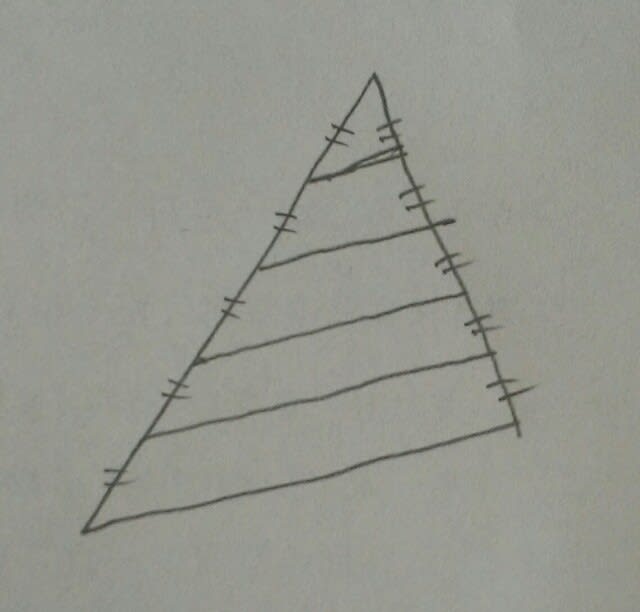
知るかよ～！とお思いになるかも知れませんが、平面図形の問題を解いている人にとっては、「三角形の面積を、1：3：5：7：9に分割している図なのです。小さい方から順に、奇数比になります。
このような感覚をお持ちの方は、本問は秒殺～！ 一辺の長さが1の正方形の各辺を4等分し、4等分した点の一つと頂点を、図のように線分で結んだとき、網掛け部分の図形の面積はいくらか。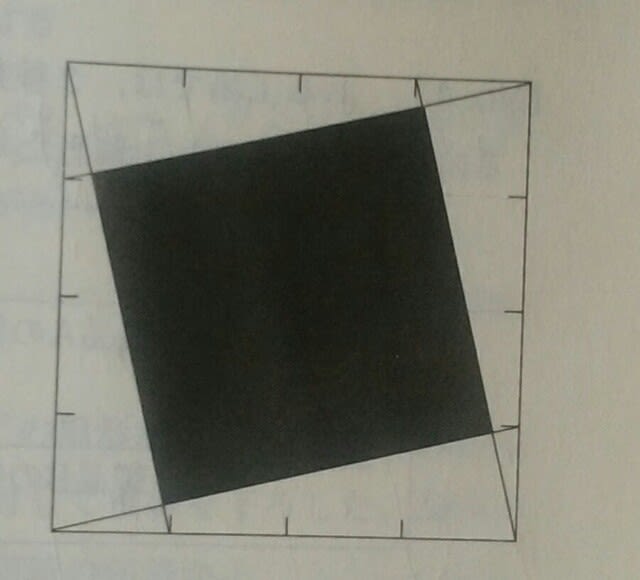
①9/17②7/13③10/17④8/13⑤11/17 要するに、こうなりますね。
ほんとうは、△ABCと△BCDと△DFGと△FHAが合同であること、区切り線が平行であることを証明しなければならないのですが、もう感覚的でやっていっても構いませんね。 今度は、△ABIが全体の1/8になっているので、こうなります。
問題の図の、白い部分は、（①＋③＋⑤＋⑦）×4です。よって、
正解は、肢①です。ここをポチッとお願いします。→
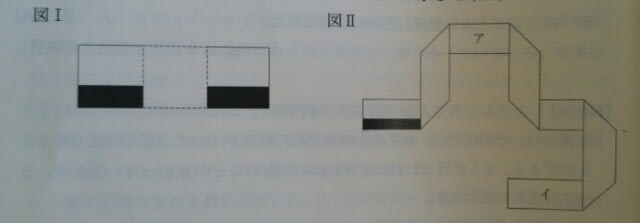
全て直角に折り曲げられています。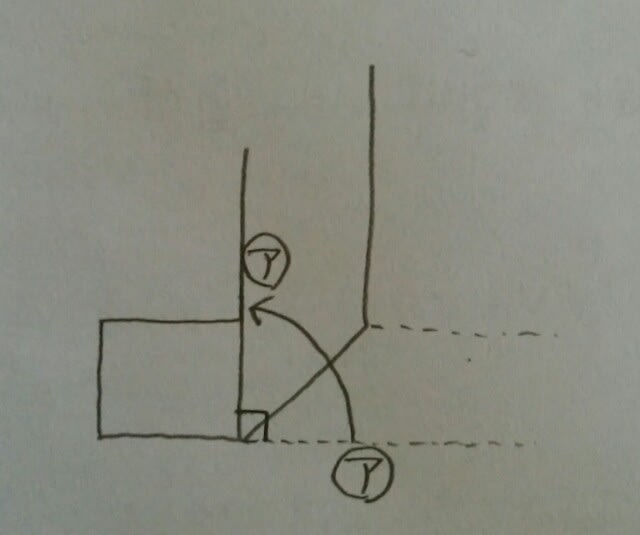
よって、黒い太線も、直角に曲がっていきます。黒い太線は、紙の下側にあるので、下側の縁がどこにあるのかを追跡しましょう。
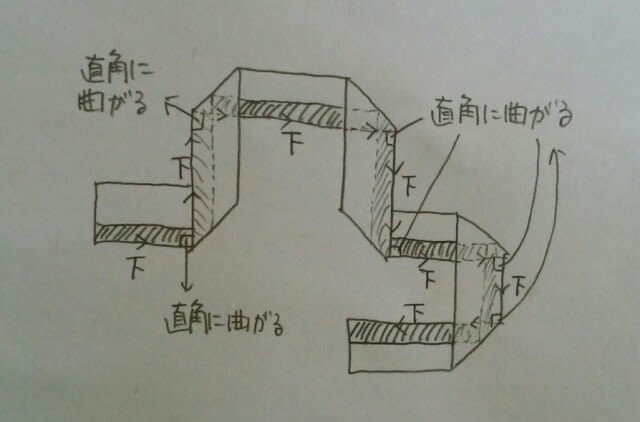ということで、正解は、肢4です。ここをポチッとお願いします。→
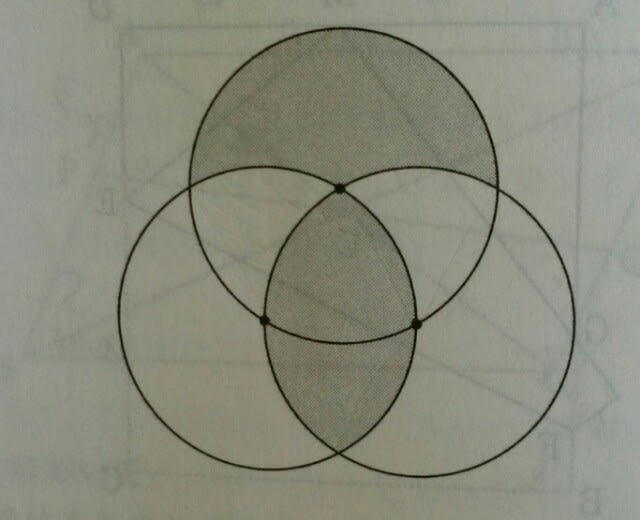（三重県教員採用試験） 出した物は出しっぱなし、授業で使ったプリントも、どこかへいってしまって、次の授業前、「あのプリントどこや？」と探しまくって、結局出てこない。ホントに情けなくなります。（私のこと） なので、こういう問題は苦手です。斜線部分を、矢印で示した場所にお片づけ～。
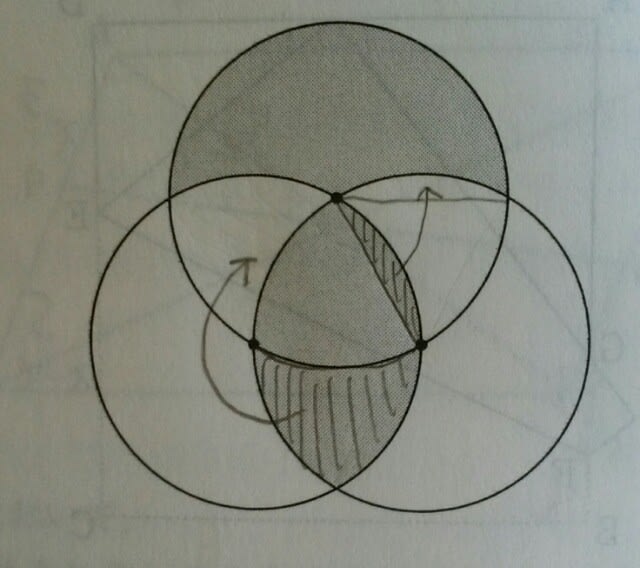すると、
すっきりり～ん。
r1とr2は、上の円の半径、r3は、右下の円の半径で、全ての円の半径は等しいのだから、r1＝r2＝r3。パックマンのお口は60º開いています。よって、求める面積は、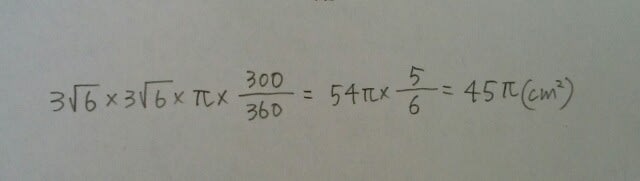
正解は、45π㎠です。ここをポチッとお願いします。→
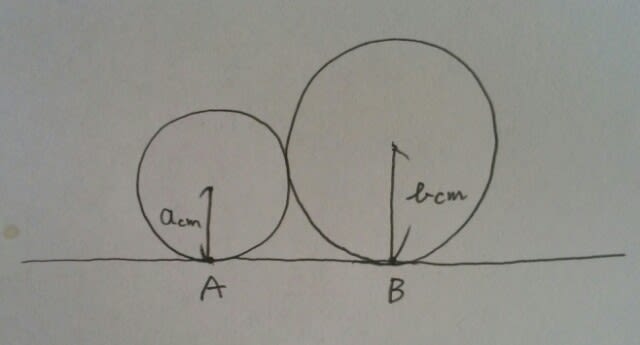さて、線分ABの長さはいくらになるでしょうか？以前、図形の３つの手筋を紹介しましたが、円と接線があれば、円の中心と接点を結ぶ（すると90°になる）。円や球が外接していれば、中心どうしを結ぶのでした。
O1からO2Bに垂線をおろして、その交点をCとします。
四角形O1ABCは、３つの角が90°なので、もう一つの角も90°になり、長方形です。長方形は、向かい合う辺の長さが等しいので、AB＝O1Cです。
O2C＝O2B－CB＝b－a。△O2O1Cは、直角三角形なので、三平方の定理より、
こ～んなにきれいにまとまっちゃうので、これは公式として覚えておけば、とても役にたちますよ。 例えば、平成29年国家一般職（大卒）より。 図のように、円A、B、Cと直線lが互いに接している。円Aと円Bの半径が等しく、また、円Cの半径が2であるとき、円Aの半径はいくらか。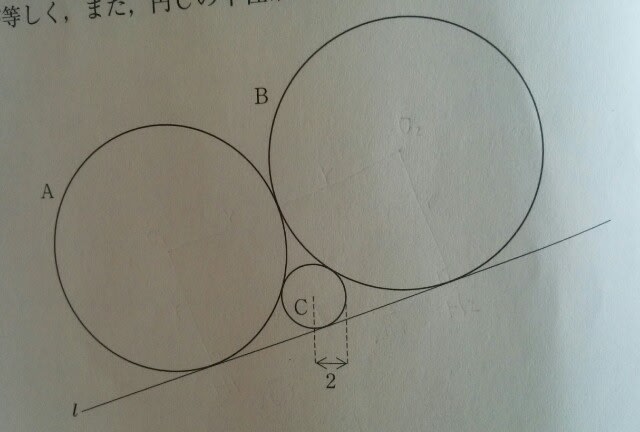
①4√3②7③8④6√2⑤9 円Aと円Bの半径をrとすると、
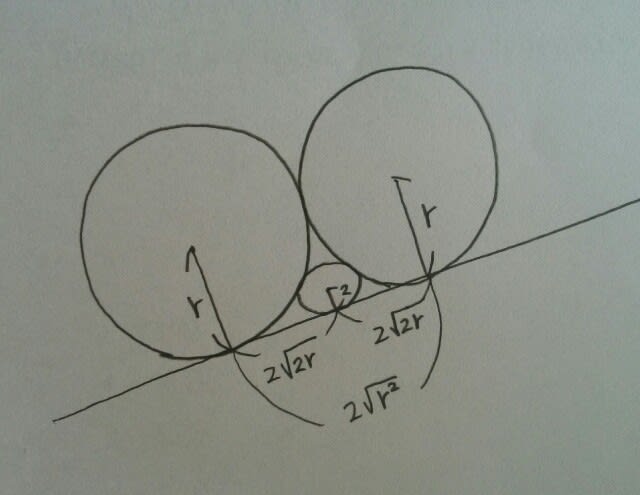よって、
正解は、肢③です。 もういっちょう～。平成22年地方上級より。次の図のように、半径3cmの円と半径6cmの円が点Cで接している。2つの円に接する3本の接線の交点をO、A、Bとするとき、ABの長さはどれか。
①3√6cm②6√2cm③9cm④4√6cm⑤6√3cm 円外の1点から引いた2つの接線の長さは等しいので、
ってな具合で、正解は、肢②です。ここをポチッとお願いします。→