図Ⅰのように、幅が一定の紙テープを用いて同じ大きさの輪を二つ作り、図Ⅱのように、二つの輪が直交するようにこれらを面で接着した。この接着した二つの輪を、その中央線(図Ⅱの点線)に沿って切り開いたとき、できる図形として最も妥当なのはどれか。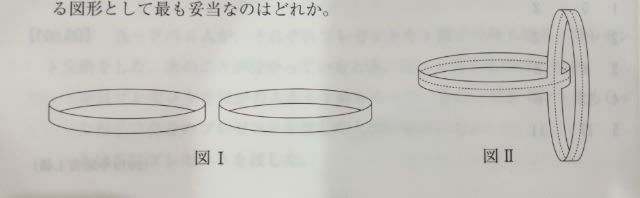
ここがポイントです。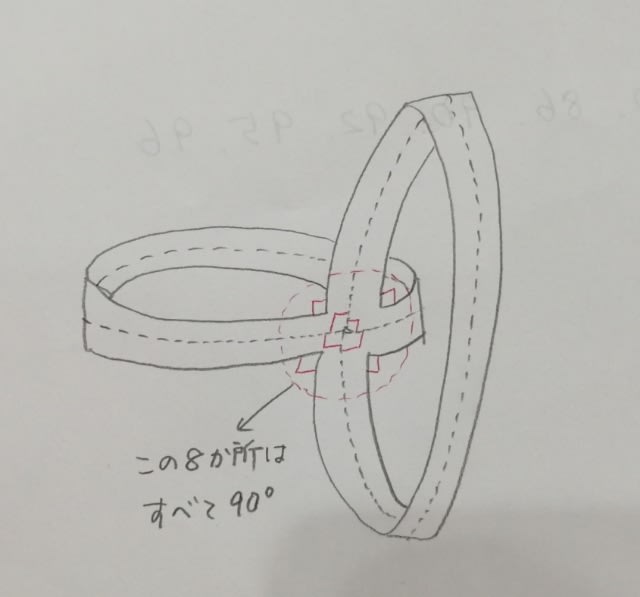
切り開くと、(ちょっとだけよ〜ん)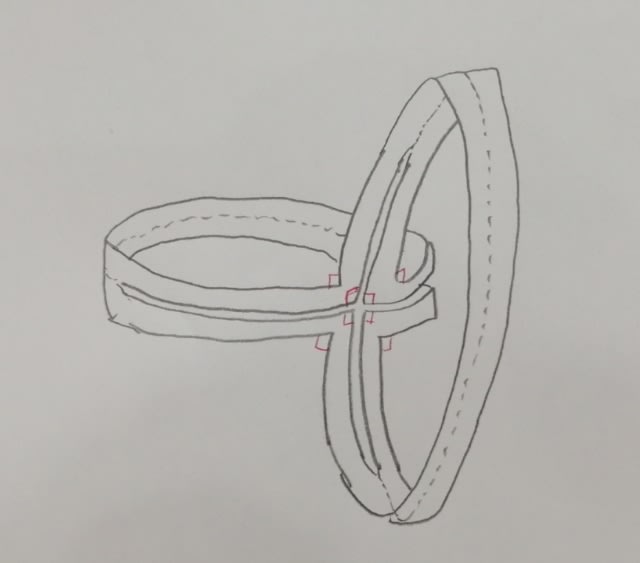
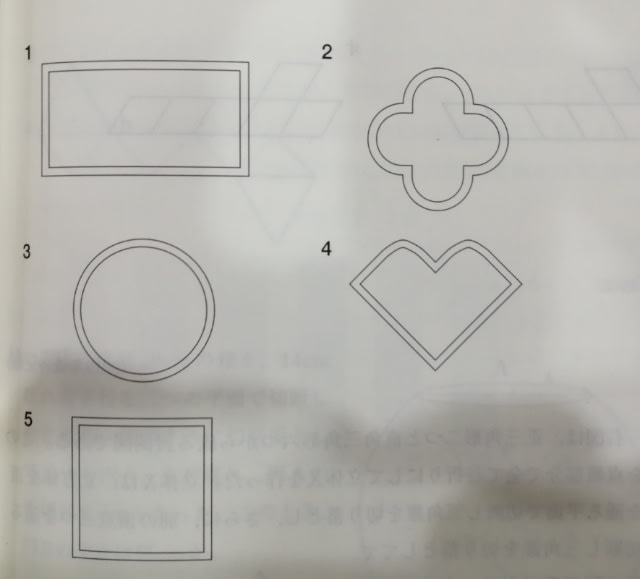
ということだけ確認できれば、正解は肢1か肢5ですね。 同じ大きさの輪だから、たぶん肢5だなくらいで十分正解です。一応確認します。 この輪の円周(長さ)が仮に10cmだとします。そしてあなたは小さな虫です。黒い点の位置から、真っ直ぐに進んで下さい。ちょうど10㎝進むと、曲がり角にきますね。そこであなたは右へ90度曲がらなければいけません。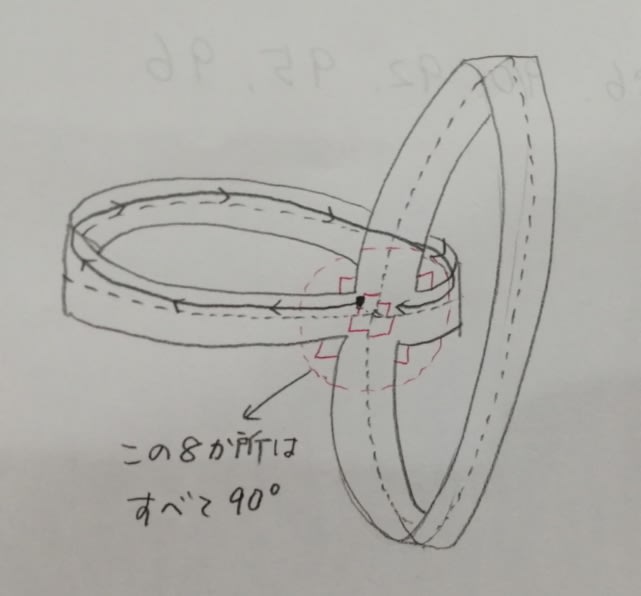
そして、また10cm直進すると右へ90度曲がり、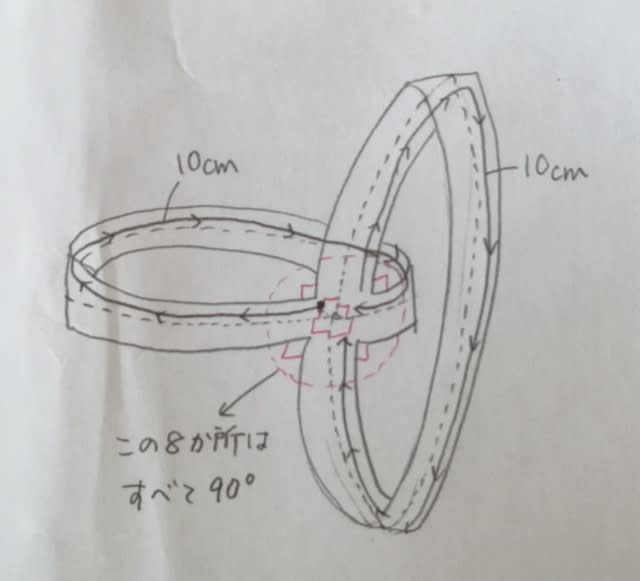
これを4回続けると元の場所に戻ってきます。だから、正方形ができます。正解は、肢5です。ここをポチッとお願いします。→


ここがポイントです。

切り開くと、(ちょっとだけよ〜ん)

ということだけ確認できれば、正解は肢1か肢5ですね。 同じ大きさの輪だから、たぶん肢5だなくらいで十分正解です。一応確認します。 この輪の円周(長さ)が仮に10cmだとします。そしてあなたは小さな虫です。黒い点の位置から、真っ直ぐに進んで下さい。ちょうど10㎝進むと、曲がり角にきますね。そこであなたは右へ90度曲がらなければいけません。

そして、また10cm直進すると右へ90度曲がり、

これを4回続けると元の場所に戻ってきます。だから、正方形ができます。正解は、肢5です。ここをポチッとお願いします。→
にほんブログ村













 図Bを利用して、
図Bを利用して、 この時に、注意することが2つあります。それは、
この時に、注意することが2つあります。それは、 だから、広げると、
だから、広げると、 では、次に、図Bや図Cの場所を確認します。
では、次に、図Bや図Cの場所を確認します。 正方形の紙の右上ですね。選択肢を見ましょう。
正方形の紙の右上ですね。選択肢を見ましょう。 ここをポチッとお願いします。→
ここをポチッとお願いします。→

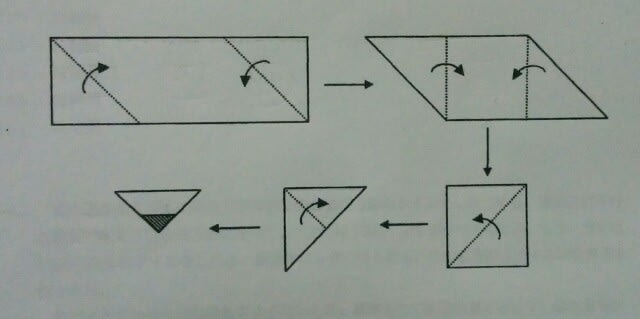
 最後の状態から、1つずつ元に戻していきます。斜線部は、欠けている部分(切り落とした部分)です。
最後の状態から、1つずつ元に戻していきます。斜線部は、欠けている部分(切り落とした部分)です。 次に、
次に、 その次に、
その次に、 そして、
そして、 よって、正解は、肢1です。
よって、正解は、肢1です。
 ア 頂点Aと頂点Cが重なるように折った後、頂点Bと頂点Dが重なるように折る。 イ 直線BDで折った後、頂点Aと頂点Cが重なるように折る。
ア 頂点Aと頂点Cが重なるように折った後、頂点Bと頂点Dが重なるように折る。 イ 直線BDで折った後、頂点Aと頂点Cが重なるように折る。 アについて。AとCが重なるように折ったときの折り目は、線分ACの垂直二等分線です。
アについて。AとCが重なるように折ったときの折り目は、線分ACの垂直二等分線です。
 次に、BとDが重なるように折るので、線分BDの垂直二等分線を折り目として折ります。
次に、BとDが重なるように折るので、線分BDの垂直二等分線を折り目として折ります。 イについて。BDで折ると、
イについて。BDで折ると、 次にAとCが重なるように折るので、
次にAとCが重なるように折るので、 テストでは、コンパス等は使用できませんので、だいたいの作図しかできませんが、アもイも、最後は四角形になるということさえ分かれば、面積は関係なしに、肢5しかありません。お手元の紙を自分で折って、確かめて下さい。
テストでは、コンパス等は使用できませんので、だいたいの作図しかできませんが、アもイも、最後は四角形になるということさえ分かれば、面積は関係なしに、肢5しかありません。お手元の紙を自分で折って、確かめて下さい。