半径10cmの球を、14cm離れた平行な二つの平面で切断したところ、図のように切断面として二つの円A、Bが現れ、円Aの半径は6cmとなった。このとき、円Bの半径は何cmか。
こういうことですね。
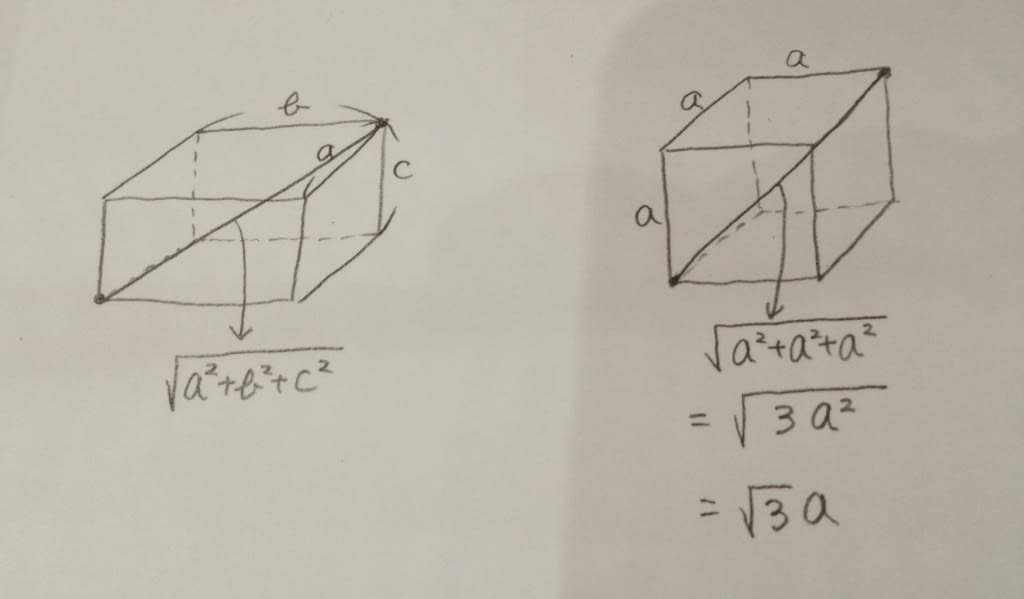
おっ!３対４対５の直角三角形が二つあるから、正解は８cmね。 これで分かった人はここから先は読み飛ばして下さい。 まずは、図形の問題でよく出てくる直角三角形４つを覚えておかなければならないのですが、そのうちの一つ。
③、④、⑤のうちの二つの辺の比がこれに当てはまれば、もう一つの辺の長さが分かります。たとえば、
ええ、ええ、もちろん、３平方の定理を使っても構いませんよ。でも、計算するのがちょっと面倒ですね。
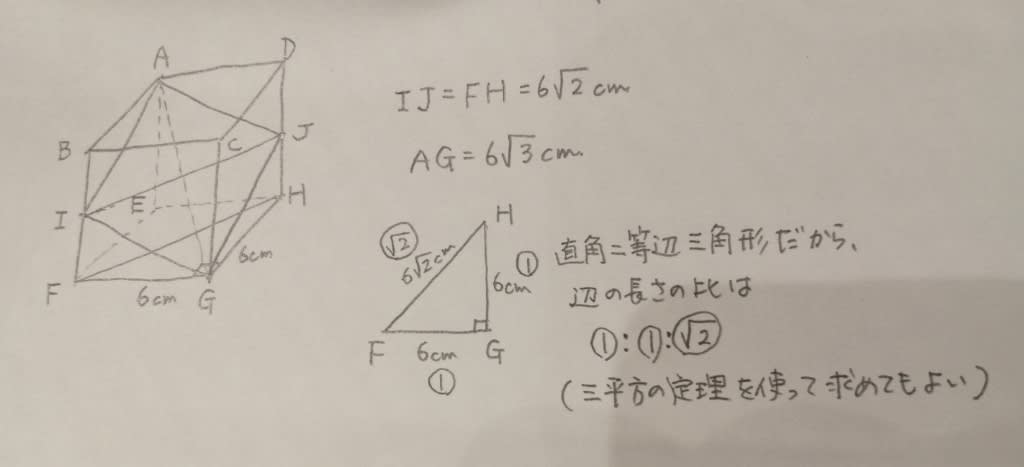
本問では、こうなっています。
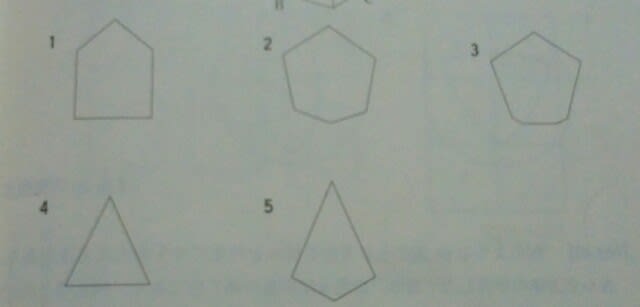
正解は、肢2です。ここをポチッとお願いします。→
にほんブログ村
こういうことですね。
おっ!３対４対５の直角三角形が二つあるから、正解は８cmね。 これで分かった人はここから先は読み飛ばして下さい。 まずは、図形の問題でよく出てくる直角三角形４つを覚えておかなければならないのですが、そのうちの一つ。
③、④、⑤のうちの二つの辺の比がこれに当てはまれば、もう一つの辺の長さが分かります。たとえば、
ええ、ええ、もちろん、３平方の定理を使っても構いませんよ。でも、計算するのがちょっと面倒ですね。
本問では、こうなっています。
正解は、肢2です。ここをポチッとお願いします。→
にほんブログ村
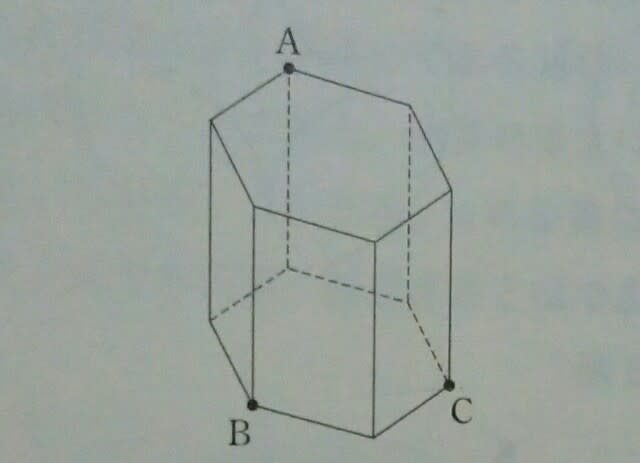
点BとCは、同じ平面上なので、線で結びます。AとB、AとCは同じ平面上にはありません（2点を結ぶと立体の内部を通る）ので、絶対に結んではいけません。
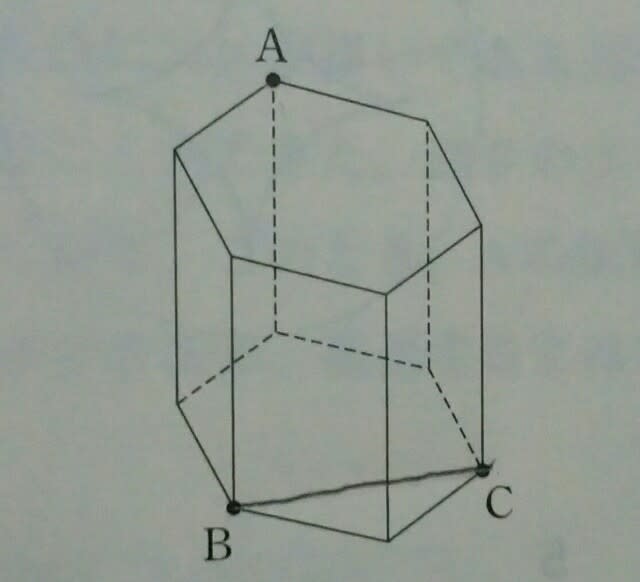アの面とイの面とは平行なので、切り口と切り口が平行になります。
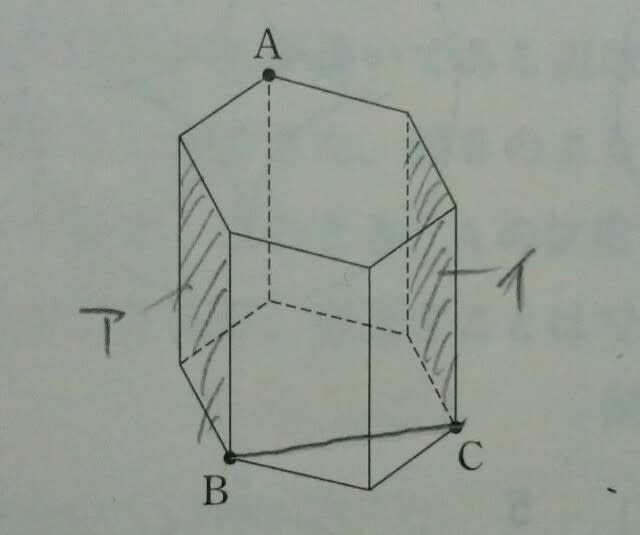今、点Aなど無視して、適当に切ってみましょう。
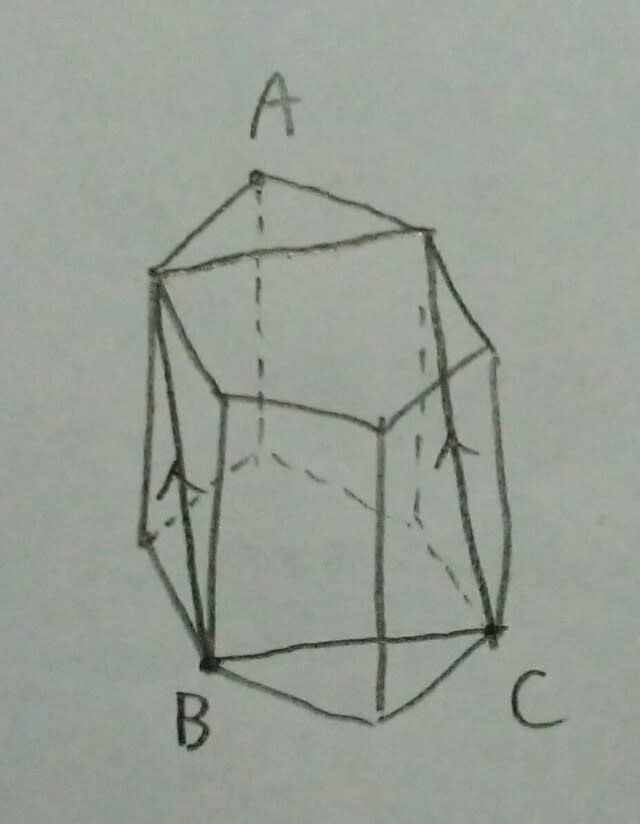こんなのは、Aを通らないので、もちろんダメ。では、点Aを通るためには、どうすればいいのでしょうか？こんな感じですね。
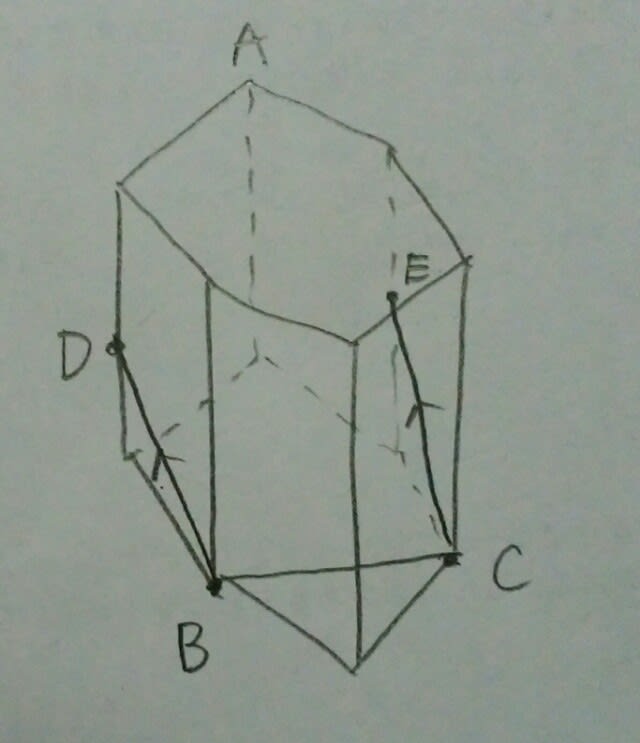AとD、AとEは、同じ平面上なので、線で結んで出来上がり。
正解は、肢①です。ここをポチッとお願いします。→
下の図は、正八面体であり点A、B、Cは、各辺の中点である。この正八面体を、点A、B、Cを含む平面で切断し、頂点Pを含む立体を矢印の方向から見たときの図として、最も妥当なのはどれか。
切断のポイントは、①同じ平面上の2点は、直線で結ぶ。（同じ平面上ではないときは、絶対に結ばない）②平行な面を探す。基本的にこの2つだけです。AとBは、同じ平面上だから、結びます。
下の図で、赤で囲った面と、緑で囲った面は平行ですから、切り口の線同士も平行になります。
はい、ここでネタ切れです。もうこれ以上は、テクニックでどうのこうのではなくなりました。こんな図を、頭に入れておかなくてはいけません。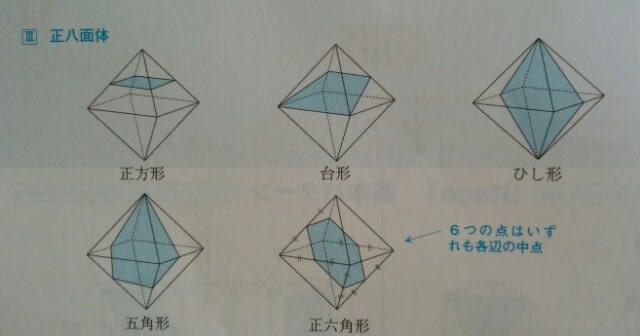
最後の図をよく見ると、平行な面同士に、平行な線が入っていますね！図が小さく、本問と向きが違うので、もう一度。
要するに、正八面体の切断で、平行な面に、平行な線が入れば、切り口は六角形になり、それが辺の中点であるときは、切り口は正六角形なのです。さて、点Pを含む立体を調べます。画面の左上の立体を取り除けばいいですね。
これを正面から見ると、上に正六角形、下に小さな三角形が見えます。こんな感じです。
よって、正解は、肢①です。
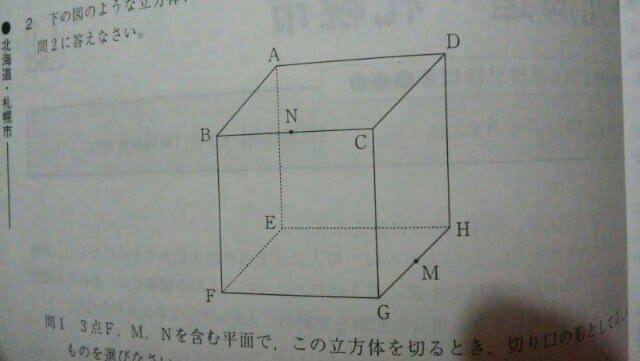問1 3点F、M、Nを含む平面で、この立方体を切るとき、切り口の形として正しいものを選びなさい。 ア、正三角形 イ、二等辺三角形 ウ、長方形 エ、平行四辺形 オ、台形 問2 頂点Fを出発して立方体の辺の上を動く任意の点Pが、同じ頂点を2度通らず、かつ、点M、Nを通ることなく頂点Dまで移動する場合、行き方は全部で何通りか、正しいものを選びなさい。 ア、3通り イ、4通り ウ、5通り エ、6通り オ、7通り 問1。同じ平面上の2点が出てきたら、その2点をまっすぐ結ぶ。同じ平面上の点ではないときは、絶対に結ばないで下さい。 本問では、FとNは、同じ平面上なので結び、FとMも、同じ平面上なので結びます。MとNは、違う面上にあるので結んではいけません。
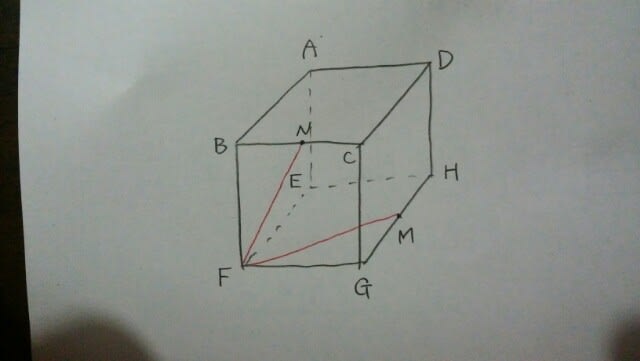面と面が平行ならば、切り口と切り口も平行です。この立方体が透明な素材でできていると思って、真上から見ると、
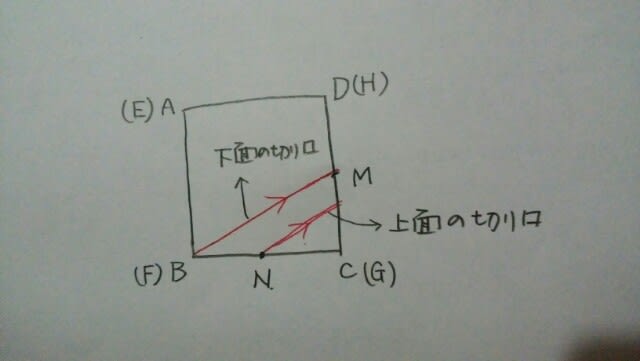よって、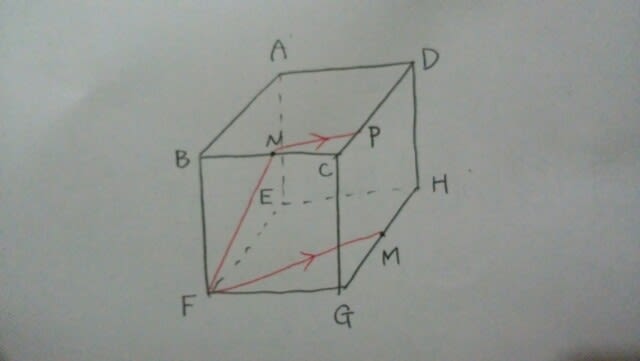
PとMは、同じ平面上なので、まっすぐ結びます。
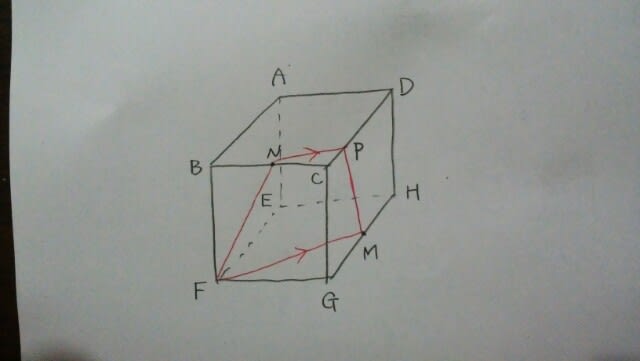よって、オが正解。 問2 どうせNとMは通れないのだから、辺BCと辺GHは消してしまいましょう。
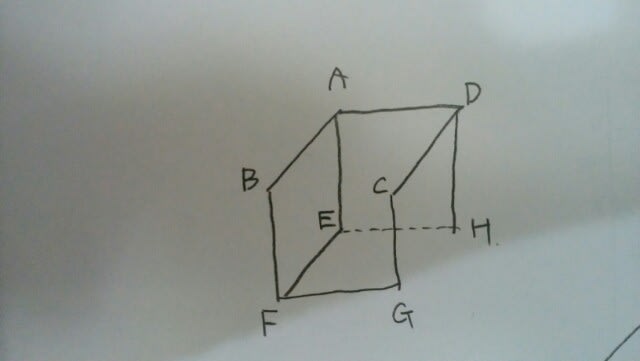この状態で、同じ頂点を2度通らないようにしてDまで行きます。樹形図をかくといいですね。
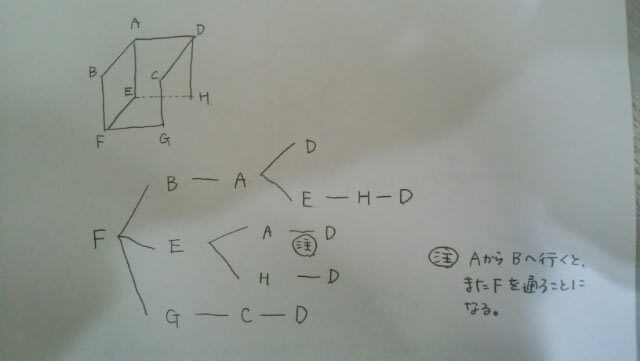よって、正解はウです。