地方初級の数的推理 6

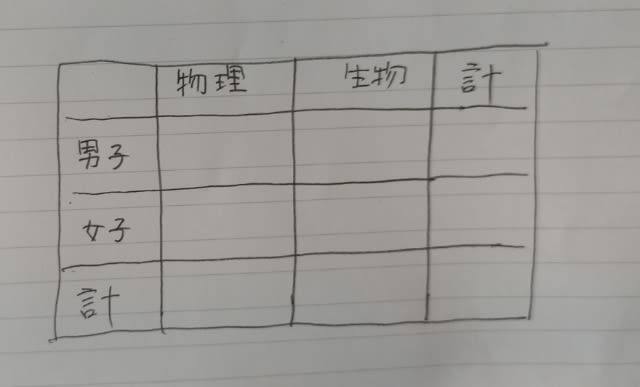
2012年出題。　　　　　　　　　　　　　　　　　　　　　　　三つの正の整数a,b,cが次の条件を満たすとき、a+b+cはいくらか。　　　　　　　　　　　　　　　　　　　　　　・a<b<c<10である。　　　　　　　　　　　　　　　　　　　　　　　　　　・aは奇数である。　　　　　　　　　　　　　　　　　　　　　　　　・bとcの差は3である。　　　　　　　　　　　　　　　　　　　　　　　　・aとcの平均は、bより小さい整数である。（選択肢省略）　　　　　　　　　　　　　　　　　　　　　a<b<c<10で、aは奇数だから、a、b、cに適当な整数を当てはめていけば、何とかなる問題です。　　　　　　　　　　　　　　　　　　　　　　　でも、ここでは、真面目に考えていきます。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　奇数+奇数=偶数で、奇数+偶数=奇数というのは大丈夫ですね～。　　　　　　　　　　　　　　　　　　　　もしもcが偶数だったら、aとcの平均は整数になりません。　　　　　　　　　　　　　　　　　　　　　　例えば、a=1、c=8だとすると、aとcの平均は4.5となって、最後の条件を満たすことができません。　　　　　　　　　　　　　　　　　　　　　　だから、cは奇数です。　　　　　　　　　　　　　　　　　　　　そして、この最後の条件を図にすると、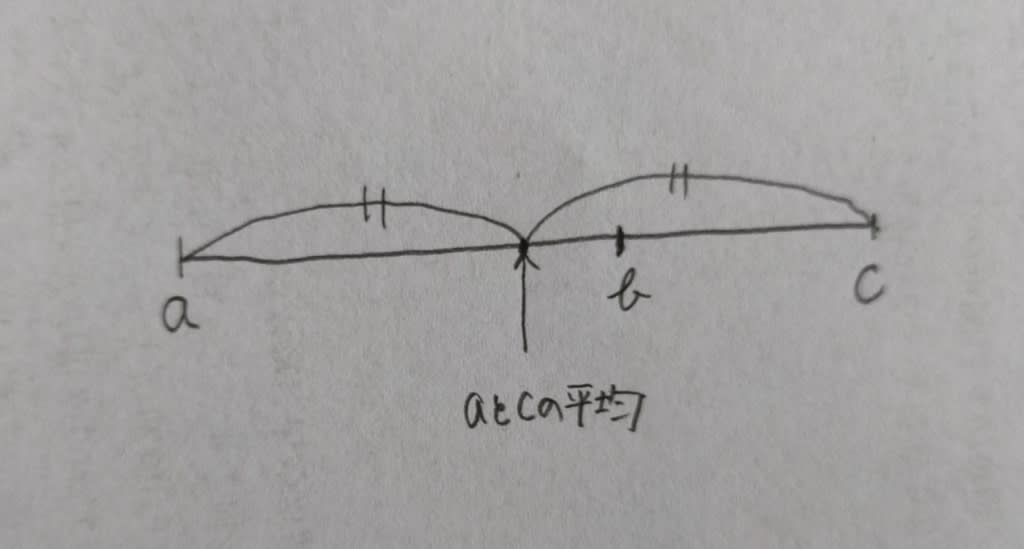　　　　　　　　　　　　　　　　　　　　　　　　　ここに、その他の条件も付け加えて、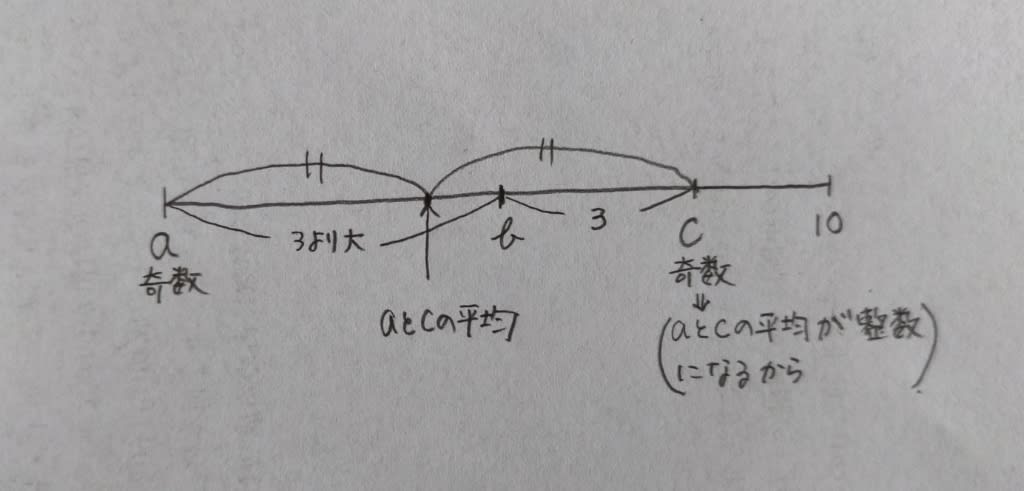
aとbの差は、bとcの差よりも大きいので、3より大きく、4以上です。　　　　　　　　　　　　　　　　　　　　もしもc=9ならば、b=6、aは、6よりも4以上小さいから、1か2。でもaは奇数だからa=1。　　　　　　　　　　　　　　　　　　　　　　　　　　　c=7ならば、b=4。aは4よりも4以上小さいから、なんぼ何でも0で、もう正の整数にはならない。　　　　　　　　　　　　　　　　　　　　　　　　したがって、a=1、b=6、c=9。a+b+c=1+6+9=16。正解は16です。

地方初級の数的推理 5

2021年出題。　　　　　　　　　　　　　　　　　　　　　　　A〜Fは、1〜9の互いに異なる6個の整数である。　　　　　　　　　　　　　　　　　　　　　　　　　　次の3つの関係式が成り立つとき、AとDの差はいくらか。　　　　　　　　　　　　　　　　　A✕B✕C＝252　　　　　　　　　　　　　　　　　　　B✕D✕E＝108　　　　　　　　　　　　　　　　　　C✕E✕F＝70（選択肢省略）　　　　　　　　　　　　　1〜9を使う積の計算パズルです。　　　　　　　　　　　　この場合は、「5」と「7」を探しにいくのが定跡です。　　　　　　　　　　　　　　　　　　　　1〜9の中には、2の倍数が4つ含まれていますし、3の倍数が3つ、4の倍数が2つ含まれています。　　　　　　　　　　　　　　　　　　　　　　　でも、5の倍数は「5」のみ、7の倍数は「7」のみです。　　　　　　　　　　　　　　　　　　　　だから、いくつかの数を掛け合わせたときに5で割り切れる数になれば、掛け合わせた数の中に、必ず5が含まれていることが分かるのです。　　　　　　　　　　　　　　　　　　　　掛け合わせたときに、それが7で割り切れる数になったときも同様です。　　　　　　　　　　　　　　　ただし、1〜10の場合は、たとえ掛け合わせた数が5で割り切れたとしても、掛け合わせた数の中に必ず「5」が含まれているとは限りませんね。　　　　　　　　　　　　　　　　　　　この場合は、掛け合わせた数の中に「5」か「10」が含まれていたとして考えていきます。　　　　　　　　　　　　　　　　　　　　　　　　とりあえず、素因数分解します。
①式より、A、B、Cの中に「7」がいることが分かります。　　　　　　　　　　　　　　　　　　　　　　　また、③式より、C、E、Fの中にも「7」がいることが分かります。　　　　　　　　　　　　　　　　もちろん、A、B、C、E、Fの中に7は1つしかないのだから、Cが「7」です。　　　　　　　　　　次に、「5」を見つけましょう。　　　　　　　　　　　　①式にも②式にも「5」はいません。　　　　　　　　　　　　　③式に「5」がいます。　　　　　　　　　　　　　　　　Cは「7」だったので、EかFが「5」です。　　　　　　　　　　　　　　　　　　　　　　　でも、Eが「5」だったとすると、②式の掛け算の結果が5で割り切れる数になっていないとおかしい。　　　　　　　　　　　　　　　　　　よって、Fが「5」。　　　　　　　　　　　　　　　　まるで、「7」がお父さん、「5」がお母さんで、どこに自分の父や母がいるのかを探しているようですね。　　　　　　　　　　　　　　　　ここまでくれば、あとは適当にやれば正解にたどりつけます。


結論は、
AとDの差は6−4＝2。　　　　　　　　　　　　　　　　　正解は、2です。

地方初級の数的推理 4

2021年出題。　　　　　　　　　　　　　　　　　　　　　1円玉が2枚、5円玉が4枚、10円玉が2枚の計8枚の硬貨がある。　　　　　　　　　　　　　　この中から、5枚を選んだとき、選んだ硬貨の合計金額が、残った硬貨の合計金額より大きくなる場合は何通りあるか。　　　　　　　　　　　　　　　なお、同じ金額の硬貨は区別しないものとする。（選択肢省略）　　　　　　　　　　　　　　　　　　　こういうことですね。
どれを選んだか?ということになれば、選んだ5枚の組み合わせを探すことになります。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　しかし、どれを選ばなかったか?ということになれば、選ばなかった3枚を探すことになりますね。　　　　　　　　　　　　　　　　　　　　　　こりゃあ、選ばなかった3枚の硬貨を探す方が楽ちん〜。　　　　　　　　　　　　　　　　　　　　　　　　8枚の硬貨の合計金額は、1×2＋5×4＋10×2＝42円。　　　　　　　　　　　　　　　　　　　　　　　　これの半分は21円ですから、選ばなかった硬貨の合計金額は210円未満、選んだ硬貨の合計金額は210円超。


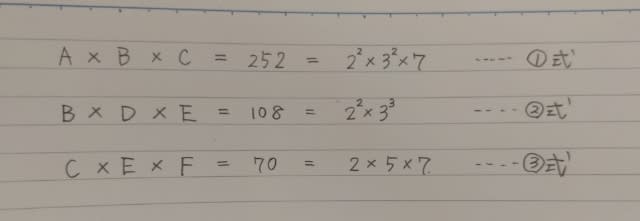
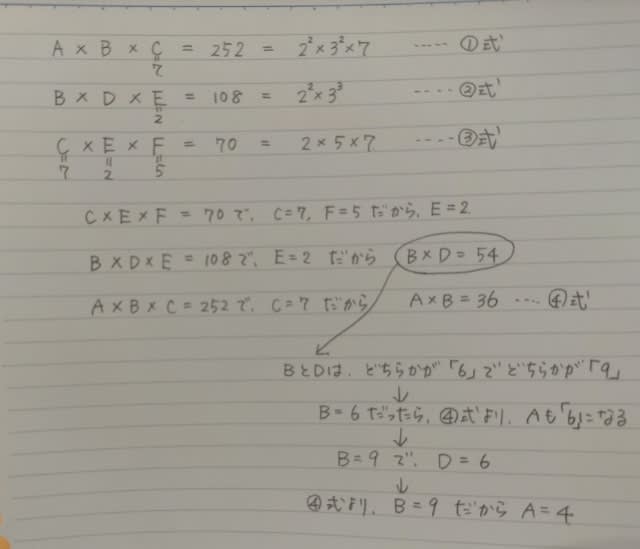
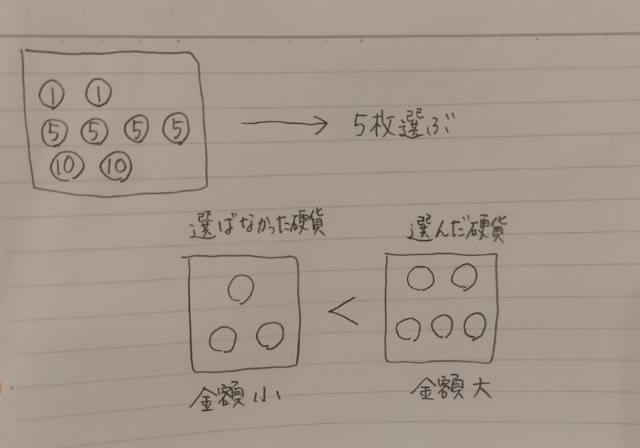
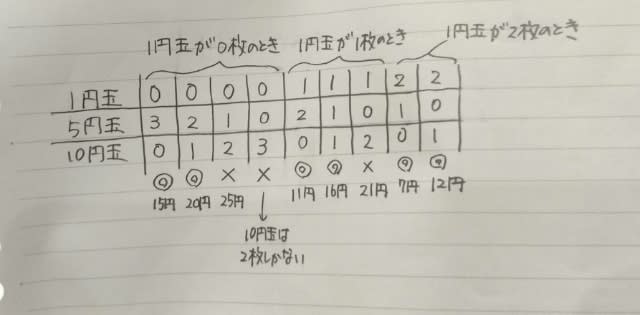3枚で210円未満になる組み合わせを探します。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　◎印のものが条件を満たす組み合わせです。　　　　　　　　　　　　　　　　　　　　　　　　繰り返しますが、選ばなかった3枚の硬貨が決まれば、自動的に選んだ5枚の硬貨も決まりますね。　　　　　　　　　　　　　　　　　　　以上より、正解は6通りであります。

地方初級の数的推理 3

2021年出題。　　　　　　　　　　　　　　　　　　　　　濃度11%の食塩水の入った容器に水を150g追加したところ、食塩水の濃度が5%になった。　　　　　　　　　　　　　　　　　　　　この容器に最初から入っていた食塩水は何gか。（選択肢省略）　　　　　　　　　　　　　　　　　食塩水の問題では、水＝0%、食塩＝100%です。　　　　　　　　　　　　　　　　　　　　　　　この容器に最初から入っていた食塩水の量をx（g）として、図にすると、
実は、上下を掛け合わせた方程式を解けば終わりです。
正解は、125gです。

地方初級の数的推理 2

2021年出題。　　　　　　　　　　　　　　　　　　高校3年生の理科の選択科目のうち、物理選択者は90人、生物選択者は116人である。　　　　　　　　　　　　　　　　　　　　　　　　　男女別では、生物を選択している男子は物理を選択している男子の1.2倍、生物を選択している女子は物理を選択している女子の1.4倍であった。　　　　　　　　　　　　　　　　　　このとき、物理を選択している男女の差は何人か。（選択肢省略）　　　　　　　　　　　　　　　　こんな表に整理します。
物理を選択している男子をx人、物理を選択している女子をy人として、ここに条件を記入すると、
この表から、x＋y＝90、1.2x＋1.4y＝116という連立方程式ができます。（2.2x＋2.4y＝206でも構いません）　　　　　　　　この連立方程式を解きます。
よって、物理を選択している男女の差は50−40＝10人。　　　　　　　　　　　　　　　　　　　正解は10人です。