2021年出題。 次の図は、わが国の第21回から第25回までの参議院議員通常選挙における年代別投票率の推移を示したものであり、表は第24回及び第25回参議院議員通常選挙における18歳と19歳の投票率を示したものである。 ただし、ここでいう投票率とは、全国の投票区から回ごとに定められた数の投票区を抽出して行われた調査による数値である。 あとのア〜エのうち、この図からいえることとして正しいものを◯、誤っているものを✕とした場合、正しい組合せはどれか。1〜5から一つ選べ。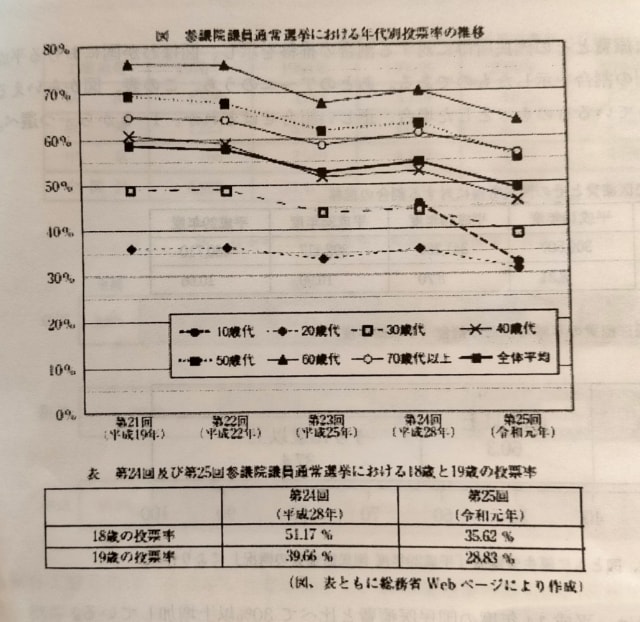
ア 第21回から第23回までの参議院議員通常選挙における20歳代、30歳代、40歳代、50歳代及び60歳代の投票率は、年代が高いほど高くなっている。 イ 第24回及び第25回参議院議員通常選挙のいずれにおいても、10歳代、20歳代、30歳代、及び40歳代の投票率は全体平均よりも低い。 ウ 第24回参議院議員通常選挙における10歳代の投票率は50%に満たないが、その回の18歳の投票率は50%を超えており、同回の19歳の投票率より15ポイント以上高い。 エ 各年代の第24回参議院議員通常選挙における投票率と第25回参議院議員通常選挙における投票率とを比べると、その差が10ポイント以上であるのは10歳代のみであり、18歳と19歳それぞれの第24回参議院議員通常選挙における投票率と第25回参議院議員通常選挙における投票率の差も10ポイント以上ある。
肝心の資料の画像がボヤケて分かりにくいので、赤で補足しました。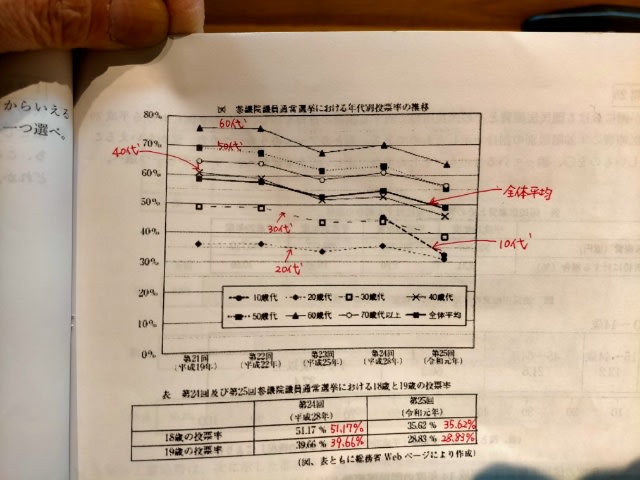
ア‥‥‥21回から23回に限らず、全ての回に当てはまっています。(10歳代、70歳代以上はアでは触れていません)もちろん◯。
イ‥‥‥これも全くその通り。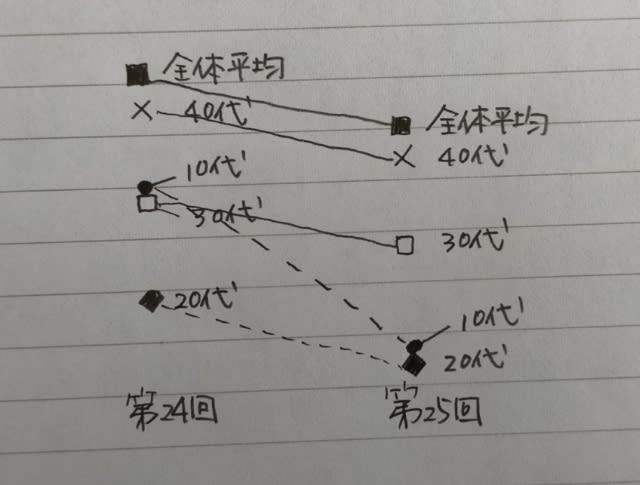
ウ‥‥‥第24回は、10歳代の投票率が45%、その回の18歳の投票率が51.17%なので、ここまでは正しい。 でも、19歳の投票率が39.66%なので、その差は51.17−39.66=11.51ポイント。ウは✕。 エ‥‥‥10代は45%→33%、20代は36%→31%、30代は44%→39%、40代は53%→46%、50代は63%→55%、60代は70%→64%、70以上は61%→57%なので、確かに10ポイント以上差があるのは10代のみ。 そして18歳は51.17%→35.62%、19歳は39.66%→28.83%なので、どちらも10ポイント以上の差があり、後半も正しい。 よって、エは◯。 正解は、肢3です。


ア 第21回から第23回までの参議院議員通常選挙における20歳代、30歳代、40歳代、50歳代及び60歳代の投票率は、年代が高いほど高くなっている。 イ 第24回及び第25回参議院議員通常選挙のいずれにおいても、10歳代、20歳代、30歳代、及び40歳代の投票率は全体平均よりも低い。 ウ 第24回参議院議員通常選挙における10歳代の投票率は50%に満たないが、その回の18歳の投票率は50%を超えており、同回の19歳の投票率より15ポイント以上高い。 エ 各年代の第24回参議院議員通常選挙における投票率と第25回参議院議員通常選挙における投票率とを比べると、その差が10ポイント以上であるのは10歳代のみであり、18歳と19歳それぞれの第24回参議院議員通常選挙における投票率と第25回参議院議員通常選挙における投票率の差も10ポイント以上ある。

肝心の資料の画像がボヤケて分かりにくいので、赤で補足しました。

ア‥‥‥21回から23回に限らず、全ての回に当てはまっています。(10歳代、70歳代以上はアでは触れていません)もちろん◯。

イ‥‥‥これも全くその通り。

ウ‥‥‥第24回は、10歳代の投票率が45%、その回の18歳の投票率が51.17%なので、ここまでは正しい。 でも、19歳の投票率が39.66%なので、その差は51.17−39.66=11.51ポイント。ウは✕。 エ‥‥‥10代は45%→33%、20代は36%→31%、30代は44%→39%、40代は53%→46%、50代は63%→55%、60代は70%→64%、70以上は61%→57%なので、確かに10ポイント以上差があるのは10代のみ。 そして18歳は51.17%→35.62%、19歳は39.66%→28.83%なので、どちらも10ポイント以上の差があり、後半も正しい。 よって、エは◯。 正解は、肢3です。












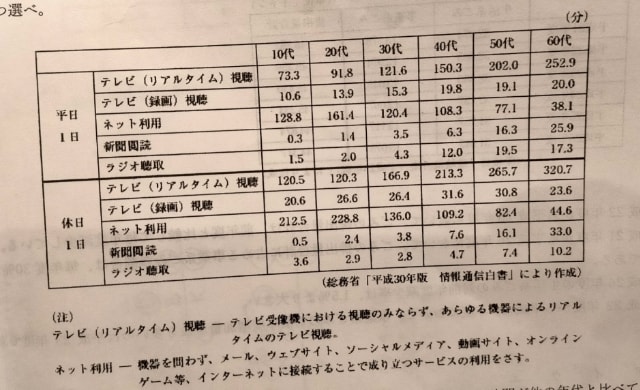




 イは◯ ウ‥‥‥これもイと同じく、増加率の比較です。 イと同じようにしてもかまいませんが、この場合、もっと簡単な方法がありますよ。 2013年から2020年にかけて、ハイブリッド車は、ざっと見て3倍になっています(2850→9281)。 それに対して、電気自動車は5倍(24→117)ですので、電気自動車の増加率のほうが大きい。ウは✖。(この時点で正解は3) このように、増加率の比較をするときに、何倍になったかという視点も重要です。 エ‥‥‥またまた増加率。 2019年の増加率は14/91。 2020年の増加率は12/105。 分母が大きくなり、分子が小さくなっているので、増加率は小さくなっています。(アについても、同じことがいえます)よって✖。 正解は
イは◯ ウ‥‥‥これもイと同じく、増加率の比較です。 イと同じようにしてもかまいませんが、この場合、もっと簡単な方法がありますよ。 2013年から2020年にかけて、ハイブリッド車は、ざっと見て3倍になっています(2850→9281)。 それに対して、電気自動車は5倍(24→117)ですので、電気自動車の増加率のほうが大きい。ウは✖。(この時点で正解は3) このように、増加率の比較をするときに、何倍になったかという視点も重要です。 エ‥‥‥またまた増加率。 2019年の増加率は14/91。 2020年の増加率は12/105。 分母が大きくなり、分子が小さくなっているので、増加率は小さくなっています。(アについても、同じことがいえます)よって✖。 正解は