2019年度大阪府、豊能地区、大阪市、堺市教員採用試験小学全科4

多角形について述べた次の各文のうち、常に正しいものはどれか。1～5から一つ選べ。　　　　　　　　　　　　　　　　　　　①3つの内角のうち、その2つの大きさが26º、58ºの三角形は、鋭角三角形である。　　　　　　　　　　　　　　　　　　　②1つの内角の大きさが60ºである平行四辺形の4つの外角の和は、1080ºである。　　　　　　　　　　　　　　　　　　　③五角形で、4つの内角の和が410ºのとき、残りの内角の大きさは、120ºである。　　　　　　　　　　　　　　　　　　　④6つの辺の長さがすべて等しい六角形は正六角形である。　　　　　　　　　　　　　　　　　　　⑤正十角形では、1つの外角の大きさは、1つの内角の大きさの1/4である。　　　　　　　　　　　　　　　　　　　①三角形の内角の和は180ºですから、そのうちの2つが26ºと58ºなら、もう一つの内角は、180－（26＋58）＝96ºです。これは鈍角（90ºより大きい角）なので、鈍角三角形です。　　　　　　　　　　　　　　　　　　　②何角形であろうが、外角の和は、360ºです。実際に調べてみても、やはり360ºですね。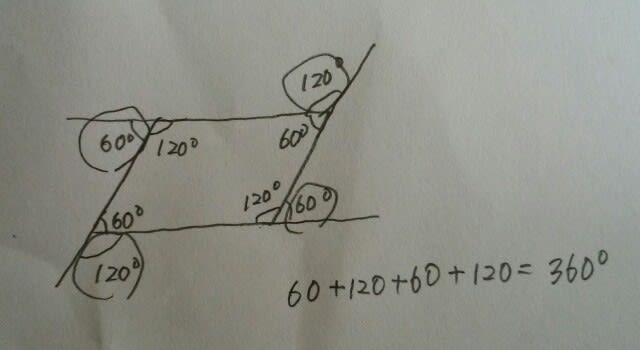　　　　　　　　　　　　　　　　　　　　③n角形の内角の和は、180（n－2）ですから、五角形の内角の和は、180×（5－2）＝180×3＝540ºです。そのうちの4つの内角の和が410ºなので、もう一つの内角は、540－410＝130ºです。　　　　　　　　　　　　　　　　　　　　　　　④正多角形とは、全ての辺の長さと全ての内角の大きさが等しい多角形です。6つの辺の長さが等しいだけでは、まだ正六角形かどうかは分かりません。例えば、　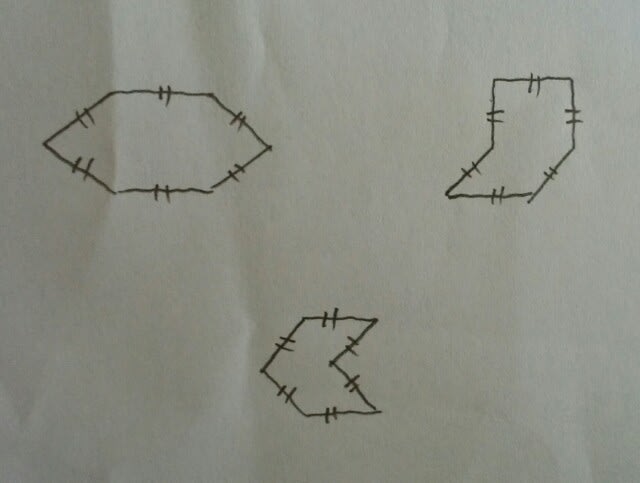　　　　　　　　　　　　　　　　　　　　　　　⑤　②でも述べたように、何角形でも、外角の和は360ºです。正十角形には、当然ながら、10個の内角と10個の外角があります。そして、正十角形ですから、全ての内角どうし、全ての外角どうしは同じ角度です。なので、1つの外角は360÷10＝36ºで、1つの内角は、次の図より、180－36＝144ºです。144÷36＝4ですから、確かに1/4になっています。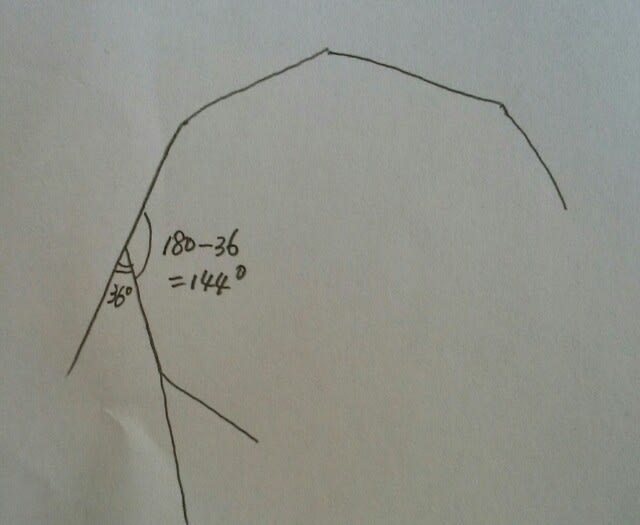正解は、肢⑤です。ここをポチッとお願いします。→
にほんブログ村

2018年度国家一般職（大卒）1

2種類の球種（直球、変化球）のいずれかを、それぞれ1/2の確率でランダムに投げ分ける機械を相手に、Aがバッティングを行う。Aがバットにボールを当てる確率は表のとおりであり、いま投じられている球種と、その直前に投じられた球種によって決まっている。また、同じ球種が3球以上続けて投じられた場合の3球目以降をAがバットに当てる確率は、この表の確率に1/6を加えた値になるものとする。　　　　　　　　　　　　　　　　　　いま、この機械が1球目に直球を投じた後、直球又は変化球をランダムに3球投じたとき、Aが、2球目以降に投じられた3球全てをバットに当てる確率はいくらか。そりゃあ、直球ばかり続けたり、変化球ばかり続ければ、バッターも目が慣れてくるので、バットに当てる確率は上がります。しかし、直球を続けて3球見せられて、次に変化球がくれば、この表の1/3より、確率は少し下がるのではないでしょうか？本問は、「そんなことまで考えなくてよろしい。」ということで……。ついつい、野球の話になると、要らないことまで考えてしまいます。こんな表を作ります。例えば、この機械が、2球目以降、○→○→○と投げる確率は1/8です。この時（○→○→○ときたとき）に、Aが全てバットに当てる確率は、ここで、勘のいい人（又は去年も受けた人）は、「これは計算大会のつもりやな。去年の反復試行もそやったで」と気がつくと思います。つまり、これを後7回繰り返して、その和を求めればいいのです。計算をしくじると一巻の終わり。全てに1/8がくっつきますから、まとめて最後に1/8を掛けることにします。こうなります。正解は、肢2です。ここをポチッとお願いします。→
にほんブログ村

2019年度大阪府、豊能地区、大阪市、堺市教員採用試験小学全科3

下の図において、直線lはy＝2/3x＋4のグラフである。点Pはl上の点であり、Pのx座標は正である。Pからx軸にひいた垂線がx軸と交わる点をQとする。PQ：OQ＝2：1となるとき、線分OPの長さはいくらか。1～5から一つ選べ。点Pのx座標をtとすると、PQ：OQ＝2：1だから、次のようになります。この点Pは、直線l上にあるので、点Pの座標を直線lの式に代入します。よって、OPの長さは、三平方の定理より、3√5です。正解は、肢5です。ここをポチッとお願いします。→
にほんブログ村

2019年度大阪府、豊能地区、大阪市、堺市教員採用試験小学全科2

下の図のように、碁石を正三角形状に並べる。1辺の個数が、4個、5個、6個のとき、並べる碁石の個数はそれぞれ9個、12個、15個である。碁石の個数が135個のとき、1辺の個数は何個になるか。1～5から一つ選べ。こういう問題は、ほとんど2つの解法があります。すなわち、①数列の問題として考える。②方程式の問題として考える。まず、①として考えてみると、1辺の個数と、並べる碁石の総数を対応させた表を作ってみます。総数は、3ずつ増加する等差数列です。だから、正解は、肢4です。等差数列の公式を使って、面倒なことをしましたが、別にこれでも構いません。実は、等差数列の場合、上の数に公差を掛けて、それに何かを足すか引くかをすれば、必ず下の数になるという性質があるのです。②で考えてみると、これが一番シンプルで分かり安いですねぇ。ここをポチッとお願いします。→
にほんブログ村

2019年度大阪府、豊能地区、大阪市、堺市教員採用試験小学全科1

9x2乗－6x＋1は、なんだか因数分解できそうですね。ってか、すぐできる。もしも、3x－1がいくらかが分かれば、それを2乗したものが正解です。3x－1がいくらは分かるのでしょうか？ってか、すぐに分かります。よって、求める値は、√5を2乗した5です。正解は、肢3です。ここをポチッとお願いします。→
にほんブログ村