国家一般職（高卒）の数的推理 2

2021年出題。　　　　　　　　　　　　　　　　　　　図のような縦12cm、横21cmの長方形ABCDがあり、辺ABの中点をEとし、辺CDの中点をFとする。　　　　　　　　　　　　　　　　　　点Pは線分FE上を点Fの位置から毎秒1cmの速度で、点Qは辺BC上を点Bの位置から毎秒2cmの速度で同時に移動する。　　　　　　　　　　　　　このとき、三角形APQの面積が、最初に長方形ABCDの面積の7分の1になるのは、点P及び点Qが移動を始めてから何秒後か。（選択肢省略）
長方形の面積の7分の1は、21×12÷7=36なので、三角形APQの面積が初めて36になるときを求めます。　　　　　　　　　　　　　　　　　　普通に、x秒後に三角形APQの面積が36になるとして、方程式をつくりましょう。　　　　　　　　　　　　　　　　　　　　　　　　　図は、こんな感じですね。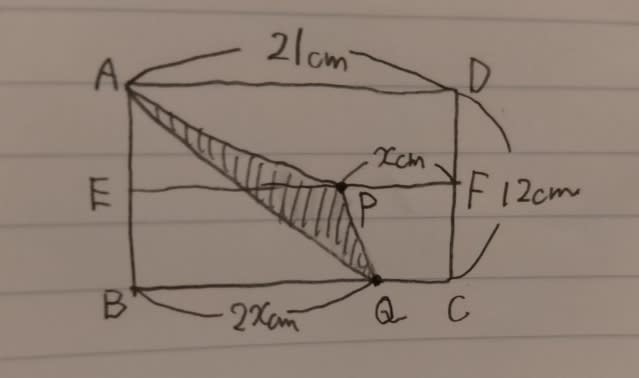
もちろん、斜線部の三角形の面積は、長方形ABCD−三角形ABQ−台形PQCF−台形APFDとなるところですが、そういう方程式にすると、かなり式が難しくなります。　　　　　　　　　　　　　　　　　　　　　　　　　そこで、工夫をします。　　　　　　　　　　　　　　　　三角形APQの辺AQと線分EFの交点をRとして、三角形APQを、三角形ARPと三角形QRPに分割します。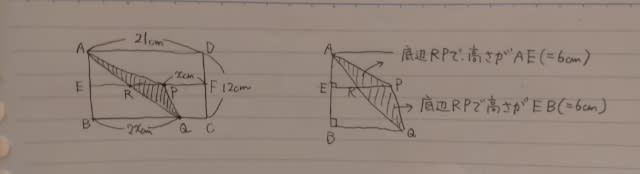
RPの長さはxを使ってどう表されるでしょうか?　　　　　　　　　　　　　　　　　　　　　　　　　中点連結定理②より、ER=xだから、RP=21−2x。




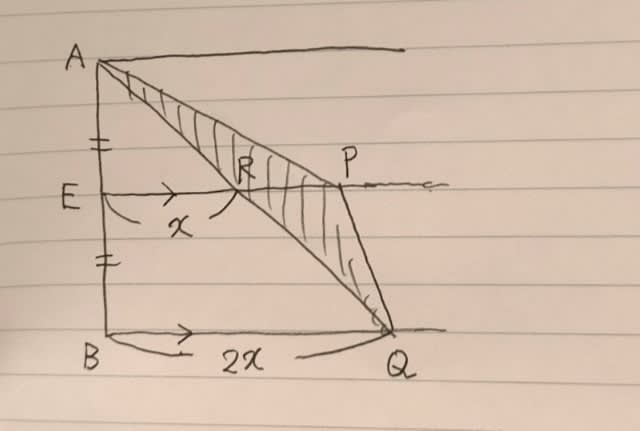
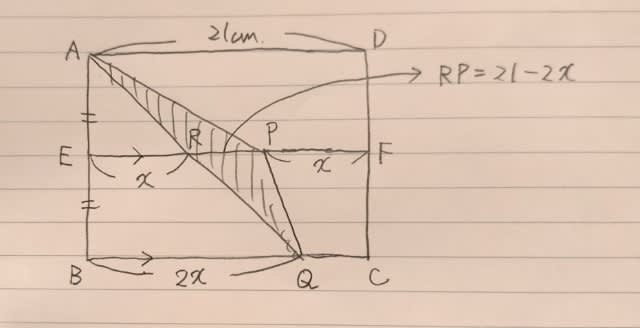
また、三角形ARPも、三角形QRPも、底辺がRPで、高さが6cmなのだから、同じ面積。　　　　　　　　　　　　　　　　　　　　　　　三角形APQ=2×三角形ARPです。　　　　　　　　　　　よって、
正解は、7.5秒後です。

国家一般職（高卒）の数的推理 1

2021年出題。　　　　　　　　　　　　　　　　　　　A、B、Cは、3人合わせて345万円の所持金を持っている。　　　　　　　　　　　　　　　　　　　Aは12%、Bは10%、Cは8%の年利率で全所持金を銀行へ預けたところ、1年後に、Aの利息とBの利息とCの利息の比は、3:2:1となった。　　　　　　　　　　　　　　　　　　　　　このとき、A、B、Cが受け取った利息の合計はいくらか。　　　　　　　　　　　　　　　　　　ただし、利息に係る税金は無視するものとする。（選択肢省略）　　　　　　　　　　　　　　　　　A、B、Cの所持金を、それぞれa万円、b万円、c万円とすると、こうなりますね。A、B、Cが受け取った利息の比は、0.12a:0.1b:0.08cですが、これをできるだけ簡単にしましょう。

これが3:2:1なので、6a:5b:4c=3:2:1。　　　　　　　　　　　　　　　　　　　　　　これは、6aは4cの3倍、5bは4cの2倍だという意味ですね。

つまり、
3人の所持金の合計は345万円だから、
これで3人の所持金が分かりました。

利息の合計は、
正解は、36万円です。　　　　　　　　　　　　　　　　　（補足）a:b=c:dのとき、a×d=b×cとなることは、よく知られていますが、a:b:c=d:e:fのときはどうなるのでしょうか？　　　　　　　　　　　　　　　　　　　　　　　　これは、覚える必要はないと思いますが、こうなります。　　　　　　　　　　　　　　　　　　　　a×e×f=b×d×f=c×d×e。　　　　　　　　　　　　　　ちょっとこれを使ってみましょうか。　　　　　　　　　　所持金の比が6a:5b:4cだったところから先をやってみますと、