図Ⅰのように、目盛りの付いた直方体型の水槽があり、その中に蓋のない2種類の円柱容器ア、イが固定されている。 水槽の高さは40cm、水槽の底面積は1000平方センチメートル、アの高さは20cm、イの高さは30cmである。 この水槽に、蛇口から毎分1000立方センチメートルの水を入れ、水槽の水面の高さを目盛りで読み取ったところ、図Ⅱのように点A〜Dで傾きが変わるグラフになった。 グラフにおいて、水の入れ始めから点Aまでの時間は12分、点Bから点Cまでの時間は9分であった。 このとき円柱容器アとイの底面積の差は何平方センチメートルか。 ただし、水槽と円柱容器の厚さは無視するものとする。また、円柱容器には蓋がないため、円柱容器の高さまで水面がくると、その中に水が入っていく。
ポイントは、一つだけです。次のことを考えて下さい。
底面積×高さ＝体積(容積)ですから、この場合、底面積＝900÷30＝30平方センチメートル。 そう、底面積を知りたけりゃ、入っている水の量を、高さで割ればいいのです。 さて、問題文を見ますと、蛇口から毎分1000立方センチメートルの水を入れたと書いてあります。 点Aまで、12分水を入れたのだから、12000立方センチメートルの水を入れたのです。 その時の水面の高さは20cm。ゆえに、このときの底面積は12000÷20＝600平方センチメートルです。 よって、アの底面積+イの底面積＝400平方センチメートルです。
点Aから点Bまでが平らになっているのは、その間、蓋のない容器アの中に水が入っていくからですね。 容器アが満水になったのが点B。その後9分水を入れたので、9000立方センチメートルの水が投入され、高さは10㎝上昇。 この時の底面積は、9000÷10＝900平方センチメートル。 だから容器イの底面積は100平方センチメートルです。
ということは、容器アの底面積は400-100＝300平方センチメートルです。 よって、AとBの底面積の差は300-100＝200平方センチメートルで、正解は、肢3です。 ここをポチッとお願いします。→
ポイントは、一つだけです。次のことを考えて下さい。
底面積×高さ＝体積(容積)ですから、この場合、底面積＝900÷30＝30平方センチメートル。 そう、底面積を知りたけりゃ、入っている水の量を、高さで割ればいいのです。 さて、問題文を見ますと、蛇口から毎分1000立方センチメートルの水を入れたと書いてあります。 点Aまで、12分水を入れたのだから、12000立方センチメートルの水を入れたのです。 その時の水面の高さは20cm。ゆえに、このときの底面積は12000÷20＝600平方センチメートルです。 よって、アの底面積+イの底面積＝400平方センチメートルです。
点Aから点Bまでが平らになっているのは、その間、蓋のない容器アの中に水が入っていくからですね。 容器アが満水になったのが点B。その後9分水を入れたので、9000立方センチメートルの水が投入され、高さは10㎝上昇。 この時の底面積は、9000÷10＝900平方センチメートル。 だから容器イの底面積は100平方センチメートルです。
ということは、容器アの底面積は400-100＝300平方センチメートルです。 よって、AとBの底面積の差は300-100＝200平方センチメートルで、正解は、肢3です。 ここをポチッとお願いします。→
にほんブログ村
下の図について、AB∥CD、EF∥AB、AB＝10cm、EF＝15cmのとき、CDの長さはどれか、①～⑤から一つ選んで番号で答えなさい。
相似な三角形を見つけていきます。まず、
次に、
正解は、肢④です。また、こういう公式を知っておくと、とても便利ですよ。
本問の場合は、
たったこれだけで終わりですからね。😙それでは、練習問題です。これは、2016.7.23の山形県です。
正解は、24cmです。ここをポチッとお願いします。
図のように線分OA、OBを直径とする2つの半円が重ねて置かれている。OA＝OB＝20㎝、∠AOB＝90ºのとき、図の斜線部分の面積として正しいものを、次のア～エから1つ選びなさい。ただし、必要ならば円周率を3.14として計算しなさい。
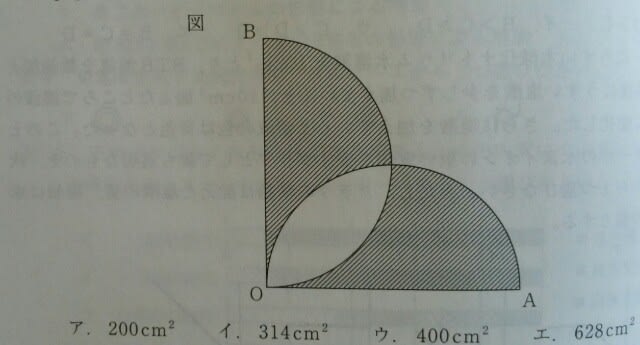今日は、一発で終わってしまいます。
正解は、肢アです。ある駅に、こんな自販機ありました。
－2ºC冷えている＝2ºCぬるい。
下の図の三角形の面積として正しいものを1つ選び番号で答えなさい。ただし、単位はすべて㎠である。
三角形の2つの角度が、90ºと15ºなので、もう一つの角度は75ºです。75ºが2つあれば、150ºになります。150ºの外角は30ºです。よって、1：2：√3の比を知っていれば、中学の範囲で解くことができます。
まず、△EBDの面積は、 （2√3＋4）×2÷2＝2√3＋4。 T（△EBA）の面積は、2√3×2÷2＝2√3。 よって、2S＝2√3＋4－2√3＝4。ゆえに、S＝2。正解は、肢③です。 また、どうしても分からなかったら、選択肢を使いましょう。√2は、約1.4。√3は、約1.73だから、√6は、√2×√3＝約1.4×約1.73＝約2.422＝約2.4。肢①は1、肢②は約2.4－約1.4＝約1。肢3は2、肢④は2×約1.73＝約3.46、肢⑤は約2.4＋約1.4＝約3.8です。
と、見た目でやってもいいですし、もう少し厳密に、
とやってもいいですね。肢①と肢②の値が近接していますので、もしも正解が1㎠前後だつたとしたら、正解が分からなかったでしょう。
四角形ADEFは、円に内接しています。円に内接する四角形は、向かい合う角の和が180º（円に内接する四角形の定理）だから、とりあえず、∠DAF＝70º。これで、肢①か⑤の二択になります。次に、AB＝BC＝CDより、△ABOと△BCOと△CDOは合同。
ゆえに∠COD＝40º。正解は、肢⑤です。△AODにおいて、∠AOD＝120ºで、OA＝ODだから、
∠DAF＝70ºだったので、∠OAF＝40º。OA＝OFだから、∠AOF＝180－40×2＝100ºです。
弧ADFに対する中心角は、360－100＝260º。∠AGFは、弧ADFに対する円周角だから、260÷2＝130ºです。（円周角は中心角の半分）
DE＝EFという条件は、関係なかったですね。