2021年出題。 次の図のように、円Oに内接する四角形ABCDがある。 ∠OBC=37°、∠CAD=33°のとき、∠BCDの大きさとして、最も妥当なのはどれか。(選択肢省略)
OA=OB=OC(全て円Oの半径)で、二等辺三角形の底角は等しいので、こうなりますね。
三角形の内角の和は180°なので、△ABCに注目して、a+a+b+b+37+37=180。整理して、a+b=53°。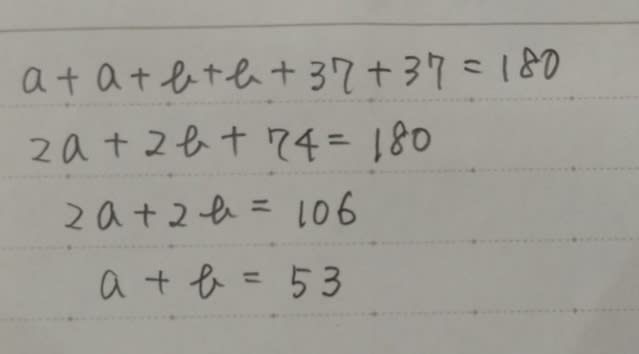 よって、∠BAD=53+33=86°。
よって、∠BAD=53+33=86°。
ここで、円に内接する四角形の定理が登場します。
四角形ABCDは、円Oに内接しているので、∠BAD+∠BCD=180°。 ∠BAD=86°だから、∠BCD=180−86=94°。 正解は94°です。 えっ? じゃあ円に内接する四角形の定理を知ってなきゃこの問題は解けないの?ということになりますが、まあ、知らなくても何とかなりますけど。 やってみますよ。 上の、∠BAD=86°までは同じで、その先。 弧BCDに対する円周角(∠BAD)が86°だから、その中心角(∠BOD)は、その2倍の172°。
よって、弧BADに対する中心角は360−172=188°。
よって、弧BADに対する円周角である∠BCDは、その1/2の94°です。 な、何? 円周角が中心角の1/2ということも知らなかったらどうするのって? それはそれで何とかなるのですが、かなりややこしくなります。 そのときには、三角形の外角の定理が必要だし、補助線も要ります。 三角形の外角の定理も知らなければ、もっとややこしくなり、もう勘弁して下さい! ゆえに、円に内接する四角形の定理をきちんと覚えて置きましょう。











OA=OB=OC(全て円Oの半径)で、二等辺三角形の底角は等しいので、こうなりますね。

三角形の内角の和は180°なので、△ABCに注目して、a+a+b+b+37+37=180。整理して、a+b=53°。
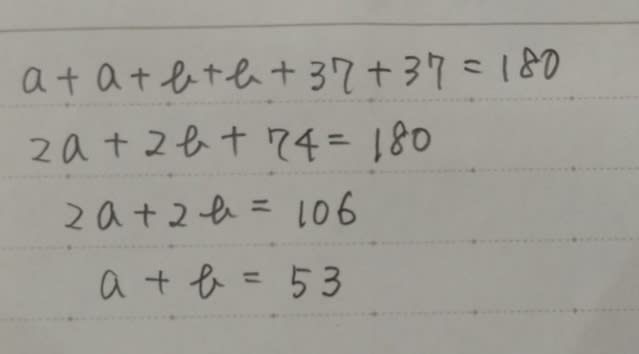 よって、∠BAD=53+33=86°。
よって、∠BAD=53+33=86°。ここで、円に内接する四角形の定理が登場します。

四角形ABCDは、円Oに内接しているので、∠BAD+∠BCD=180°。 ∠BAD=86°だから、∠BCD=180−86=94°。 正解は94°です。 えっ? じゃあ円に内接する四角形の定理を知ってなきゃこの問題は解けないの?ということになりますが、まあ、知らなくても何とかなりますけど。 やってみますよ。 上の、∠BAD=86°までは同じで、その先。 弧BCDに対する円周角(∠BAD)が86°だから、その中心角(∠BOD)は、その2倍の172°。

よって、弧BADに対する中心角は360−172=188°。

よって、弧BADに対する円周角である∠BCDは、その1/2の94°です。 な、何? 円周角が中心角の1/2ということも知らなかったらどうするのって? それはそれで何とかなるのですが、かなりややこしくなります。 そのときには、三角形の外角の定理が必要だし、補助線も要ります。 三角形の外角の定理も知らなければ、もっとややこしくなり、もう勘弁して下さい! ゆえに、円に内接する四角形の定理をきちんと覚えて置きましょう。










































 HADOアイドルウォーズ コスモスCUP 3rdシーズン 2022.9.5 1:07〜約45分 第2試合。
HADOアイドルウォーズ コスモスCUP 3rdシーズン 2022.9.5 1:07〜約45分 第2試合。