ある会社で社員の生活習慣について調査を行った。次のことが分かっているとき、確実にいえるのはどれか。 ○睡眠時間の平均が6時間以上の者は72人であり、6時間未満の者は48人である。 ○朝食を食べる習慣がない者は51人である。 ○朝食を食べる習慣があり、運動する習慣がなく、睡眠時間の平均が6時間未満の者は20人である。 ○朝食を食べる習慣がなく、睡眠時間の平均が6時間未満の者のうち、運動する習慣がある者は、そうでない者より2人多い。 ○運動する習慣がなく、睡眠時間の平均が6時間未満の者は25人である。 ○運動する習慣があり、睡眠時間の平均が6時間以上の者のうち、朝食を食べる習慣がある者は15人であり、そうでない者より5人少ない。 ①運動する習慣がある者は55人である。 ②睡眠時間の平均が6時間以上で、朝食を食べる習慣があり、運動する習慣がない者は15人である。 ③睡眠時間の平均が6時間未満で、朝食を食べる習慣があり、運動する習慣がある者は20人である。 ④睡眠時間の平均が6時間以上の者のうち、朝食を食べる習慣がある者は、そうでない者より少ない。 ⑤朝食を食べる習慣がない者のうち、運動する習慣がある者は、そうでない者より少ない。 キャロル図を使う問題ですね。1〜4番目までの条件を書き込むと、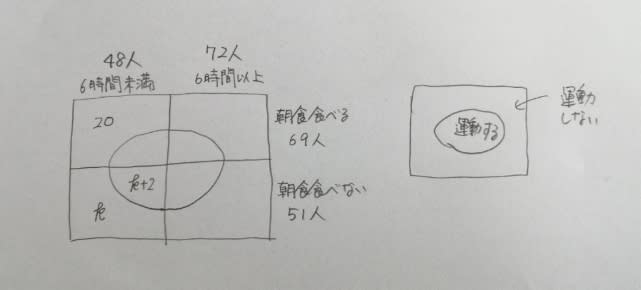
(はじめの条件から、全体で120人。4番目の条件の、そうでない者をk人としています。) ここで、5番目の条件を見ると、ラッキー、ポッキー、k=5だと分かりますので、
睡眠時間が6時間未満の列(左列)の合計は48人だから、
最後の条件を書き込んで、
空いている場所は、引き算すれば人数が分かります。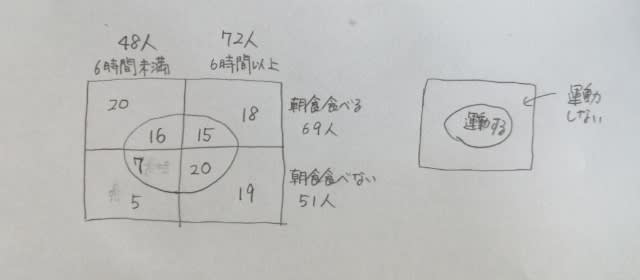
選択肢①58人。②18人。③16人。④確かに少ない。⑤多い。正解は肢④です。 ここをポチッとお願いします。→
にほんブログ村


(はじめの条件から、全体で120人。4番目の条件の、そうでない者をk人としています。) ここで、5番目の条件を見ると、ラッキー、ポッキー、k=5だと分かりますので、

睡眠時間が6時間未満の列(左列)の合計は48人だから、

最後の条件を書き込んで、

空いている場所は、引き算すれば人数が分かります。

選択肢①58人。②18人。③16人。④確かに少ない。⑤多い。正解は肢④です。 ここをポチッとお願いします。→
にほんブログ村












 ここに条件を書き入れまして~。
ここに条件を書き入れまして~。  さて、ここから何が分かるか? 1年生男子が100人で、2年生男子が90人ってことは、結局男子が190人。全員で400人だから、女子は、400-190=210人。その女子のうち90人がフランス語をやってるんだから、残り120人はドイツ語で、k=120です。
さて、ここから何が分かるか? 1年生男子が100人で、2年生男子が90人ってことは、結局男子が190人。全員で400人だから、女子は、400-190=210人。その女子のうち90人がフランス語をやってるんだから、残り120人はドイツ語で、k=120です。 ということは、ドイツ語やってる人は120+120=240人だから、フランス語やってる人は400-240=160人。そのうち90人が女子だから、フランス語やってる男子は160-90=70人。
ということは、ドイツ語やってる人は120+120=240人だから、フランス語やってる人は400-240=160人。そのうち90人が女子だから、フランス語やってる男子は160-90=70人。  正解は、肢③です。 肢①1年生女子は140人です。
正解は、肢③です。 肢①1年生女子は140人です。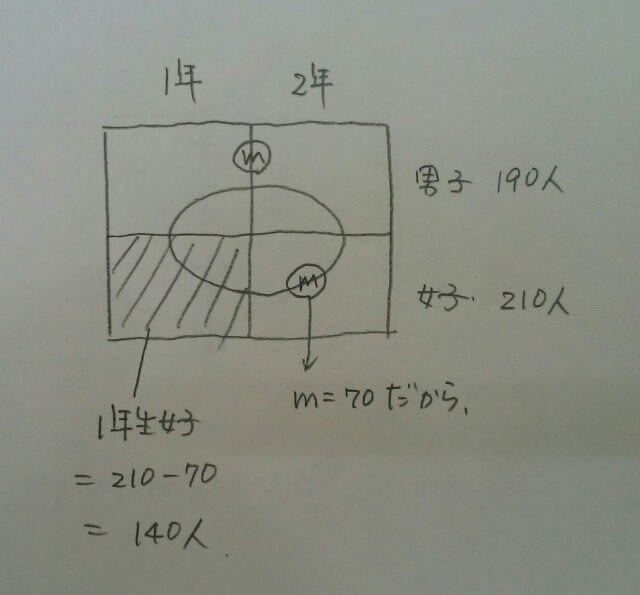 肢②2年生女子は、mとおいたので、m=70より、70人。 肢④ドイツ語男子は、kとおいたので、k=120より、120人。 肢⑤ドイツ語男子とドイツ語女子は同数だから、120人。 ここをポチッとお願いします。→
肢②2年生女子は、mとおいたので、m=70より、70人。 肢④ドイツ語男子は、kとおいたので、k=120より、120人。 肢⑤ドイツ語男子とドイツ語女子は同数だから、120人。 ここをポチッとお願いします。→


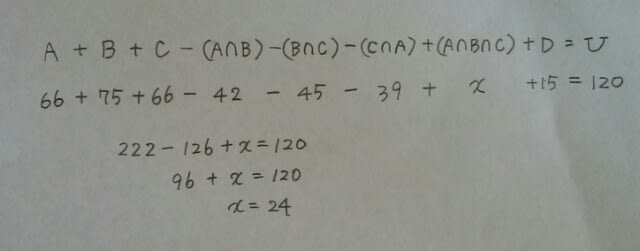 よって、こうなってます。
よって、こうなってます。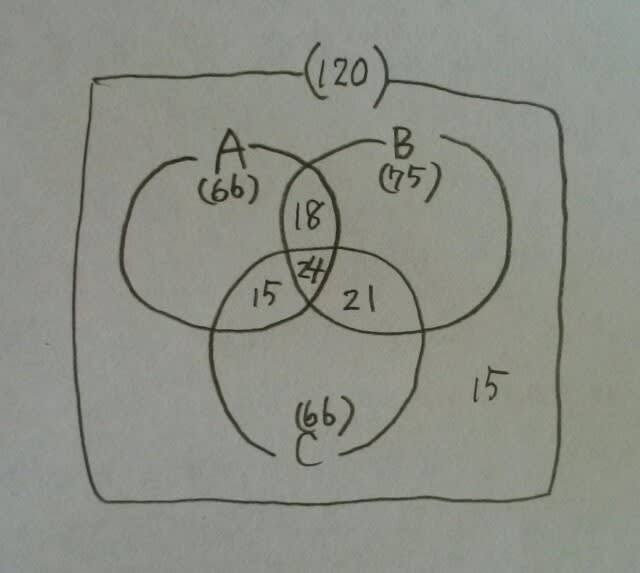 一つも合格していない児童が15人。 二つだけ合格した児童は、18+15+21=54人。 したがって、1曲しか合格できなかった人と3曲とも合格した人の合計は、120-15-54=51人、正解は、肢⑤です。ここをポチッとお願いします。→
一つも合格していない児童が15人。 二つだけ合格した児童は、18+15+21=54人。 したがって、1曲しか合格できなかった人と3曲とも合格した人の合計は、120-15-54=51人、正解は、肢⑤です。ここをポチッとお願いします。→
 仮に、3科目すべてが平均点以上の人が(実際に)10人いたとすると、延べにすると、10×3=30人になってしまい、2科目だけ平均点以上の人が(実際に)30人いたとすると、延べにすると、30×2=60人になります。3科目すべて平均点未満だった者は、何人いたとしても、延べには入りません。ということは、 ♤実際の人数も、延べ人数も分かっている。(本問の場合は、実際250人。延べ342人。)なおかつ、 ♡4つのグループ(3科目が平均点以上、2科目が平均点以上、1科目が平均点以上、0科目が平均点以上)のうち、2つ以上の人数が分かっている(本問の場合は、0科目50人、1科目94人)というときは、ベン図など描くことをせずに、いきなり、
仮に、3科目すべてが平均点以上の人が(実際に)10人いたとすると、延べにすると、10×3=30人になってしまい、2科目だけ平均点以上の人が(実際に)30人いたとすると、延べにすると、30×2=60人になります。3科目すべて平均点未満だった者は、何人いたとしても、延べには入りません。ということは、 ♤実際の人数も、延べ人数も分かっている。(本問の場合は、実際250人。延べ342人。)なおかつ、 ♡4つのグループ(3科目が平均点以上、2科目が平均点以上、1科目が平均点以上、0科目が平均点以上)のうち、2つ以上の人数が分かっている(本問の場合は、0科目50人、1科目94人)というときは、ベン図など描くことをせずに、いきなり、
 正解は、肢②です。ベン図を描かなくてもよいので、助かりますね!ここをポチッとお願いします。→
正解は、肢②です。ベン図を描かなくてもよいので、助かりますね!ここをポチッとお願いします。→ うちは、マンション9階なのですが、玄関前に、かっこいい虫がいました。何という虫か分かりません。
うちは、マンション9階なのですが、玄関前に、かっこいい虫がいました。何という虫か分かりません。