10万円を年利率20%の複利で運用を始めたとき、40万円を超える年数として、最も妥当なのはどれか。ただし、…
 対数、複利計算について知らない人は、前回の記事を見てから戻ってきて下さいね。おっと、前回logについて説明しましたが、一つ説明するのを忘れていました。logの計算の公式をいろいろ紹介しましたが、そもそもlogを使うにあたって、大前提となる事柄があります。それは、
対数、複利計算について知らない人は、前回の記事を見てから戻ってきて下さいね。おっと、前回logについて説明しましたが、一つ説明するのを忘れていました。logの計算の公式をいろいろ紹介しましたが、そもそもlogを使うにあたって、大前提となる事柄があります。それは、 ということです。赤で線を引っ張った条件にあてはまらないときは、計算もできませんし、logを使った議論は成り立ちません。記述式の数学では、この条件を書き忘れて減点ということがよくありますが、公務員試験では、ほとんど気にしなくても構いません。(絶対とは言えませんが)さて、本問について。「年利率」と書いてあるので、利子は1年に1回。x年経つと、利子はx回つきます。前回の、複利計算の公式より、x年後には、
ということです。赤で線を引っ張った条件にあてはまらないときは、計算もできませんし、logを使った議論は成り立ちません。記述式の数学では、この条件を書き忘れて減点ということがよくありますが、公務員試験では、ほとんど気にしなくても構いません。(絶対とは言えませんが)さて、本問について。「年利率」と書いてあるので、利子は1年に1回。x年経つと、利子はx回つきます。前回の、複利計算の公式より、x年後には、
 ここから、はじめて対数をやる人にとっては、信じられないことをします。知ってる人は知ってますよね。そう、「常用対数をとる」のです。
ここから、はじめて対数をやる人にとっては、信じられないことをします。知ってる人は知ってますよね。そう、「常用対数をとる」のです。 よって、正解は肢③です。おいおい、待ってくれって?結構しんどい計算ですね。そこで抜け道。っていうか、むしろこっちの方が本筋かも。
よって、正解は肢③です。おいおい、待ってくれって?結構しんどい計算ですね。そこで抜け道。っていうか、むしろこっちの方が本筋かも。 まあ、資料解釈のつもりで、ひたすら筆算。LECオンラインショップ(E学習センター)
まあ、資料解釈のつもりで、ひたすら筆算。LECオンラインショップ(E学習センター)




 対数、複利計算について知らない人は、前回の記事を見てから戻ってきて下さいね。おっと、前回logについて説明しましたが、一つ説明するのを忘れていました。logの計算の公式をいろいろ紹介しましたが、そもそもlogを使うにあたって、大前提となる事柄があります。それは、
対数、複利計算について知らない人は、前回の記事を見てから戻ってきて下さいね。おっと、前回logについて説明しましたが、一つ説明するのを忘れていました。logの計算の公式をいろいろ紹介しましたが、そもそもlogを使うにあたって、大前提となる事柄があります。それは、 ということです。赤で線を引っ張った条件にあてはまらないときは、計算もできませんし、logを使った議論は成り立ちません。記述式の数学では、この条件を書き忘れて減点ということがよくありますが、公務員試験では、ほとんど気にしなくても構いません。(絶対とは言えませんが)さて、本問について。「年利率」と書いてあるので、利子は1年に1回。x年経つと、利子はx回つきます。前回の、複利計算の公式より、x年後には、
ということです。赤で線を引っ張った条件にあてはまらないときは、計算もできませんし、logを使った議論は成り立ちません。記述式の数学では、この条件を書き忘れて減点ということがよくありますが、公務員試験では、ほとんど気にしなくても構いません。(絶対とは言えませんが)さて、本問について。「年利率」と書いてあるので、利子は1年に1回。x年経つと、利子はx回つきます。前回の、複利計算の公式より、x年後には、
 ここから、はじめて対数をやる人にとっては、信じられないことをします。知ってる人は知ってますよね。そう、「常用対数をとる」のです。
ここから、はじめて対数をやる人にとっては、信じられないことをします。知ってる人は知ってますよね。そう、「常用対数をとる」のです。 よって、正解は肢③です。おいおい、待ってくれって?結構しんどい計算ですね。そこで抜け道。っていうか、むしろこっちの方が本筋かも。
よって、正解は肢③です。おいおい、待ってくれって?結構しんどい計算ですね。そこで抜け道。っていうか、むしろこっちの方が本筋かも。 まあ、資料解釈のつもりで、ひたすら筆算。LECオンラインショップ(E学習センター)
まあ、資料解釈のつもりで、ひたすら筆算。LECオンラインショップ(E学習センター)












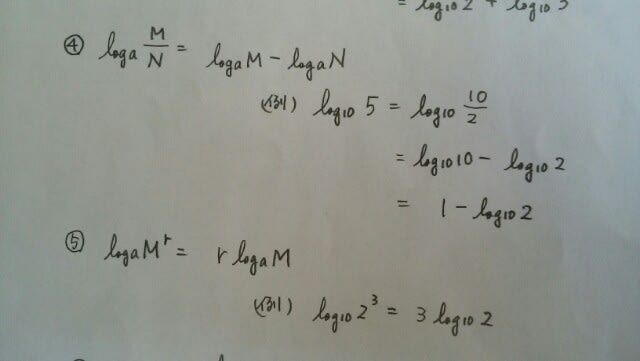
 といったところです。えっ?ややこしい?ちょっと慣れていただきましょう。次の計算をやってみてください。
といったところです。えっ?ややこしい?ちょっと慣れていただきましょう。次の計算をやってみてください。 答えは、
答えは、
 途中の計算過程は、あくまでも一例であって、他にもいろいろあります。最後の数字と一致していれば正解です。もう少し練習したい人は、最後に載せるやつをやって、慣れて下さい。ただ、次回言いますが、根性で何とかすることもできますので、理解するのがどうしても無理なら、ほっといてもいいでしょう。次に、複利計算の公式です。利率A%(複利)で、N回利子がかかると、次のようになります。
途中の計算過程は、あくまでも一例であって、他にもいろいろあります。最後の数字と一致していれば正解です。もう少し練習したい人は、最後に載せるやつをやって、慣れて下さい。ただ、次回言いますが、根性で何とかすることもできますので、理解するのがどうしても無理なら、ほっといてもいいでしょう。次に、複利計算の公式です。利率A%(複利)で、N回利子がかかると、次のようになります。 何?これも難しい?ちょっと練習しましょう。例えば、今200万円を年利率10%の複利で運用を始めたら、3年後はどうなる?
何?これも難しい?ちょっと練習しましょう。例えば、今200万円を年利率10%の複利で運用を始めたら、3年後はどうなる? もう一丁!100万円を、半年複利20%で2年運用すると?
もう一丁!100万円を、半年複利20%で2年運用すると? はい、お疲れさまでした。それでは、対数の計算問題です。
はい、お疲れさまでした。それでは、対数の計算問題です。


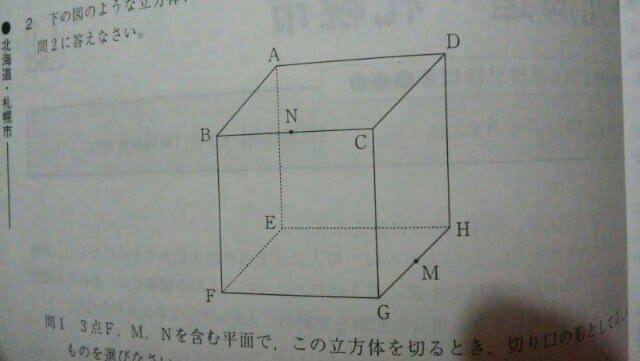 問1 3点F、M、Nを含む平面で、この立方体を切るとき、切り口の形として正しいものを選びなさい。 ア、正三角形 イ、二等辺三角形 ウ、長方形 エ、平行四辺形 オ、台形 問2 頂点Fを出発して立方体の辺の上を動く任意の点Pが、同じ頂点を2度通らず、かつ、点M、Nを通ることなく頂点Dまで移動する場合、行き方は全部で何通りか、正しいものを選びなさい。 ア、3通り イ、4通り ウ、5通り エ、6通り オ、7通り 問1。同じ平面上の2点が出てきたら、その2点をまっすぐ結ぶ。同じ平面上の点ではないときは、絶対に結ばないで下さい。 本問では、FとNは、同じ平面上なので結び、FとMも、同じ平面上なので結びます。MとNは、違う面上にあるので結んではいけません。
問1 3点F、M、Nを含む平面で、この立方体を切るとき、切り口の形として正しいものを選びなさい。 ア、正三角形 イ、二等辺三角形 ウ、長方形 エ、平行四辺形 オ、台形 問2 頂点Fを出発して立方体の辺の上を動く任意の点Pが、同じ頂点を2度通らず、かつ、点M、Nを通ることなく頂点Dまで移動する場合、行き方は全部で何通りか、正しいものを選びなさい。 ア、3通り イ、4通り ウ、5通り エ、6通り オ、7通り 問1。同じ平面上の2点が出てきたら、その2点をまっすぐ結ぶ。同じ平面上の点ではないときは、絶対に結ばないで下さい。 本問では、FとNは、同じ平面上なので結び、FとMも、同じ平面上なので結びます。MとNは、違う面上にあるので結んではいけません。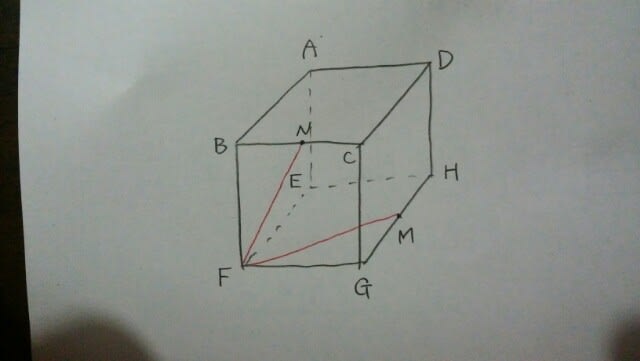 面と面が平行ならば、切り口と切り口も平行です。この立方体が透明な素材でできていると思って、真上から見ると、
面と面が平行ならば、切り口と切り口も平行です。この立方体が透明な素材でできていると思って、真上から見ると、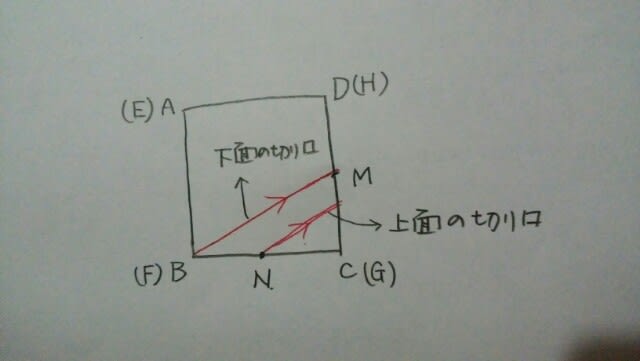 よって、
よって、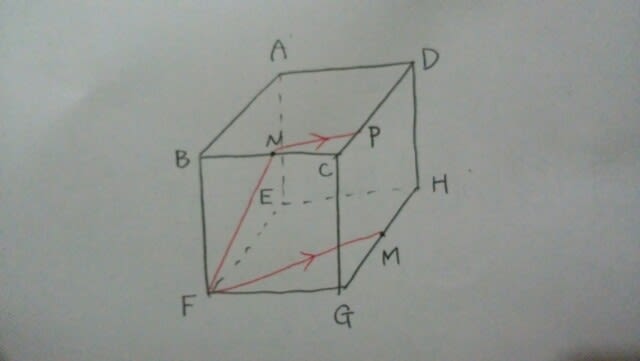 PとMは、同じ平面上なので、まっすぐ結びます。
PとMは、同じ平面上なので、まっすぐ結びます。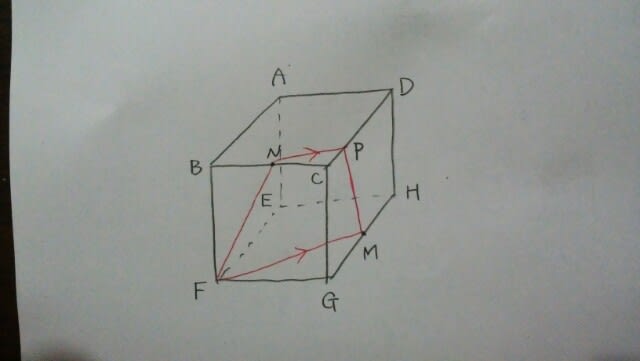 よって、オが正解。 問2 どうせNとMは通れないのだから、辺BCと辺GHは消してしまいましょう。
よって、オが正解。 問2 どうせNとMは通れないのだから、辺BCと辺GHは消してしまいましょう。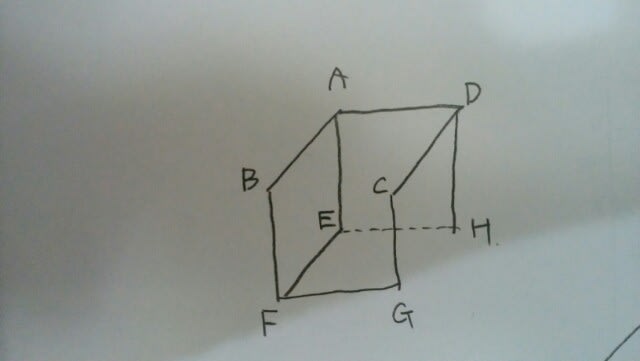 この状態で、同じ頂点を2度通らないようにしてDまで行きます。樹形図をかくといいですね。
この状態で、同じ頂点を2度通らないようにしてDまで行きます。樹形図をかくといいですね。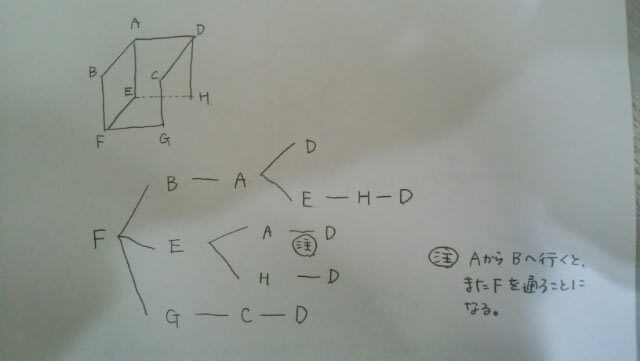 よって、正解はウです。
よって、正解はウです。

 ①全国が約48000で、その10%は4800。中国ブロック合計は2744だから、10%未満。 ②岡山と山口は5.2%の差。約2700の5.2%は、2700×0.052=140.4(百億円)=1兆4040億円。 ③中国ブロックは、四国ブロックの、約2倍です。つまり、中国の半分(50%)が、四国全体に相当します。山口、島根、鳥取を合わせても、50%未満だということは、グラフから明らかです。 ④2744×0.2=548.8(百億円)=5兆4880億円。確かに6兆円未満です。 ⑤全国(約48000)の3%は、48000×0.03=1440。広島は、約2700×0.39=1053。3%未満です。正解は肢④です。
①全国が約48000で、その10%は4800。中国ブロック合計は2744だから、10%未満。 ②岡山と山口は5.2%の差。約2700の5.2%は、2700×0.052=140.4(百億円)=1兆4040億円。 ③中国ブロックは、四国ブロックの、約2倍です。つまり、中国の半分(50%)が、四国全体に相当します。山口、島根、鳥取を合わせても、50%未満だということは、グラフから明らかです。 ④2744×0.2=548.8(百億円)=5兆4880億円。確かに6兆円未満です。 ⑤全国(約48000)の3%は、48000×0.03=1440。広島は、約2700×0.39=1053。3%未満です。正解は肢④です。

 これは、少し危険な問題です。①2006年から、2007年にかけては、名古屋港208→216。千葉港167→169。横浜港138→142。対前年増加率は、
これは、少し危険な問題です。①2006年から、2007年にかけては、名古屋港208→216。千葉港167→169。横浜港138→142。対前年増加率は、 対前年増加率が最も大きいのは名古屋港です。②この数表は、「取扱い量」であって、「取扱い額」は分かりません。単位が百万トンとなっていますね。 ③確かに、2008年から2009年にかけて、横浜港は、かなり減少しています。しかし、名古屋港も同じくかなり減少しています。減少率を調べてみると、
対前年増加率が最も大きいのは名古屋港です。②この数表は、「取扱い量」であって、「取扱い額」は分かりません。単位が百万トンとなっていますね。 ③確かに、2008年から2009年にかけて、横浜港は、かなり減少しています。しかし、名古屋港も同じくかなり減少しています。減少率を調べてみると、 やはり、名古屋港の方が、減少率が大きい。 ④千葉港と横浜港は、いずれの年も千葉港の方が多く、その差は、3300万トン、2900万トン、2700万トン、2300万トン、2900万トン(表の単位が百万トンであることに注意)なので、これは正しい。 ⑤どの年も10%未満であることは明らか。 よって、正解は肢④です。 始めに、少し危険な問題だといったのは、肢②は引っかけなので別にして、肢①と③を検討する前に、肢④を検討しないと、少しロスタイムが生じてしまうということです。④は、引き算で解決できるものなので、こういう肢を優先的にするべきです。 えっ?他の肢は考えなくてもいいの?という声が聞こえてきそうですが、もう一度落ち着いて肢④を眺めて見て下さいよ。他の肢について考える暇があったら、もう一度、引き算を間違えてないか確かめる方が速いのではないでしょうか?
やはり、名古屋港の方が、減少率が大きい。 ④千葉港と横浜港は、いずれの年も千葉港の方が多く、その差は、3300万トン、2900万トン、2700万トン、2300万トン、2900万トン(表の単位が百万トンであることに注意)なので、これは正しい。 ⑤どの年も10%未満であることは明らか。 よって、正解は肢④です。 始めに、少し危険な問題だといったのは、肢②は引っかけなので別にして、肢①と③を検討する前に、肢④を検討しないと、少しロスタイムが生じてしまうということです。④は、引き算で解決できるものなので、こういう肢を優先的にするべきです。 えっ?他の肢は考えなくてもいいの?という声が聞こえてきそうですが、もう一度落ち着いて肢④を眺めて見て下さいよ。他の肢について考える暇があったら、もう一度、引き算を間違えてないか確かめる方が速いのではないでしょうか?