4枚のコインがあり、これを3枚裏返す作業を1回とする。はじめ4枚のコインは全て表に置いてあったとすると、全てのコインを裏にするには少なくとも何回の作業が必要か。 ①3回②4回③5回④6回⑤8回 表を○、裏を×とします。○を1回裏返すと×になり、2回裏返すと○になり、3回裏返すと×になる、というように、あるコインを、奇数回裏返すと×、偶数回裏返すと○になります。 さて、「3枚裏返す作業を1回とする。」とあります。3枚裏返す作業をk回行うとすると、コインは計3k回裏返ることになります。全てのコインが×になるので、4枚のコインは全て奇数回裏返された。よって、3k＝偶数ですね。
最小のkは2ということになりますが、そうはいきません。なぜならば、一つの作業で、3枚のコインを裏がえさなければならないからです。（問題文にそう書いてあります）つまり、
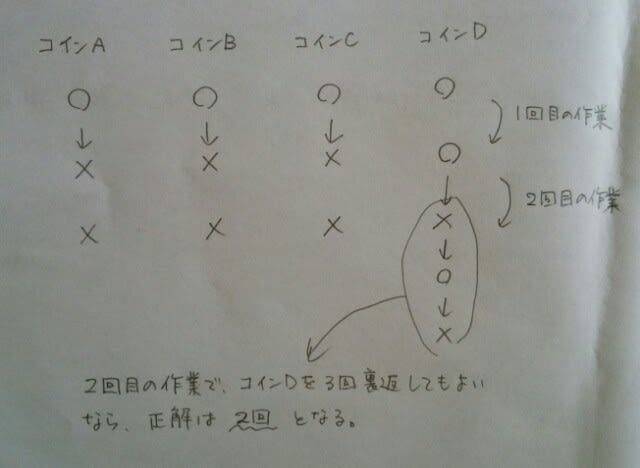とすると、k＝4が最小と思われるので、やってみたら、
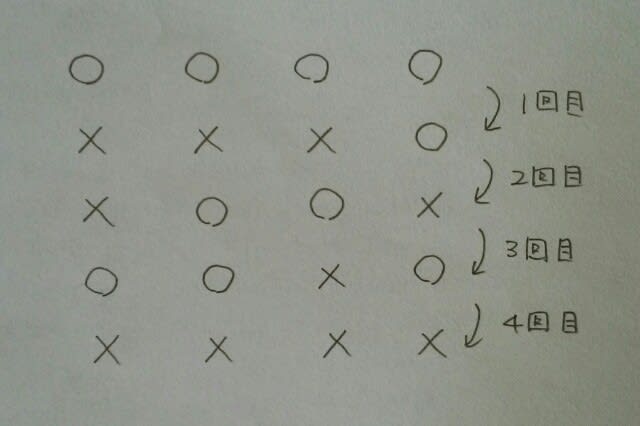できました。正解は、肢②です。ここをポチッとお願いします。→
にほんブログ村
最小のkは2ということになりますが、そうはいきません。なぜならば、一つの作業で、3枚のコインを裏がえさなければならないからです。（問題文にそう書いてあります）つまり、とすると、k＝4が最小と思われるので、やってみたら、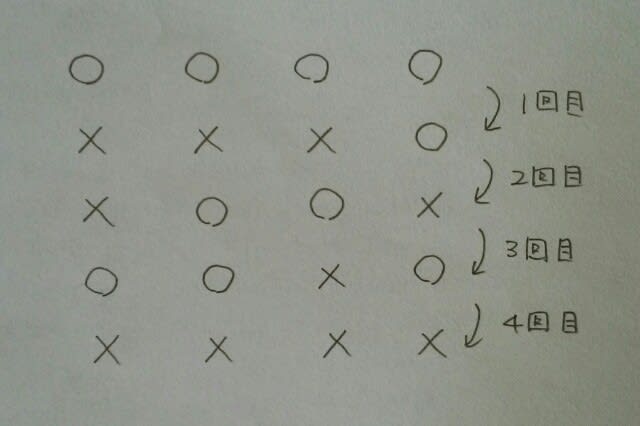できました。正解は、肢②です。ここをポチッとお願いします。→にほんブログ村
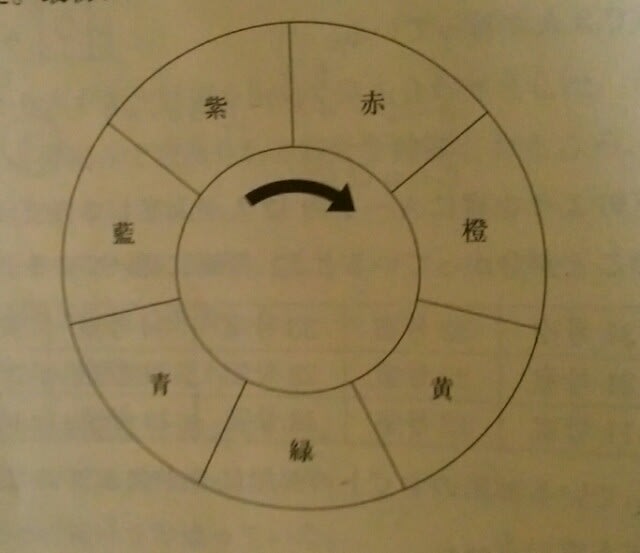①藍②紫③橙④緑⑤青 選択肢を使って、①から一つずつやれば、1、2分で答えは見つかりますが、選択肢を使わずにやってみます。 １つ目のコマが黄で、3つ目のコマが紫なので、1回目に出た目の数をa、2回目に出た目の数をbとすると、スタート地点から、aだけ進むと黄、a＋bだけ進むと紫なので、こんなイメージです。
黄から紫までは4マスなので、b＝4です。2つ目のコマは、b（＝4）だけ進むと赤に止まったのだから、スタート地点は、赤から4マス戻った緑ですね。正解は、肢④です。 念のために確かめてみます。スタート地点が緑だとすると、a＝6で、１つ目のコマは黄に来ます。b＝4だから、2つ目のコマは赤に来ます。6＋4＝10なので、確かに3つ目のコマは紫に来ます。ここをポチッとお願いします。→
東西南北のスイッチは、シャンデリア3個とスポットライト1個か、シャンデリア1個とスポットライト3個か、のどちらかです。 まあ、普通の大広間だったら、2個ずつにしてあるんだけれども、それだと東西南北のスイッチを1回ずつ押すと、どちらも（－）になってしまいますので、この大広間はおかしな大広間だなあと分かりますが。 続けて、西と南と北のスイッチを押すと、シャンデリアが点灯、スポットライト消灯なので、
さらに続けて、西と北のスイッチを押すと～。
結局、西と北は、シャンデリアとスポットライトが1個ずつ。ということは、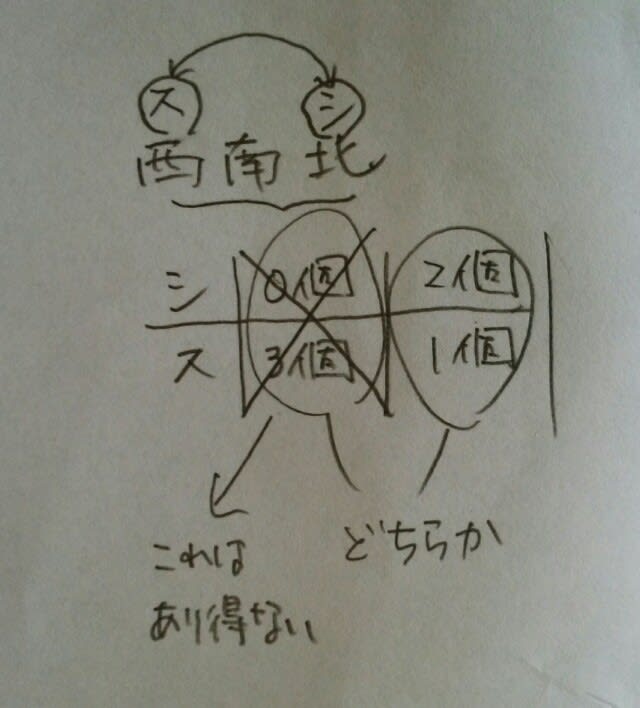
ということは、
ということは、
ということは、
ということは、正解は、肢②です。ということは、ここをポチッとお願いします。→
A君は、自分がX班になるかY班になるかが知りたくて、顧問の先生に聞きに行きました。 すると、顧問の先生は、「ああ、BとCはY班で、DはX班だよ。ただし、このことは、決してB、C、Dに言ってはならない。言ったら君には退部してもらうよ。はははのは！」 こんな顧問、殴ってやりたくなりますねぇ。次の問題では、さらにイヤらしくなりますよ。平成23年度国家Ⅰ種より。 A～Eの5人が、キャンプの班分けで自分がX班になるかY班になるかを知りたいと思い、担当の顧問に聞きにいった。すると顧問は、各人に対して個別に、本人と他の1人を除く3人についてのみ、X班かY班かを教えた。A～Eの各人が得た情報は次のとおりである。
その後、顧問は、A～Eが一堂に会した場で、○各人にどの3人の班を教えたかということ○Y班は多くとも3人であることの2点を伝えた。 その時点で、A～Eのだれも自分の班を特定できなかったが、そこでだれも自分の班を特定できないとわかると、まず1人だけが自分の班を特定することができた。それはだれか。①A②B③C④D⑤E そもそも、なぜこの人たちは、顧問の先生に聞きにいったのでしょうか？おそらく、X班は、近所のお粗末キャンプ場で、Y班はハワイのウッキウキキャンプ場で、自分がどっちになるか気になって仕方がなかったからです。ハワイに行けるのは多くとも3人までです。例えば、嫌みな顧問が、A君に、
と伝えたならば、A君は、もう諦めるしかありません。 A～Eの5人ともが自分の班を特定できなかったのですから、各人は、自分が教えてもらった3人が3人ともY班だったということはあり得ないのです。3人の中に必ずX班の人がいたのです。すると、A君は、こう考えます。 「BとCはハワイだなあ。EはボクとBとCのことを知っている。ボクとBとCは3人ともハワイに行くことはないのかあ。はあ？えええええ？じゃあボ、ボ、ボクは………😢」ということで、正解は、肢①でした。ここをポチッとお願いします。→
前回の記事の途中まで再掲します。平成17年の地方上級からです。 表に1～5の数が一つずつ書かれた5枚のカードが裏返しに置かれている。A～Cの3人がこの中から1枚ずつカードを抜き取り、手に持ったカードの表を前に向けて立った。このとき、3人はいずれも他の2人のカードは見えるが、自分のカードは見えない。3人は、自分が他の2人のカードの数よりも大きい数のカードを持っていると分かったときには「勝った」、自分のカードの数より大きい数のカードを持っている者がいると分かったときには「負けた」、どちらとも判断できないときには「分からない」と言うことにした。 3人がA、B、Cの順にそれぞれ、見えているカードとそれまでに他の者の発言があるときはその発言とから、次のように述べた。このとき、各人の持っているカードについて確実にいえるのはどれか。 A 「分からない。」 B 「分からない。」 C 「負けた。」 ①Aは4を持っている。 ②Aは5を持っている。 ③Bは4を持っている。 ④Cは1を持っている。 ⑤Cは2を持っている。 Aは、どんなときに「勝った。」と発言するでしょうか？BとCが、1と2（順不同）を持っていたときですね。（自分は必ず3以上の数を持っていることになる） 次に、Aは、どんなときに「負けた。」と発言するでしょうか？BかCが5を持っていたときですね。（自分は4以下だから） Aは、「分からない。」と発言したのだから、こういうことです。
ここで、大事なことがあります。 BもCも、Aの発言を聞いていたということです。 先ほどの表は、問題を解いている我々だけが知っていることではなく、A、B、C3人とも知っているということなのです。例えば、BもCも、自分は5のカードを持っていないと気が付いているのです。 Bは、どんなときに「勝った。」と発言するでしょうか？AとCが1と2（順不同）を持っていたときですね。 どんなときに「負けた。」と発言するでしょうか？AかCが4以上のカードを持っていたときですね。（自分は4以下だと知っているから） Bは、「分からない。」と発言したのだから、こうです。
次に発言するCは、この表のような状態であることに気が付いていますよ。Cはこう考えます。 「俺はどうせ3以下の小せえやつさ。もしもAかBが3以上のカードを持っていたら俺の負け😩。AとBが1と2（順不同）なら俺の勝ち🙌。さあ、勝負だ！」と、AとBのカードを見てみますと、「おっと、いけねえ！負けちまった～😵」ということで、AかB（または2人とも）は3か4を持っていました。ところが、Bが3を持っていたなら、
ということになり、AとCが1と2を持っていることになり、△に違反します。 ここまでは、間違ってはいませんので、ここから先を訂正します。Aが3を持っていたらどうなるでしょうか？
Bは、AとCのカードを見て、こう考えます。（例えば、Aが3で、Cが1）
「ん？Cの野郎、1だな。ほんとに小せえ奴だ。俺とCは1と2の組み合わせじゃあねえから、俺は1でも2でも3でもねえ。4だ。はっはっは。俺の勝ちじゃねえか。お～い、僕、勝ちましたよ～🙌」 Aが3でCが2だったとしても同じことですね。つまり、もしもAが3だったら、Bは「勝った。」と発言するのです。よって、Aは3ではありません。なので、Bは4です。（Cは、AとBのカードの中に、3か4があったから、「負けた。」と発言したのですから）
Aは1か2で、AとCは1と2の組み合わせではないので、Cは3です。
正解は変わらず、肢③です。まあ、許してやるよって方は、ここをポチッとお願いします。→