地方初級の数的推理 4

2021年出題。　　　　　　　　　　　　　　　　　　　　　1円玉が2枚、5円玉が4枚、10円玉が2枚の計8枚の硬貨がある。　　　　　　　　　　　　　　この中から、5枚を選んだとき、選んだ硬貨の合計金額が、残った硬貨の合計金額より大きくなる場合は何通りあるか。　　　　　　　　　　　　　　　なお、同じ金額の硬貨は区別しないものとする。（選択肢省略）　　　　　　　　　　　　　　　　　　　こういうことですね。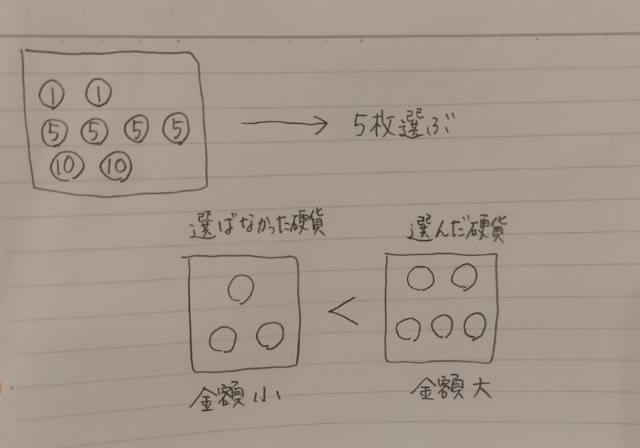
どれを選んだか?ということになれば、選んだ5枚の組み合わせを探すことになります。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　しかし、どれを選ばなかったか?ということになれば、選ばなかった3枚を探すことになりますね。　　　　　　　　　　　　　　　　　　　　　　こりゃあ、選ばなかった3枚の硬貨を探す方が楽ちん〜。　　　　　　　　　　　　　　　　　　　　　　　　8枚の硬貨の合計金額は、1×2＋5×4＋10×2＝42円。　　　　　　　　　　　　　　　　　　　　　　　　これの半分は21円ですから、選ばなかった硬貨の合計金額は210円未満、選んだ硬貨の合計金額は210円超。


3枚で210円未満になる組み合わせを探します。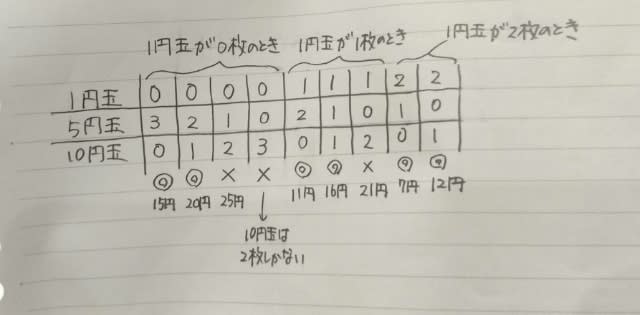　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　◎印のものが条件を満たす組み合わせです。　　　　　　　　　　　　　　　　　　　　　　　　繰り返しますが、選ばなかった3枚の硬貨が決まれば、自動的に選んだ5枚の硬貨も決まりますね。　　　　　　　　　　　　　　　　　　　以上より、正解は6通りであります。

地方初級の数的推理 3

2021年出題。　　　　　　　　　　　　　　　　　　　　　濃度11%の食塩水の入った容器に水を150g追加したところ、食塩水の濃度が5%になった。　　　　　　　　　　　　　　　　　　　　この容器に最初から入っていた食塩水は何gか。（選択肢省略）　　　　　　　　　　　　　　　　　食塩水の問題では、水＝0%、食塩＝100%です。　　　　　　　　　　　　　　　　　　　　　　　この容器に最初から入っていた食塩水の量をx（g）として、図にすると、
実は、上下を掛け合わせた方程式を解けば終わりです。
正解は、125gです。

地方初級の数的推理 2

2021年出題。　　　　　　　　　　　　　　　　　　高校3年生の理科の選択科目のうち、物理選択者は90人、生物選択者は116人である。　　　　　　　　　　　　　　　　　　　　　　　　　男女別では、生物を選択している男子は物理を選択している男子の1.2倍、生物を選択している女子は物理を選択している女子の1.4倍であった。　　　　　　　　　　　　　　　　　　このとき、物理を選択している男女の差は何人か。（選択肢省略）　　　　　　　　　　　　　　　　こんな表に整理します。
物理を選択している男子をx人、物理を選択している女子をy人として、ここに条件を記入すると、
この表から、x＋y＝90、1.2x＋1.4y＝116という連立方程式ができます。（2.2x＋2.4y＝206でも構いません）　　　　　　　　この連立方程式を解きます。
よって、物理を選択している男女の差は50−40＝10人。　　　　　　　　　　　　　　　　　　　正解は10人です。

地方初級の数的推理 1

2021年出題。　　　　　　　　　　　　　　　　　　　　　売店で40円、60円、80円の3種類のお菓子をそれぞれ1個以上、合計13個買ったところ、合計金額は720円であった。　　　　　　　　　　　60円のお菓子よりも80円のお菓子を多く買ったとすると、40円のお菓子はいくつ買ったか。　　　　　　　　　　　　　　　　　　　　　　　　　　　なお、消費税は含まないものとする。　　　　　　　　　　①3個②4個③5個④6個⑤7個　　　　　　　　　　　　　　　　　40円のお菓子をx個、60円のお菓子をy個、80円のお菓子をz個買ったとします。　　　　　　　　　　　　　　　　　　　合計13個買ったことと、合計金額が720円ということなので、次のようになります。
この表から、x＋y＋z＝13。　　　　　　　　　　　　　40x＋60y＋80z＝720という方程式ができます。
何でもいいので、何か文字を1つ減らします。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　例えば、今、xという文字を減らしてみます。（数学では、文字xを消去すると言います）
最後に出てきた、y＝10−2zと、始めにあるx＋y＋z＝13が決め手です。　　　　　　　　　　　　　　　例えば、z＝1だとしたら？
この流れは、めちゃくちゃ大事なので、スラスラいけるまで練習しなければいけません。　　　　　　　　　　　　　　　　　　　　　　　　　では、z＝2だとしたら？　　　　　　　　　　　　　　　　　次にz＝3だとしたら？　　　　　　　　　　　　　　　　　　　　　しかし、xとyとzの組み合わせが次々現れるので、何か表にまとめながらやらないと、グッチャグチャになりますね。　　　　　　　　　　　　　　そこで、先に表を作っておきましょう。　　　　　　　　　　　　　　z＝1のときの結果は書き込んでおきました。
この先を埋めて下さい。　　　　　　　　　　　　　　　　　　　こうなりますね。
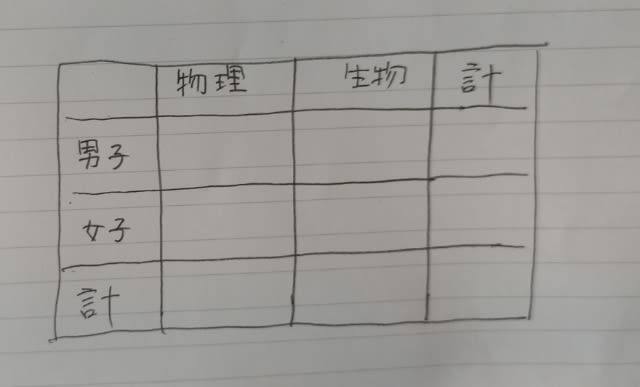
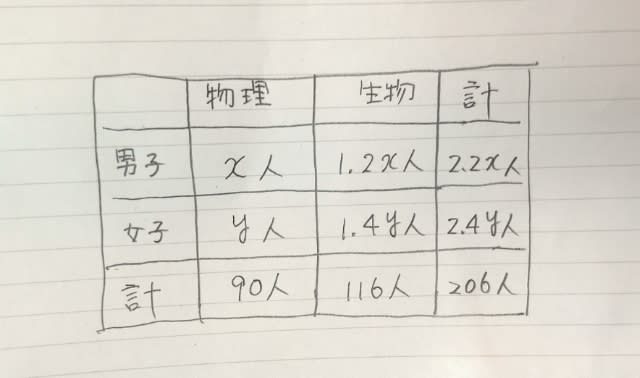
zを5以上にすると、yが0や負の数になるので、表は完成です。　　　　　　　　　　　　　　　　　　　　　でも、こんなに丁寧に計算すると、時間が‥‥😫　　　　　　　　　　　　　　　　　　　　　　　　　　なので、実際には、こうします。このように、買うお菓子の数の組み合わせは4組みつかりました。　　　　　　　　　　　　　この中で、「60円のお菓子（ここではy）よりも80円のお菓子（ここではz）を多く買ったとすると」という条件に当てはまるのは、完成した表の一番右にある、x＝7、y＝2、z＝4です。　　　　　　　　　　　　　　　　　　　　　　このとき、40円のお菓子（ここではx）は7個買っているので、正解は、肢⑤です。

地方上級の判断推理 6

2021年出題。　　　　　　　　　　　　　　　　　　　　　　ある装置Xにおいて「条件Aを満たしておらず、かつ条件Bを満たしていない場合、装置Xは稼働しない」ことがわかっている。　　　　　　　　　　　　　　　　　　　　　　　　　　そのことから論理的に言えるのはどれか。　　　　　　　　　　　　　　　　　　　　　　　　　　①装置Xが稼働する場合、条件A、Bのどちらか一方だけを満たしている。　　　　　　　　　　　　　　②装置Xが稼働する場合、条件A、Bの少なくとも一方は満たしている。　　　　　　　　　　　　　　　③装置Xが稼働しない場合、条件Aを満たしておらず、かつ条件Bも満たしていない。　　　　　　　　　　　　　　　　　　　　　　　　　　　④条件Aを満たしており、かつ条件Bを満たしている場合、装置Xは稼働する。　　　　　　　　　　　　　　　　　　　⑤条件A、Bのどちらかしか満たしていない場合、装置Xは稼働しない。　　　　　　　　　　　　　以下のように記述します。
「条件Aを満たしておらず、かつ条件Bを満たしていない場合、装置Xは稼働しない」は、次のように表されます。
これの対偶は、
矢印の右側を、ドモルガンの法則で簡単にします。ドモルガンの法則については、カテゴリーの論理に過去の記事があります。　　　　　　　　　　　　　　　　　　　　　　X→A∪Bとは、装置Xが稼働する場合、条件Aを満たしているか、または条件Bを満たしている。（どちらも満たしていてもOK）ということですから、正解は、肢②です。　　　　　　　　　　　　　　　　　　　　　　　　　しかし、他の選択肢がなぜダメなのかがハッキリしませんねえ。　　　　　　　　　　　　　　　　　これをハッキリさせるには、これも過去記事ですが、カテゴリーの論理の予想問題（論理）や、新潟県教員採用試験no7（2015.7.5）で紹介している方法をとります。　　　　　　　　　　　　　　　　　　　　　　　　　つまり、
「条件Aを満たしておらず、かつ条件Bを満たしていない場合、装置Xは稼働しない」ということは、
肢①‥‥アのように、装置Xが稼働する場合、条件A、Bの両方満たしていることがあり得る。　　　　　　　　　　　　　　　　　　　　　肢③‥‥エやオやカのように、装置Xが稼働しない場合、条件A、B両方満たしていたり、条件A、Bのうちどちらか一方だけ満たしていることもあり得る。　　　　　　　　　　　　　　肢④‥‥エのように、条件Aを満たしており、かつ条件Bを満たしている場合に、装置Xが稼働しないときもあり得る。　　　　　　　　　　　　　　肢⑤‥‥イやウのように、条件A、Bのどちらかしか満たしていなくても、装置Xが稼働することがある。