箱の中に何本かの缶ジュースがあり、A~Eの5人で分けた。次のことが分かっているとき、DとEに分けられた缶ジュースの本数の合計は何本か。 ◯AとBに分けられた缶ジュースの本数の合計は、分ける前の本数の7/18である。 ◯AとCに分けられた缶ジュースの本数の合計は、分ける前の本数の4/9である。 ◯BとCに分けられた缶ジュースの本数の合計は、分ける前の本数の1/3である。 ◯Aが自分に分けられた缶ジュースをBに4本渡したところ、AとBの缶ジュースの本数は等しくなった。 ①26本 ②28本 ③30本 ④32本 ⑤34本 「分ける前の缶ジュースの本数は100本だ」という人がいたら、その人は嘘つきです。 なぜならば、100本の7/18などないからです。 つまり、はじめの条件から、分ける前の本数は、18の倍数だと分かります。 二つ目の条件からは、分ける前の本数が9の倍数だと分かり、三つ目の条件からは、分ける前の本数が3の倍数だと分かります。 18と9と3の最小公倍数は18なので、分ける前の本数を18k本とします。すると、
ゆえに、
DとEの合計は、7.5の倍数なので、選択肢上、正解は③しかありません。 選択肢なしでやってみましょう。
ここで、最後の条件より、
ってな寸法です。 ここをポチッとお願いします。→" "
" "
"
にほんブログ村"

ゆえに、

DとEの合計は、7.5の倍数なので、選択肢上、正解は③しかありません。 選択肢なしでやってみましょう。

ここで、最後の条件より、

ってな寸法です。 ここをポチッとお願いします。→"
 "
"
にほんブログ村"
正三角形、正方形、ひし形、正五角形、長方形の図形がある。3つの角が、30º、60º、90ºの合同な2つの直角三角形を、長さの同じ辺をきちんとあわせてつくることができる図形を全て選んでいるのはどれか。①~⑤から一つ選んで番号で答えなさい。①正方形、ひし形②正三角形、正方形、正五角形③正方形、長方形④正三角形、長方形⑤正三角形、ひし形、長方形 正三角形は、こうするとできます。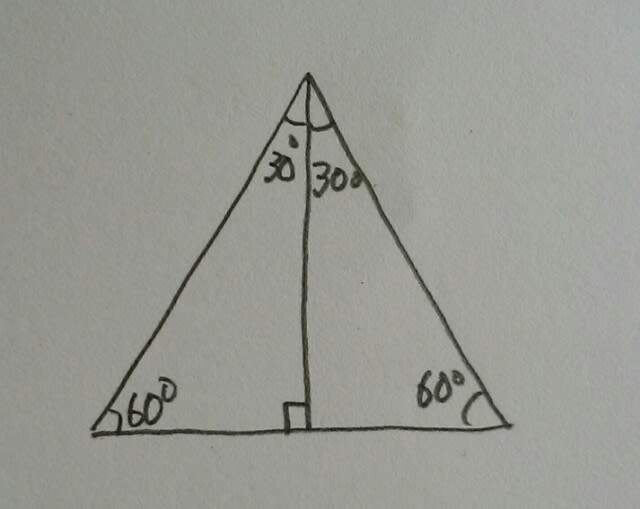 とすると、ほぼ必然的にひし形もできま~す。
とすると、ほぼ必然的にひし形もできま~す。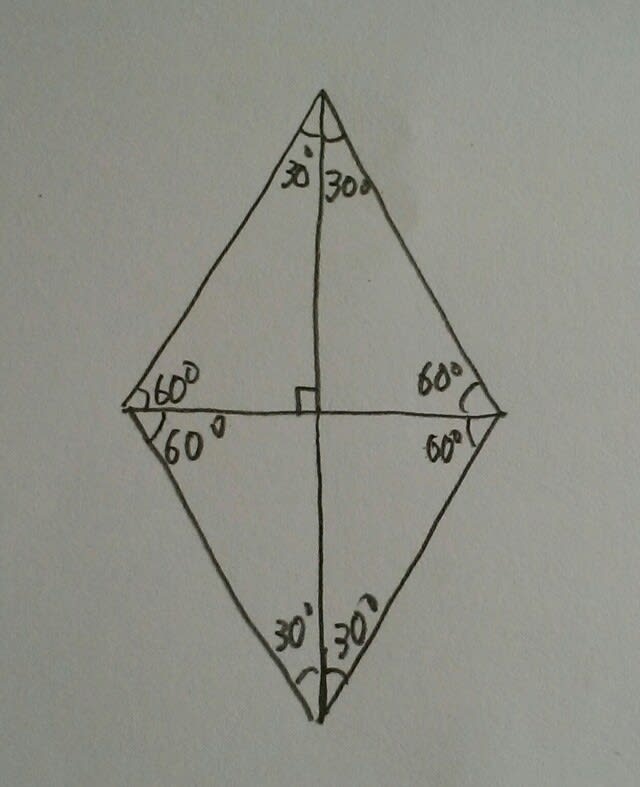 あとはどうでしょうか?「長さの同じ辺をきちんとあわせて」と書いてありますから、例えば、斜辺どうしを合わせて、
あとはどうでしょうか?「長さの同じ辺をきちんとあわせて」と書いてありますから、例えば、斜辺どうしを合わせて、 長方形もできま~す。 おお~っと、😨「2つの直角三角形を」と書いてありますから、ひし形はできませ~ん。いちばん短い辺どうしを合わせて、
長方形もできま~す。 おお~っと、😨「2つの直角三角形を」と書いてありますから、ひし形はできませ~ん。いちばん短い辺どうしを合わせて、 二等辺三角形はできま~す。 でもそんな選択肢はありませ~ん。 正方形、正五角形は、できるわけありません。 正解は、肢④です。ここをポチッとお願いします。→
二等辺三角形はできま~す。 でもそんな選択肢はありませ~ん。 正方形、正五角形は、できるわけありません。 正解は、肢④です。ここをポチッとお願いします。→
にほんブログ村

 とすると、ほぼ必然的にひし形もできま~す。
とすると、ほぼ必然的にひし形もできま~す。 あとはどうでしょうか?「長さの同じ辺をきちんとあわせて」と書いてありますから、例えば、斜辺どうしを合わせて、
あとはどうでしょうか?「長さの同じ辺をきちんとあわせて」と書いてありますから、例えば、斜辺どうしを合わせて、 長方形もできま~す。 おお~っと、😨「2つの直角三角形を」と書いてありますから、ひし形はできませ~ん。いちばん短い辺どうしを合わせて、
長方形もできま~す。 おお~っと、😨「2つの直角三角形を」と書いてありますから、ひし形はできませ~ん。いちばん短い辺どうしを合わせて、 二等辺三角形はできま~す。 でもそんな選択肢はありませ~ん。 正方形、正五角形は、できるわけありません。 正解は、肢④です。ここをポチッとお願いします。→
二等辺三角形はできま~す。 でもそんな選択肢はありませ~ん。 正方形、正五角形は、できるわけありません。 正解は、肢④です。ここをポチッとお願いします。→にほんブログ村
















