対称式に限らず、類似問題を紹介します。 ☆長野県教員採用試験より。
前回紹介した、出題パターン②の、何でもかんでも代入というのを封じるやつです。xとyの値が出ていませんので、ややもすると、こうなってしまいますね。
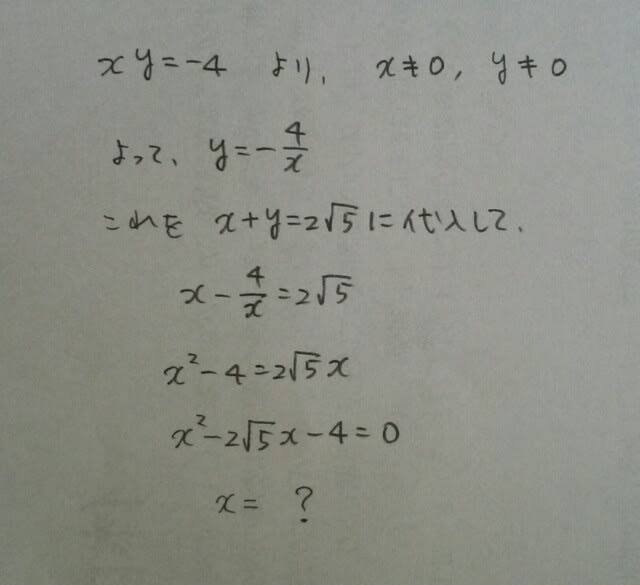なので、こうです。
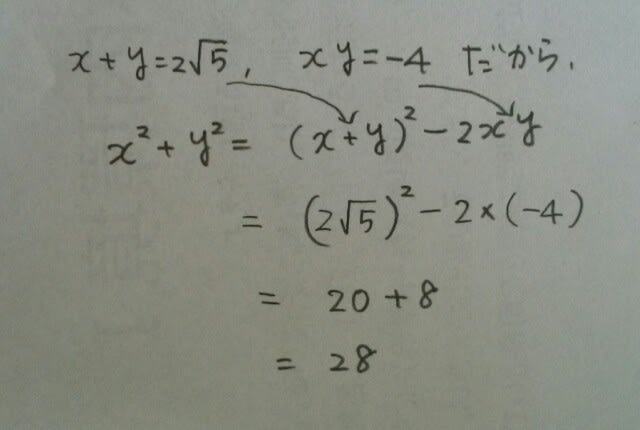正解は、肢⑤です。 ☆埼玉県教員採用試験小学全科より。
直接代入でも構いませんが、計算が面倒です。ここで出てきた式は、対称式ではありません。（xとyを入れかえると違う式になります）だから、あまり形にとらわれずに、こうしましょう。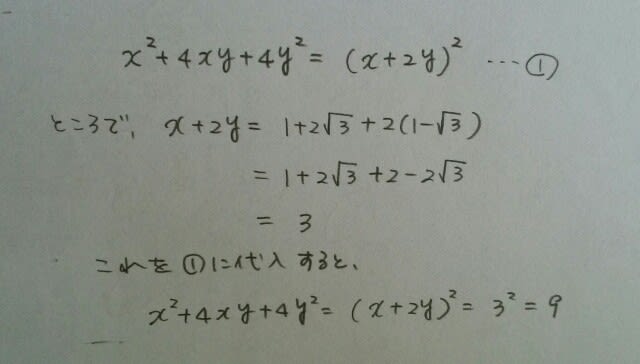
正解は、肢1です。最後に上級者向けです。 ☆高知県教員採用試験小学全科より。
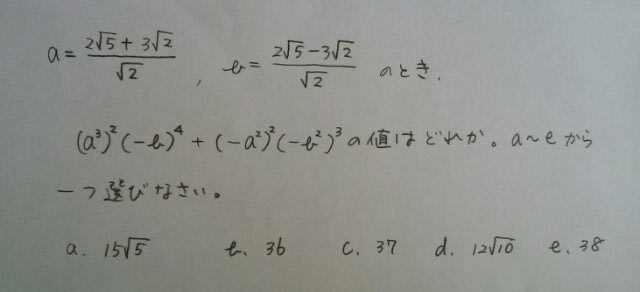正解は、動物画像の下です。皆さん、よいお年をお迎え下さい。ここをポチッとお願いします。→
にほんブログ村
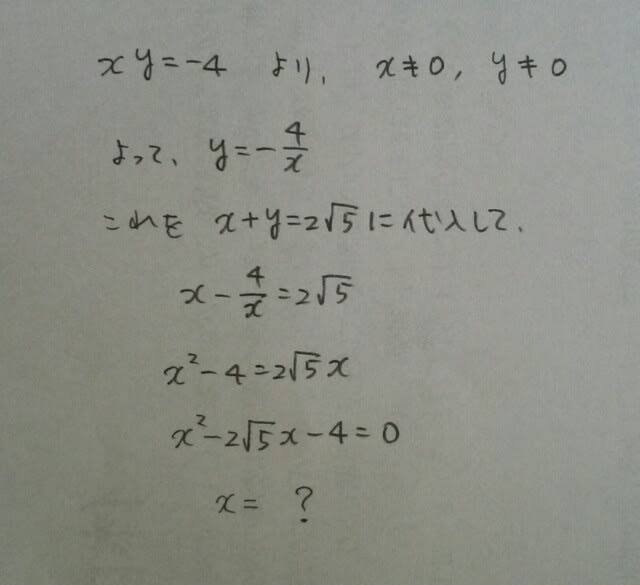前回紹介した、出題パターン②の、何でもかんでも代入というのを封じるやつです。xとyの値が出ていませんので、ややもすると、こうなってしまいますね。なので、こうです。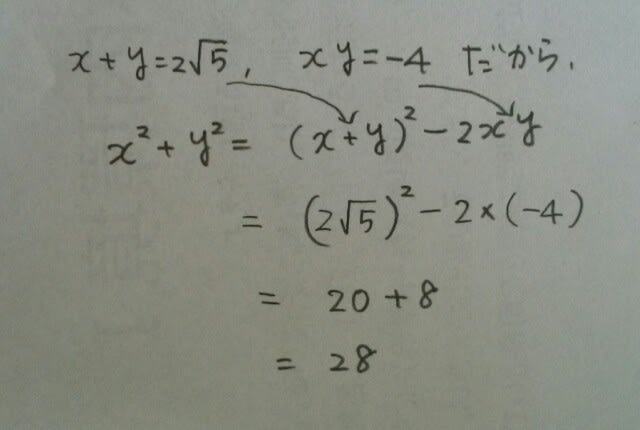正解は、肢⑤です。 ☆埼玉県教員採用試験小学全科より。直接代入でも構いませんが、計算が面倒です。ここで出てきた式は、対称式ではありません。（xとyを入れかえると違う式になります）だから、あまり形にとらわれずに、こうしましょう。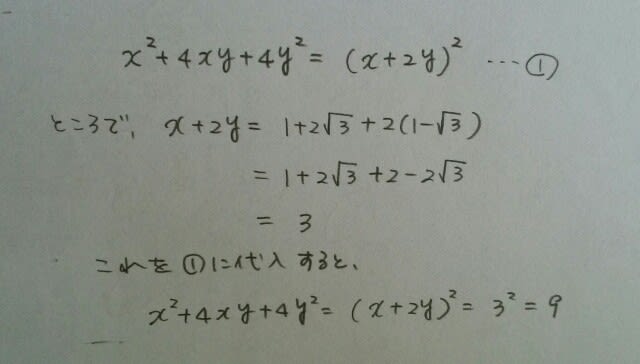正解は、肢1です。最後に上級者向けです。 ☆高知県教員採用試験小学全科より。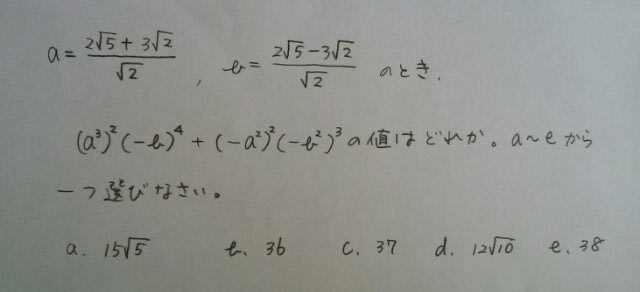正解は、動物画像の下です。皆さん、よいお年をお迎え下さい。ここをポチッとお願いします。→
にほんブログ村
定義は難しいので知らなくてもいいのですが、簡単にいうと、「xとyを入れかえても変わらない式」を対称式といいます。教員採用試験の教養では頻出です。 出題パターンは、ほとんど次の2つです。①x＝☆、y＝♡のとき、対称式（例えばx2乗＋y2乗）の値を求めよ。 ②x＋y＝☆、xy＝♡のとき、対称式の値を求めよ。 ②は、何でもかんでも代入してというやり方を封じる問題です。まず、問1です。山梨県教員採用試験小学全科より。
対称式の値を求めるときの手順は、 その1 x＋yと、xyの値を求める。 その2 対称式を変形する。 その3 変形した式に、その1で求めた値を代入する、です。 手順通りにやってみますと、
まあ、これでいいのですが、何か、堅苦しいというか、窮屈というか……。実は、この窮屈さが大事と言えば大事なことであるような、ないような……。つまり、直接代入してもいいじゃないかっと。
もちろん、これでも構いません。形ばかりに囚われていると失敗するのが数学ですから、こういうのもあるなあというのは大事です。 次に、対称式を変形するときのポイントです。よく使うのが、
この3つです。意味は、こうです。
暗記しなくても、自分で導き出せそうですし、問題を解いているうちに勝手に覚えてしまいます。では、もう1問。長野県教員採用試験小学全科より。
公式にこだわってみると、
いやあ～、公式は堅苦しいので性に合わねえや！というなら、
はたまた、xとyの値を、直接代入しても構いませんし。とにかく、正解は、－6です。次回は、対称式にこだわらず、類似問題をやってみます。ここをポチッとお願いします。→
図のように家具等（タンス、戸棚、洗濯桶、ベッド、テーブル、柱時計、暖炉）が配置されている2部屋から成る家で、7匹の子ヤギの兄弟が暮らしている。 ある日、この家にオオカミがやって来たので、7匹の子ヤギの兄弟は家具等に隠れたが、うち6匹はオオカミに見つかってしまった。次のことが分かっているとき、確実にいえるのはどれか。 
○2部屋に共通して置かれている家具等のそれぞれについて、一方の部屋の家具等に子ヤギが隠れている場合は、もう一方の部屋の家具等に子ヤギは隠れていなかった。 ○長男は、テーブルの下に隠れた。 ○次男は、東側の部屋で隠れた。 ○三男と四男は、それぞれ別の部屋で隠れた。 ○五男は、テーブルよりも南側にある家具等に隠れた。 ○末っ子は、柱時計に隠れており、オオカミには見つからなかった。 ○オオカミは、西側の部屋で4匹の子ヤギを、東側の部屋で2匹の子ヤギを見つけた。 
東側の2匹は②と（③か④）なので、それ以外は全て西側ですね。
①は、西側で、テーブルの下（2つ目の条件）。⑤は、西側で、柱時計か暖炉（5つ目の条件）。でも、もしも柱時計だったら、⑦は、どこにも隠れることができません（1つ目と6つ目の条件）。よって、⑤は、西側の暖炉。
実は、はっきり決まるのはこれだけです。よって、正解は、肢4です。因みに、肢1…長男は、西側のテーブルの下です。肢2…次男は、東側の部屋のどこに隠れたか不明。肢3…三男と四男は、どちらが東側でどちらが西側か不明。肢5…末っ子は、確かに柱時計に隠れたのですが、それが東側か西側かは不明です。ここをポチッとお願いします。→
ある水そうには、A、B、Cの3つの水道管がついている。AとBの両方の水道管を同時に使って水を入れると30分でいっぱいになり、BとCの両方の水道管を同時に使って水を入れると25分でいっぱいになる。Aの水道管で1時間10分入れた後、Cの水道管で40分入れてもいっぱいになる。AとCの両方の水道管を同時に使って水をいっぱいにするには何分かかるか、①～⑤から一つ選んで番号で答えなさい。 ①35分②40分③45分④50分⑤55分（京都市教員採用試験、小学全科） 一応、水槽がいっぱいになるまでの時間は出ているのですが……。
これだけでは、Aが1分でどれだけか？Cが1分でどれだけか？AとCでは1分でどれだけか？全然分かりません。よって、ここで手詰まりです。こんな時は、こうしましょう。Aは、1分で1水が出る。Bは、1分でb、Cは1分でc水が出る、として、連立方程式を作るのです。
以上の連立方程式を解くと、b＝4、c＝2になります。計算の一例。
例えば、③の方程式を使うと、満水＝70＋40×2＝150。AとCを使うと1分で1＋2＝3ですから、150÷3＝50分で満水になりますね。正解は、肢④です。ここをポチッとお願いします。→
富山県教員採用試験より。 ある仕事をA、B、Cの3人で行うと6日間かかる。この仕事をAだけで行うと12日かかり、Bだけで行うと18日間かかる。この仕事をCだけで行うと何日かかるか求めよ。 6と12と18の最小公倍数は36ですから、仕事の量を36とします。A、B、Cの3人でやると、36の仕事を6日間でやるので、1日で6。Aだけだと12日かかるので、1日で3。Bだけだと、18日かかるので、1日で2。
Aが1日で3、Bが1日で2、AとBとCでは1日で6だから、Cは1日で1ですね。
よって、Cだけで行うと、36÷1＝36で、36日かかります。正解は、36日です。 次回は、最小公倍数ではできない仕事算を取り上げてみます。 ここをポチッとお願いします。→